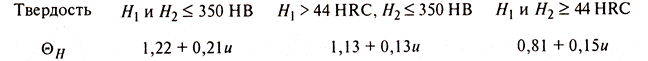ПОЗНАВАТЕЛЬНОЕ

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Занятие 5m. Расчет конических колес с круговым зубом.

Содержание:

4.1 Расчет геометрических параметров

4.2 Определение сил в зацеплении

4.3 Проверочный расчет на контактную усталость

4.4 Проверочный расчет на изгибную прочность

4.5 Проверка зубчатых колес на статическую прочность при нагружении пиковыми моментами

Детали машин и основы конструирования: Учеб./ А. Т. Скойбеда, А. В. Кузьмин, Н. Н. Макейчик; Под общ. ред. А. Т. Скойбеды. – Мн.: Выш. шк., 2006. – 559с.; ил (стр.248-269)

Рассмотрим ортогональные передачи с межосевым углом Σ=δ₁+δ₂=90º

ГОСТ 16530-83. Передачи зубчатые. Термины.

ГОСТ 19325-73.Передачи зубчатые конические. Термины, определения и обозначения.

ГОСТ 19326-73. Передачи зубчатые конические с круговыми зубьями. Расчет геометрии.

Минимально допустимое число зубьев ортогональной конической передачи:

Z₁
Z₂

Рекомендуемые передаточные числа: 1; 1,12;1,25;1,4;1,6; 1,8;2,0;2,5; 3,15;4,0; 5,0

ГОСТ 21354-87. Передачи зубчатые цилиндрические эвольвентные внешнего зацепления. Расчет на прочность.

ГОСТ 13754-81.Передачи конические с круговым зубом. Исходный контур.

α=20º; h_a^*=1; h_f^*=1,25; h_e^*=2,08; h_w^*=2,0; ρ_f^*=0,25;с^*=0,25.

ГОСТ 1758-81.Показатели точности.

Форма зуба - пропорционально понижающиеся зубья. Вершины делительного конуса и конуса впадин совпадают. Высота ножки зуба понижается пропорционально конусному расстоянию. Применяется в основном для прямозубых колес и колес с круговым зубом (z_Σ =20…100; m_n >2мм). Угол наклона линии зуба β_n=35º(предпочтительное), парные колеса имеют разное направление линий зубьев. Рекомендуется у шестерни задавать правое направление, а у колеса - левое.

По ГОСТ 19326-73 рекомендуемый ряд β_n: 0;10;15;20;25;30;35;40;45.

4.1 Расчет основных геометрических параметров (проектировочный)

4.1.1 Для проектировочного расчета вычисляем средний делительный диаметр шестерни

Где d_m₁, мм – средний делительный диаметр;

К_d = 600 МПа^1/3- вспомогательный коэффициент;

[σ_Н1], МПа – допускаемое контактное напряжение шестерни;

U- передаточное число;

Т₁, Н·м – крутящий момент на валу шестерни

4.1.1.1 Коэффициент вида конических передач, зависящий от передаточного числа и прирабатываемости зубьев, стр.265

4.1.1.2 Коэффициент ширины шестерни, относительно среднего диаметра (меньшие значения для твердых ЗК, Н1>350 НВ и Н2>350 НВ), стр.265

Ψ_вd1=(0,3…0, 6)

4.1.1.3 Коэффициент ширины зубчатого венца. Относительно конусного расстояния (формула профессора Кудрявцева)

К_ве =2·ν/(U+ν)

Где ν=0,6 – консольное расположение шестерни

ν=0,8 –расположение шестерни между двух опор

4.1.1.4 Коэффициент, учитывающий неравномерность распределения нагрузки, по номограмме в зависимости от параметра: [К_ве· U/(2- К_ве)], K_Hβ = (1…1,6), стр. 263