 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Результаты представим в виде таблицы №5
F(0)=0,83 F(2,4)=0,99 F(-2,4)=0,5 F(4,7)=0,94 F(-4,7)=0,15
F(1,1)=0,93 F(-1,1)=0,68 F(3,5)=0,98 F(-3,5)=0,34 F(5,3)=0,9 F(-5,3)=0,8
Fз(gmin1)= 0,83 Fз(gmin2)=0,94 Fз(gmin3)=0,79 Fз(gmax1)=1,61 Fз(gmax2)=1,32 Fз(gmax3)=1
Используя рассчитанные точки Fз(gmin) и Fз(gmax) строим диаграмму направленности антенны в вертикальной плоскости с учетом влияния Земли (рис. 2). Таблица № 5:
Задание 4:Определить максимальную дальность действия для свободного пространства. Максимальная дальность действия для свободного пространства рассчитывается по основному уравнению радиолокации:
Где: Ри – излучаемая мощность в импульсе; Ри = 500 к Вт; Рпр.min – чувствительность приемника; Рпр.min = σ – эффективная площадь рассеяния цели; σ = 50 м²; D – коэффициент направленного действия антенны; D = 2000; λ – длина волны; λ = 0,25 м. Подставив значения в формулу получим:
Задание 5:Построить зону обзора станции в вертикальной плоскости в прямоугольной системе координат высота – дальность. Для построения зоны радиолокатора в вертикальной плоскости надо изобразить прямоугольную систему координат высота – дальность. Для этого рассчитаем линии равных высот по формуле:
Hпр – приведенная высота H – действительная высота над поверхностью земли; r – наклонная дальность Rэ – эквивалентный радиус Земли , Rэ = 8500 км. Найдем наклонную дальность, при которой приведенная высота была бы равна нулю, то есть Нпр = 0 и формула (9) примет вид:
Линии равных высот рассчитаем для высот от 0 до 10 км через 2000м и далее для высот 20км, 30км.
Таблица №6:
Наклонную дальность r при расчете будем измерять для каждого значения Н от 0 до величины (1,2 – 1,3)rmaxсв., т.е. r = 1,61 ×354 = 569,9 км, через каждые 50 км или такого значения r при котором Нпр достигает нуля. Рассчитаем линии равных высот по формуле (9) и полученные результаты запишем в виде таблицы 6: Пример расчета: Для высоты Н = 2000м. r =50 км; r =100 км; r =150 км; По таблице №6 наносим рассчитанные точки Нпр и r на прямоугольную систему координат, откладывая по горизонтальной оси величины r, а по вертикальной Нпр. Соединяем их, и проводим линии равных высот, являющиеся параболами и линии равных расстояний, параллельные вертикальной оси. На этом же графике проводим линии равных углов места g через 0,5° от 0° до 5°, через 1° от 5° до10°, для углов 15° и 20° и далее через каждые 10°. Линии равных углов места являются прямыми проходящими через начало координат и точки с координатами (r,Hпр), где Нпр = r×sing (10). Произведем расчеты по формуле (10), подставляя указанные ранее значения g. Полученные результаты запишем в виде таблицы №7 при r = 100 км от 0° до 10° , r =50 км 15° до 30°.
Таблица №7:
По данным таблицы строим линии равных углов места. Рассчитаем точки максимальных дальностей для различных углов места по формуле:
rmax (g) = rmaxсв.Fз(g)
Величины Fз(g) будем снимать с заранее построенного графика (рис. 2). Полученные результаты запишем в виде таблицы №8 (rmax = 206 км) Таблица №8:
Наносим точки на линии равных углов места и соединяем их, получим график зоны обзора РЛС в вертикальной плоскости. Задание 6:Определить максимальную дальность действия станции на высотах:1000, 2000, 3000, 5000, 10000 м. Определим максимальную дальность действия станции на высотах: 1000, 2000, 3000, 5000, 10000 м, для этого используем рис.3. Запишем результаты в виде таблицы №9. Таблица №9:
|





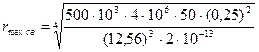 = 354 км
= 354 км (9)
(9)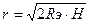
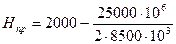 = 1853 м
= 1853 м = 1412 м
= 1412 м = 676 м
= 676 м