ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Задание 2: Рассчитать и построить диаграмму направленности антенны в горизонтальной плоскости, определить ее ширину.
Диаграмма направленности РЛС в горизонтальной плоскости рассчитывается в соответствии с выражением:
d – горизонтальный размер антенны; d = 12м. l - длина волны; l =0,25м. q° - угол в горизонтальной плоскости, отсчитываемый от оси антенны. Диаграмма является симметричной относительно направления q = 0°, а главный лепесток расположен между направлениями, лежащими по обе стороны от направления q = 0°, в которых функция F(q) первый раз достигает нулевого значения. Определим точку перехода функции F(q) через 0, то есть F(q) = 0. Тогда выражение (1) примет вид:
Правая часть этого уравнения будет равной 0 в том случае, когда 0 будет равен числитель, т.е.:
Решая последнее уравнение, получим:
pd/l × q = 0 ± pn где: n = 0,1,2,3,… Из этого уравнения
Рассчитаем диаграмму направленности в пределах главного лепестка в 12 точках. Полученные результаты представим в виде таблицы №1.
Таблица №1:
По данным таблицы №1 строим диаграмму направленности антенны в горизонтальной плоскости (рис.1). Определим ширину диаграммы направленности при F(q) = 7,07. Ширина ДНА – q = 0,72°.
Задание 3: Рассчитать и построить диаграмму направленности антенны в вертикальной плоскости для свободного пространства и с учетом влияния Земли.
Диаграмма направленности антенны в вертикальной плоскости для свободного пространства задается формулами:
Где: K – постоянный коэффициент, заданный в таблице ; К = 20 g - угол места; gо – угол места максимума диаграммы направленности; gо = 3º g1 – угол места с которого начинается косеканский закон изменения диаграммы направленности; g1 = 5º g2=35°– угол места, ограничивающий зону действия вертикальной плоскости сверху. Рассчитаем диаграмму:
Полученные результаты запишем в виде таблицы №2.
Таблица №2:
Рассчитаем диаграмму F(g) для 13-ти промежуточных точек в пределах 5° < g < 35° по формуле (3) и полученные результаты запишем в виде таблицы № 3.
Таблица №3:
По данным таблиц № 2 и № 3 строим диаграмму направленности антенны в вертикальной плоскости для свободного пространства (рис. 2). Расчет диаграммы направленности антенны в вертикальной плоскости с учетом влияния Земли С учетом влияния Земли расчет производится по формулам: F(gmin) = F (gmin) - F (- gmin) (4) F(gmax) = F (gmax) + F (- gmax) (5) Для этого сначала определим углы, при которых диаграмма направленности антенны достигает минимальных и максимальных значений, воспользовавшись формулами:
где: ha = 3 м - высота подвеса антенны; l = 0,25 м – длина волны; n = 0, 1, 2,3 … Определим предел: 0º до Получили предел 0°£ g £ 6°. По формулам рассчитаем углы gmin и gmax в полученном пределе. Результаты запишем в таблицу № 4. n = 0, gmin = arcsin0 Þ gmin = 0° n = 1, gmin = 2,4° n = 2, gmin =4,7° n = 3, gmin =7,1°- не входит в предел
n = 0, gmax = 1,1° n = 1, gmax = 3,5 n = 2, gmax = 5,3°
Таблица № 4:
Используя данные значения, рассчитываем F(gmin), F(-gmin), F(gmax), F(-gmax), используя график диаграммы направленности антенны (рис. 2). Далее рассчитываем график диаграммы направленности с учетом влияния земли по формулам (4) и (5). |



 где:
где:



 Главный лепесток диаграммы направленности находится в пределах от -1,194° до +1,194°.
Главный лепесток диаграммы направленности находится в пределах от -1,194° до +1,194°. = 0,98
= 0,98 =0,95
=0,95 = 0,89
= 0,89 =0,82
=0,82 =0,73
=0,73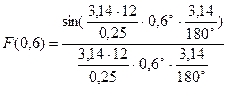 =0,63
=0,63 =0,52
=0,52 =0,41
=0,41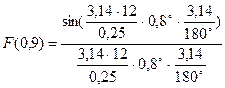 =0,29
=0,29 =0,18
=0,18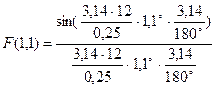 =0,08
=0,08 =0,003
=0,003 для
для  (2)
(2) для
для  (3)
(3) g Þ -6° £ g £ 5° , по формуле (2)
g Þ -6° £ g £ 5° , по формуле (2)
 , откуда
, откуда 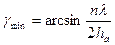 (6)
(6)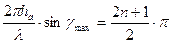 , откуда
, откуда 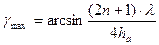 (7)
(7)