 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Дифференциальное исчисление функций многих переменных. 12
Функции нескольких переменных. Область определения. Предел функции. Непрерывность. Частные производные. Полный дифференциал. Касательная плоскость и нормаль к поверхности. Производная в данном направлении и градиент функции. Частные производные высших порядков. Экстремумы функции нескольких переменных. Необходимое и достаточные условия экстремума. Задание 1. ОПРЕДЕЛИТЕЛИ. Вычислить определитель двумя способами. Вариант 1. 1.1 Вариант 4. 1.1
Вариант 7. 1.1 Вариант 10. 1.1 1.2. Найти миноры и алгебраические дополнения определители для элементов: Вариант 1.2.1.1.
Вариант 2.2.1. Вариант 3. 2.1. Вариант 4.2.1. Вариант 5.2.1. Вариант 6. Вариант 7. Вариант 8. Вариант 9. Вариант 10. Задание 2. Матрицы. Вычислить 3А – 2В + АВ В.1 В.3 В.5 В.7 В.9 Задание 3. СИСТЕМЫ УРАВНЕНИЙ. 1. Решить систему методом Крамера и проверить методом Гаусса. 2. Решить систему с помощью обратной матрицы.
В-1 3.1 В-2 3.1 В-3 3.1 В-4 3.1
В-53.1
В-73.1 В-93.1 Задание 4. ПРЯМАЯ НА ПЛОСКОСТИ В 1.Построить чертеж. 4. Составить уравнение прямой ВN // АС. 5. Составить уравнение медианы СД. 6. Уравнение высоты АЕ, найти ее длину. 7. Найти углы треугольника. 8. Найти координаты центра тяжести.
Задание 5. ПРЯМАЯ И ПЛОСКОСТЬ. Даны координаты вершин пирамиды А 1) длину ребра А 3) площадь грани А 4) уравнение прямой А 7) угол между ребром А
Задание 6. КРИВЫЕ ВТОРОГО ПОРЯДКА. 1.Найти координаты вершины и фокусов параболы, составить уравнения оси и директрисы параболы Вариант 1.а/ у2-6у-12х-15=0, б/ х2-4х-16у+52=0. Вариант 2. а/ х2-2х-12у+13=0, б/ у2-4у-12х+16=0. Вариант 3. а/ у2+6у-8х+1=0, б/ х2+6х-12у+21=0 Вариант 4. а/ х2+2х-20у-79=0, б/ у2-4у+8х-12=0. Вариант 5.а/ у2-4у-16х+52=0, б/ х2+8х-28у+44=0. Вариант 6.а/х2+8х+16у +48=0, б/ у2-4у-24х+28=0. Вариант 7.а/ х2-6х-12у-15=0, б/ у2-4у-16х+52=0. Вариант 8.а/ у2-2у-12х+13=0, б/ х2-4х-12у+16=0. Вариант 9.а/ у2+6х-8у+1=0, б/ х2+6у-12х+21=0. Вариант 10.а/ у2+2у-20х-79=0, б/ х2-4х+8у-12=0. Построить кривые по данным уравнениям:
Задание 7. Предел функции. 7.1. Вычислить предел функции при х В-1. f(x) = Вариант 2. f(x) = Вариант 3. f(x) = Вариант 4. f(x) = Вариант 5. f(x) = Вариант 6. f(x) = Вариант 7. f(x) = Вариант 8. f(x) = Вариант 9. f(x) = Вариант 10. f(x) = 7.2. Вычислить предел функции при х В-1. f(x) = В-7. f(x) = В-9. f(x) = 7.3. Вычислить предел функции при х В-1. f(x) = В-6. f(x) = 7.4. Вычислить предел функции при х В -1. f (x) = В -5. f (x) = В -9. f (x) = Задание 8. Найти производные функций: В – 1.а)у = В – 2.а)у = В – 3.а)у = В – 4.а)у = В – 5.а)у = В – 6.а)у = В –7.а)у = В – 8.а)у = В – 9.а)у = В – 10.а)у = 12 |




 Вариант 2. 1.1
Вариант 2. 1.1  Вариант 3. 1.1
Вариант 3. 1.1 
 Вариант 5. 1.1
Вариант 5. 1.1  Вариант 6. 1.1
Вариант 6. 1.1 

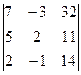 Вариант 8. 1.1
Вариант 8. 1.1 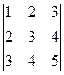 Вариант 9. 1.1
Вариант 9. 1.1 

 определителя
определителя  1.2.2
1.2.2 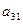 определителя
определителя
 определителя
определителя  2.2.
2.2.  определителя
определителя
 2.2 .
2.2 . 
 определителя
определителя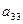 определителя
определителя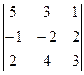
 определителя
определителя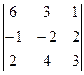

 ,
, 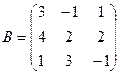 В.2
В.2 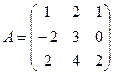 ,
, 
 ,
,  В.4
В.4  ,
, 
 ,
,  В.6
В.6  ,
, 
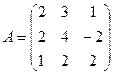 ,
,  В.8
В.8  ,
, 
 ,
,  В.10
В.10  ,
, 
 3.2
3.2 
 3.2
3.2 
 3.2
3.2 
 3.2
3.2  3.2
3.2  В-63.1
В-63.1  3.2
3.2 
 3.2
3.2  В-83.1
В-83.1  3.2
3.2 
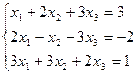 3.2
3.2  В-103.1
В-103.1  3.2
3.2 
 АВС даны координаты вершин.
АВС даны координаты вершин. А
А  А
А  А
А  . Найти:
. Найти: А
А  А
А  +(у-3)
+(у-3)  ,
, 
 ,
, 
 ,
, 
 ,
, 
 ,
, 
 ,
, 
 ,
, 
 ,
, 
 ,
, 
 ,
, 
 х
х  :
: а) х
а) х  .
. а) х
а) х  а) х
а) х  а) х
а) х  а) х
а) х  а) х
а) х  а) х
а) х 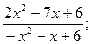 а) х
а) х  а) х
а) х  а) х
а) х  х
х  х
х  х
х  х
х  х
х  х
х  х
х  х
х  х
х  х
х  В-2. f(x) =
В-2. f(x) =  В-3. f(x) =
В-3. f(x) = 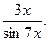 В-4. f(x) =
В-4. f(x) =  В-5. f(x) =
В-5. f(x) = 
 В-7. f(x) = 3x·ctg5x. В-8. f(x) = 4x·ctg6x В-9. f(x) = x·ctg3x. В-10. f(x) =
В-7. f(x) = 3x·ctg5x. В-8. f(x) = 4x·ctg6x В-9. f(x) = x·ctg3x. В-10. f(x) = 
 В - 2. f (x) =
В - 2. f (x) =  В-3. f (x) =
В-3. f (x) = 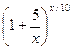 В - 4. f (x) =
В - 4. f (x) = 
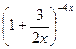 В- 6. f (x) =
В- 6. f (x) =  В-7.f (x) =
В-7.f (x) =  В-8. f (x) =
В-8. f (x) = 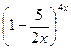
 В - 10. f (x) =
В - 10. f (x) = 
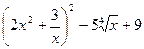 , б) у =
, б) у =  , в) у = sin 3x · e
, в) у = sin 3x · e  , г) y = arctg ln 2x.
, г) y = arctg ln 2x. , б) у =
, б) у =  , в) у = ctg 4x · e
, в) у = ctg 4x · e  , г) y = sin
, г) y = sin  .
. , б) у =
, б) у =  , в) у = cjsx · 3
, в) у = cjsx · 3 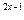 , г) y = ln
, г) y = ln  .
. , б) у =
, б) у =  , в) у = tg 2x ·2
, в) у = tg 2x ·2  , г) y = ln
, г) y = ln  , б) у =
, б) у =  , в) у = arctgx ·(x
, в) у = arctgx ·(x  , г) y = e
, г) y = e  .
. , б) у =
, б) у = 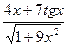 , в) у = cos 3x · e
, в) у = cos 3x · e  б) у =
б) у =  , у = tg2x · 2
, у = tg2x · 2  , г) y = cos ln 5x.
, г) y = cos ln 5x. , б) у =
, б) у =  , в) у = ln2x · e
, в) у = ln2x · e  , г) y = cos
, г) y = cos  .
. , б) у =
, б) у =  , у = sin 4x · e
, у = sin 4x · e  , г) y = arcsin ln 4x.
, г) y = arcsin ln 4x. , б) у =
, б) у =  , в) у = tg 3x · 2
, в) у = tg 3x · 2  , г) y = sin ln 5x.
, г) y = sin ln 5x.