 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Местные сопротивления. Приборы для измерения расхода жидкости.
Министерство образования и науки РФ Федеральное государственное бюджетное образовательное Учреждение высшего образования «Тульский государственный университет» Политехнический институт Кафедра “Механика пластического формоизменения”
СБОРНИК МЕТОДИЧЕСКИХ УКАЗАНИЙ К ПРАКТИЧЕСКИМ ЗАНЯТИЯМ
по дисциплине
ПНЕВМО- И ГИДРОПРИВОДЫ
Направление подготовки (специальность): 15.03.01 Машиностроение Профиль подготовки: Машины и технология обработки металлов давлением Оборудование и технология сварочного производства Машины и технология литейного производства Машины и технология высокоэффективных процессов обработки
Квалификация выпускника: бакалавр.
Форма обучения: очная
Тула 2015
Методические указания к практическим занятиям составлены д.т.н., проф.Черняевым А.В. и к.т.н., доц. Чариным А.В. и обсуждены на заседании кафедры «Механика пластического формоизменения» Политехнического института, протокол № _____ от _____________ 20____ г.
Зав. кафедрой _________________ С.С. Яковлев
Методические указания к практическим занятиям пересмотрены и обсуждены на заседании кафедры «Механики пластического формоизменения» Политехнического института, протокол № _____ от _____________ 20____ г.
Зав. кафедрой _________________ С.С. Яковлев
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №1 Давление жидкости на плоские и криволинейные поверхности Цель занятия Изучение методики определения силы давления жидкости на плоские и криволинейные поверхности произвольной формы. Постановка задачи Щит, перекрывающий канал, расположен под углом Весом щита и трением в шарнире можно пренебречь. Исходные данные для расчета принять по указанию преподавателя.
Рисунок 1.
Теоретические сведения
Сила суммарного давления жидкости
или
где Направление полной силы давления нормально к плоскости стенки. Точка приложения полной силы давления жидкости на стенку называется центром давления. Центр давления вследствие возрастания давления по мере увеличения глубины всегда лежит ниже центра тяжести стенки. Так, например, для прямоугольной стенки центр давления находится на одной трети, а центр тяжести - на половине ее высоты от нижнего основания стенки.
Рисунок 1.1.
Ордината центра давления определяется уравнением
где
Сила суммарного давления жидкости
Горизонтальная составляющая силы суммарного давления жидкости на цилиндрическую стенку равна силе суммарного давления жидкости на вертикальную проекцию
Вертикальная составляющая равна весу жидкости в объеме тела давления:
Телом давления называется объем жидкости, ограниченный сверху уровнем свободной поверхности жидкости, снизу - рассматриваемой криволинейной поверхностью стенки, смоченной жидкостью, и с боков - вертикальным поверхностями, проведенными через границы стенки. Если тело давления образовано жидкостью, то вертикальная составляющая Направление силы суммарного давления
С вопросом определения силы давления жидкости на плоские стенки и цилиндрические поверхности приходится часто сталкиваться при расчетах на прочность различных резервуаров, труб и других гидротехнических сооружений.
Контрольные вопросы 1. Как определяется сила давления жидкости на плоскую стенку? 2. Как определяется сила давления жидкости на цилиндрическую поверхность? 3. Как направлена сила давления жидкости на плоскую и цилиндрическую поверхности? 4. Что называется центром давления и как определяется его положение? 5. Что называется телом давления?
Задания к работам №1-4
Варианты веществ и их плотности :
В работе принять :
Варианты заданий :
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №2 Истечение жидкости через отверстия и насадки Цель занятия Изучение процесса установившегося истечения жидкости из резервуара через круглое отверстие, размер которого мал по сравнению с его заглублением под уровнем жидкости. Постановка задачи Произвести расчет процесса истечения жидкости (рисунок 2) плотностью Определить для установившегося режима системы расход Исходные данные для расчета принять по указанию преподавателя.
Рисунок 2.
Теоретические сведения На практике часто приходится встречаться с истечением жидкости через различные отверстия, при этом характер истечения существенно зависит от условий истечения. Истечение может происходить через малое отверстие, высота или диаметр которого невелики по сравнению с напором. Во всех точках такого отверстия давление практически одинаково (d £ 0,1 Н). Большим отверстием называется такое отверстие, размеры которого в вертикальном направлении значительны по сравнению с напором Н над центром отверстия (d > 0,1 Н). Если линейный размер отверстия d значительно больше толщины стенки d или днища резервуара, в котором оно сделано (d < 3d), то такое отверстие называют отверстием в тонкой стенке. При этом считается, что края отверстия имеют острую кромку. При d ³ 3d отверстие называют отверстием в толстой стенке. Насадком называется короткий патрубок, присоединенный к отверстию в тонкой стенке. Длина насадка обычно составляет Расход Q при истечении через отверстия и насадки определяется по формуле
где w - площадь сечения выходного отверстия или насадка; m - коэффициент расхода, величина которого зависит от вида или насадка. Исходным для решения задачи является условие равенства расходов через боковое и донное отверстия при установившемся режиме (т.е., при постоянных уровнях жидкости). Для выбора расчетных зависимостей необходимо предварительно выяснить условия истечения жидкости через боковое отверстие. Для этого предположим, что
где Расход через донное отверстие
где Если получится, что В первом случае условие равенства расходов дает систему уравнений
Во втором случае
Контрольные вопросы 1. Что понимается под терминами большое и малое отверстие? 2. Поясните понятия отверстия в тонкой и толстой стенке. 3. В чем особенность истечения жидкости через насадок? 4. Какие виды насадков вы знаете, и с какой целью они применяются? 5. От каких факторов зависит величина расхода при истечении жидкости? Варианты заданий :
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №3 Местные сопротивления. Приборы для измерения расхода жидкости. Цель занятия Изучение процесса течения жидкости по трубопроводу с местными сопротивлениями. Теоретические сведения При движении жидкости в трубопроводе часть энергии потока (гидродинамического напора) расходуется на преодоление гидравлических сопротивлений. Последние бывают двух видов : 1) сопротивления трения по длине 2) местные сопротивления К местным сопротивлениям относят внезапное расширение, сужение потока, вентиль, кран и т.д. Величина общих потерь энергии (напора) учитывается дополнительным членом Определение величины потерь энергии (напора) при движении жидкости является одной из основных задач гидродинамики . При движении жидкости в прямой трубе потери энергии определяются формулой Дарси-Вейсбаха
где Местными сопротивлениями называют короткие участки трубопроводов, на которых происходят изменения величины или направления скоростей потока из-за изменения конфигурации твердых границ. Потери энергии в местных сопротивлениях, отнесенные к единице веса потока жидкости, называются местными потерями напора и подсчитываются по общей формуле
где
Величина Величина коэффициента сопротивления входа в трубу из большого резервуара зависит от формы входной кромки. В лабораторной работе При выходе потока из трубы в резервуар потеря напора и коэффициент сопротивления выхода равны:
где
При последовательном расположении в трубопроводе различных местных сопротивлений общая потеря напора определяется как сумма потерь в отдельных сопротивлениях, если между этими местными сопротивлениями имеются участки трубопровода длиной не менее пяти-шести диаметров. На этих участках поток, вышедший из одного местного сопротивления, стабилизируется до входа в следующее сопротивление. При более близком расположении местных сопротивлений необходимо учитывать их взаимное влияние. Далее предполагается, что местные сопротивления достаточно удалены друг от друга и их взаимное влияние отсутствует. Для расходомеров, основанных на создании перепада давлений в потоке различными сужающими устройствами (труба Вентури, сопло и диафрагма - см. рисунок 2), расход определяется по общей формуле
в которой
Величина Потери напора в расходомерах вычисляются по общему выражению (1), где
где
Постановка задачи
Пусть жидкость плотностью
Рисунок 3. На трубопроводе установлены расходомер Вентури с диаметром узкого сечения Требуется определить расход Исходные данные для расчета принять по указанию преподавателя. Расход в трубопроводе по показанию дифференциального манометра на трубе Вентури равен согласно формуле (2)
где перепад пьезометрических уровней равен:
Для определения давления
где Так как скоростные напоры в баках пренебрежимо малы (
выражающее, что разность В данном случае
Пренебрегая потерями трения по длине трубопровода (который предполагается коротким), определим местные потери: при входе в трубопровод
Таким образом, искомое давление
Контрольные вопросы 1. Что понимается под гидравлическими потерями? 2. Какие существуют виды гидравлических потерь? 3. Что такое местные сопротивления? Приведите примеры. 4. От чего зависит величина местных потерь? 5. В чем заключается принцип действия расходомера Вентури?
В работах №3-4 принять :
Варианты заданий :
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №4 Расчет трубопроводов. Цель занятия Произвести расчет трубопровода с учетом потерь на трение по длине и потерь в местных сопротивлениях, расположенных на трубопроводе. Теоретические сведения Трубопровод, диаметр которого постоянен по всей длине и который не имеет боковых ответвлений, называется простым трубопроводом. На простом трубопроводе обычно имеется некоторое количество фасонных частей, создающих местные сопротивления. По простому трубопроводу жидкость транспортируется от питателя к одному приемнику. Питателями и приемниками в гидросистемах могут являться различные устройства - насосы и гидродвигатели, аккумуляторы, резервуары и др. Трубопровод может иметь постоянный диаметр по всей длине, или же может состоять из ряда последовательно соединенных участков различного диаметра. Трубопровод, имеющий разветвления, а также составленный из труб разных диаметров, называется сложным трубопроводом. Различают короткие трубопроводы, в которых потери напора на местные сопротивления велики и соизмеримы с потерями напора по длине (всасывающие трубы центробежных насосов и т.д.), и длинные трубопроводы, в которых потери напора на местные сопротивления составляют незначительную часть от потерь по длине (не более 5-10%). Исходным при расчетах простого трубопровода является уравнение баланса напоров (уравнение Бернулли) для потока от сечения
где Для удобства расчетов вводится понятие располагаемого напора трубопровода
который представляет перепад гидростатических напоров в питателе и приемнике и выражается разностью пьезометрических уровней в сечениях Преобразуя уравнение баланса напоров, получаем общий вид расчетного уравнения простого трубопровода
Если площади сечений питателя и приемника достаточно велики по сравнению с сечением трубопровода (например, трубопровод, соединяющий два больших резервуара), скоростными напорами жидкости в этих сечениях можно при составлении баланса напоров пренебречь. При этом расчетное уравнение приобретает вид
отвечая процессу, в котором весь располагаемый напор затрачивается на преодоление гидравлических сопротивлений. Уравнение (2) применимо также независимо от размеров питателя и приемника в тех случаях, когда трубопровод имеет достаточно большую длину, при которой скоростные напоры на входе и выходе из трубопровода оказываются пренебрежимо малыми по сравнению с потерями напора на трение по его длине. Применим уравнение (2) к горизонтально расположенному трубопроводу, который соединяет два больших резервуара с постоянными уровнями жидкости и состоит из Выражая потери на трение по длине и местные потери напора общими формулами
получим
где Расчет трубопровода на основе приведенных выше соотношений связан с выбором коэффициентов сопротивления трения 1. Ламинарный режим (
где 2. Турбулентный режим ( а) Для гидравлически гладких труб коэффициент сопротивления трения может определяться по формуле Конакова
б) Для гидравлически шероховатых труб коэффициент сопротивления трения может определяться формулой Шифринсона (
где Постановка задачи Произвести расчет трубопровода, представленного на рисунке 4. Длины и диаметры сегментов трубопровода заданы. Определить располагаемый напор Исходные данные для расчета принять по указанию преподавателя.
Рисунок 4.
Контрольные вопросы 1. Какие трубопроводы называются простыми, а какие сложными? 2. Что понимается под терминами длинный и короткий трубопроводы? 3. От чего зависит величина потерь по длине трубопровода? 4. Приведите уравнение Бернулли. 5. В каких случаях трубы считаются гидравлически гладкими и гидравлически шероховатыми? 6. Как определяется режим движения жидкости?
В работе принять тип труб ( ТТр ) :
Варианты заданий : <
©2015 www.megapredmet.ru Все права принадлежат авторам размещенных материалов. |



 к горизонту и закреплен шарнирно к опоре над жидкостью (рисунок 1). Определить усилие, которое необходимо приложить к тросу для открывания щита, если заданы ширина щита
к горизонту и закреплен шарнирно к опоре над жидкостью (рисунок 1). Определить усилие, которое необходимо приложить к тросу для открывания щита, если заданы ширина щита  , глубина жидкости перед щитом
, глубина жидкости перед щитом 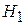 , и после щита
, и после щита  . Шарнир расположен над высоким уровнем жидкости на расстоянии
. Шарнир расположен над высоким уровнем жидкости на расстоянии  .
.
 на плоскую стенку равна произведению смоченной площади стенки
на плоскую стенку равна произведению смоченной площади стенки  и гидростатического давления в центре тяжести этой площади
и гидростатического давления в центре тяжести этой площади  , т. е. (рисунок 1.1);
, т. е. (рисунок 1.1);
 ,
, - глубина погружения центра тяжести смоченной площади стенки.
- глубина погружения центра тяжести смоченной площади стенки.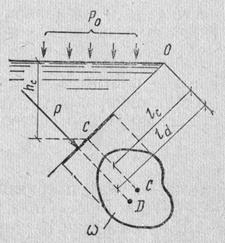
 ,
, - момент инерции смоченной площади стенки относительно горизонтальной оси, проходящей через центр тяжести этой площади;
- момент инерции смоченной площади стенки относительно горизонтальной оси, проходящей через центр тяжести этой площади;  и
и  - соответственно расстояния центра тяжести стенки и центра давления от линии пересечения плоскости стенки со свободной поверхностью.
- соответственно расстояния центра тяжести стенки и центра давления от линии пересечения плоскости стенки со свободной поверхностью. и вертикальной
и вертикальной  , т.е.
, т.е. .
. этой стенки:
этой стенки: .
.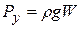
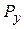 направлена вниз. Если тело давления образовано воздухом, то
направлена вниз. Если тело давления образовано воздухом, то  , образуемым вектором
, образуемым вектором  .
. , кг/м3
, кг/м3 , м2/с
, м2/с

 (расположенное в боковой стенке на высоте
(расположенное в боковой стенке на высоте  ) и вытекающей затем в атмосферу через донное отверстие диаметром
) и вытекающей затем в атмосферу через донное отверстие диаметром 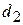 .
. из бака и высоту
из бака и высоту  уровня в правой секции, считая известными высоту уровня
уровня в правой секции, считая известными высоту уровня  и показание манометра
и показание манометра  в левой секции.
в левой секции.
 , где d -диаметр выходного отверстия в стенке. Характер истечения через насадок отвечает условиям истечения жидкости через отверстие в толстой стенке. При этом протекающая струя испытывает сопротивление по длине. Насадки применяются главным образом для увеличения пропускной способности отверстия.
, где d -диаметр выходного отверстия в стенке. Характер истечения через насадок отвечает условиям истечения жидкости через отверстие в толстой стенке. При этом протекающая струя испытывает сопротивление по длине. Насадки применяются главным образом для увеличения пропускной способности отверстия. ,
, , тогда расход через боковое отверстие
, тогда расход через боковое отверстие
 - высота пьезометрического уровня в левой секции,
- высота пьезометрического уровня в левой секции,  - коэффициент расхода для бокового отверстия.
- коэффициент расхода для бокового отверстия.
 - коэффициент расхода для донного отверстия.
- коэффициент расхода для донного отверстия. , то в действительности
, то в действительности  и боковое отверстие затоплено; если
и боковое отверстие затоплено; если  , то
, то 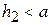 и боковое отверстие не затоплено.
и боковое отверстие не затоплено.





 , пропорциональные длине потока;
, пропорциональные длине потока; , возникновение которых связано с изменением направления или скорости в том или ином сечении потока .
, возникновение которых связано с изменением направления или скорости в том или ином сечении потока . в уравнении Бернулли для реальной жидкости.
в уравнении Бернулли для реальной жидкости. ,
, (1)
(1) - средняя скорость потока;
- средняя скорость потока; - безразмерный коэффициент местного сопротивления.
- безразмерный коэффициент местного сопротивления. принять равным 0,5.
принять равным 0,5.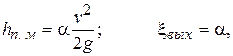
 - коэффициент кинетической энергии. В лабораторной работе положить
- коэффициент кинетической энергии. В лабораторной работе положить  .
. (2)
(2) - падение гидростатического напора (пьезометрического уровня) на участке между входным и суженным сечениями потока в расходомере;
- падение гидростатического напора (пьезометрического уровня) на участке между входным и суженным сечениями потока в расходомере;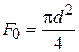 - наименьшая проходная площадь расходомера;
- наименьшая проходная площадь расходомера;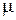 - коэффициент расхода.
- коэффициент расхода. и
и 
 и
и  площади трубы и отверстия расходомера соответственно;
площади трубы и отверстия расходомера соответственно;  - коэффициент сопротивления отверстия диафрагмы;
- коэффициент сопротивления отверстия диафрагмы; 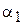 и
и  - значения коэффициента кинетической энергии в сечении перед входом в расходомер и в сжатом сечении струи (при расчетах принять
- значения коэффициента кинетической энергии в сечении перед входом в расходомер и в сжатом сечении струи (при расчетах принять  - коэффициент потерь в диффузоре.
- коэффициент потерь в диффузоре. перетекает по трубопроводу диаметром
перетекает по трубопроводу диаметром  из бака
из бака  в бак
в бак  с постоянной разностью уровней
с постоянной разностью уровней  под избыточным давлением
под избыточным давлением  в баке
в баке 
 и задвижка. Коэффициенты сопротивления задвижки
и задвижка. Коэффициенты сопротивления задвижки 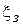 и сходящегося участка расходомера
и сходящегося участка расходомера  в трубопроводе, давление
в трубопроводе, давление 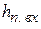 ; в расходомере Вентури
; в расходомере Вентури  ; на задвижке
; на задвижке 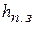 ; при выходе из трубопровода
; при выходе из трубопровода  , считая известным показание
, считая известным показание 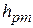 ртутного дифференциального манометра, присоединенного к трубе Вентури.
ртутного дифференциального манометра, присоединенного к трубе Вентури.

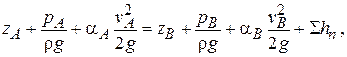
 - сумма потерь напора между этими сечениями.
- сумма потерь напора между этими сечениями. и
и  ), получаем общее соотношение
), получаем общее соотношение
 гидростатических напоров (пьезометрических уровней) в баках целиком затрачивается на преодоление гидравлических сопротивлений, возникающих при перетекании жидкости по трубопроводу.
гидростатических напоров (пьезометрических уровней) в баках целиком затрачивается на преодоление гидравлических сопротивлений, возникающих при перетекании жидкости по трубопроводу. и избыточное давление
и избыточное давление  ; следовательно:
; следовательно:
 ; в расходомере Вентури
; в расходомере Вентури  ; на задвижке
; на задвижке  ; при выходе из трубопровода
; при выходе из трубопровода  , где средняя скорость в трубопроводе
, где средняя скорость в трубопроводе











 в питателе перед входом в трубопровод до сечения
в питателе перед входом в трубопровод до сечения  в приемнике после выхода жидкости из трубопровода. При установившемся движении жидкости имеем
в приемнике после выхода жидкости из трубопровода. При установившемся движении жидкости имеем

 и
и  (1)
(1) (2)
(2) последовательных участков длиной
последовательных участков длиной  и диаметром
и диаметром  .
.

 - средняя скорость потока в каждом участке (определяется из уравнения расхода
- средняя скорость потока в каждом участке (определяется из уравнения расхода 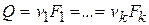 );
);  и
и 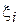 - коэффициент сопротивления трения и суммарный коэффициент местных сопротивлений на каждом участке;
- коэффициент сопротивления трения и суммарный коэффициент местных сопротивлений на каждом участке;  - средняя скорость потока в выходном сечении трубопровода;
- средняя скорость потока в выходном сечении трубопровода;  - потря напора при выходе из трубопровода в резервуар.
- потря напора при выходе из трубопровода в резервуар. , которые при различных режимах движения жидкости определяются следующими зависимостями:
, которые при различных режимах движения жидкости определяются следующими зависимостями: ). Коэффициент сопротивления трения
). Коэффициент сопротивления трения  определяется по выражению
определяется по выражению
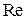 - число Рейнольдса
- число Рейнольдса  .
. ).
).
 в [мм],
в [мм],  в [м])
в [м])
 .
.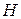 .
.



