 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Енергія гармонічних коливань
Розв’язок диференційного рівняння незатухаючих гармонічних коливань
Розв’яжемо рівняння (1.16) для електричних коливань, яке являється лінійним однорідним диференційним рівнянням другого порядку з постійними коефіцієнтами. Порядок його розв’язку був розглянутий у розділі 1.2. Складаємо характеристичне алгебраїчне рівняння
Константи інтегрування А і В знайдемо із початкових умов: при t = 0 Знайдемо закон зміни струму з часом, продиференціювавши рівняння (1.17). Підставляємо умови (1.18) в (1.17) і (1.19). Маємо систему алгебраїчних рівнянь
Аналогічно для механічних коливань зміщення від положення рівноваги
Рівняння (1.20), (1.21) називаються рівняннями гармонічних незатухаючих коливань. Намалюємо графіки цих коливань.
Характеристики гармонічних коливань. Фазові співвідношення
В загальному випадку (при інших початкових умовах, ніж (1.18) рівняння гармонічних коливань мають вид
Зміщенняx(t), q(t) – відхилення фізичної величини від рівноважного значення в момент часу t. Амплітудахо, qo – найбільше відхилення фізичної величини від рівноважного значення. Фактично це коефіцієнт перед гармонічною функцією. Для незатухаючих коливань амплітуда постійна, при затухаючих вона зменшується з часом. Фаза Початкова фаза φ – будучи поділеною на 2π показує кількість коливань, що відбулися до моменту початку відліку часу. Період Т – Час одного повного коливання. За період фаза коливань змінюється на 2π, тобто маємо
В розділі 1.3 були введені позначення дає вирази для періодів коливань: пружинного маятника у коливальному контурі (формула Томсона) Частотаν – кількість коливань за одиницю часу Вимірюється частота в Герцах 1Гц = 1 с-1. Циклічна частотаωо - кількість коливань за 2π секунд.
Знайдемо закон зміни з часом струму І(t) і напруг на конденсаторі Uc(t) і на котушці UL(t) коливального контуру, виходячи з закону зміни заряду (1.20). Скористаємось також формулами додаткового кута, щоб всі закони виразити через одну гармонічну функцію, наприклад, сos.
Одержали, що фази струму і напруг не співпадають. Напруга на конденсаторі відстає по фазі від струму на  , а на котушці випереджає на , а на котушці випереджає на  . Фази напруг на конденсаторі і на котушці відрізняються на . Фази напруг на конденсаторі і на котушці відрізняються на  , що складає половину періоду гармонічної функції. Тому кажуть, що напруги на конденсаторі і на котушці змінюються в протифазі. Намалюємо графіки зміни струму і напруг. , що складає половину періоду гармонічної функції. Тому кажуть, що напруги на конденсаторі і на котушці змінюються в протифазі. Намалюємо графіки зміни струму і напруг. У виразах (1.28) – (1.30) були позначені амплітуди напруг і струму:
Згідно із законом Ома для дільниці кола, відношення напруги до струму дорівнює опорові. Це дає можливість знайти реактивні опори конденсатора ХС і котушки ХL:
Енергія гармонічних коливань
Отже повна механічна енергія пружинного маятника при незатухаючих коливаннях не залежить від часу, тобто залишається сталою. Відбувається перетворення потенціальної енергії к кінетичну і навпаки. Вона, як видно із (1.36) пропорційна квадрату амплітуди і квадрату частити і дорівнює максимальній кінетичній, або максимальній потенціальній енергії. Енергія незатухаючих коливань у коливальному контурі
також не залежить від часу, пропорційна квадрату амплітуди і квадрату частоти і дорівнює максимальній енергії електричного поля конденсатора, або максимальній енергії магнітного поля котушки. Хвилі |



 . Його корені
. Його корені  . Загальний розв’язок рівняння (1.16) записуємо у вигляді (1.11)
. Загальний розв’язок рівняння (1.16) записуємо у вигляді (1.11) . (1.17)
. (1.17) . (1.18)
. (1.18) . (1.19)
. (1.19) . Отже із (1.17) одержуємо
. Отже із (1.17) одержуємо  (1.20) гармонічний закон зміни заряду. Тут врахована формула Ейлера
(1.20) гармонічний закон зміни заряду. Тут врахована формула Ейлера , яку можна одержати, скориставшись степеневими рядами (1.5)-(1.8).
, яку можна одержати, скориставшись степеневими рядами (1.5)-(1.8). . (1.21)
. (1.21)
 (1.22)
(1.22) –аргумент гармонічної функції. Якщо фазу поділити на період гармонічної функції 2π, одержимо кількість коливань, які відбулися від початку коливань до моменту часу t.
–аргумент гармонічної функції. Якщо фазу поділити на період гармонічної функції 2π, одержимо кількість коливань, які відбулися від початку коливань до моменту часу t. , або
, або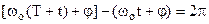 . Після спрощень одержуємо
. Після спрощень одержуємо . (1.23)
. (1.23) для пружинного маятника і
для пружинного маятника і  для коливального контура. Підстановка в (1.23)
для коливального контура. Підстановка в (1.23) ; (1.24)
; (1.24) . (1.25)
. (1.25) . (1.26)
. (1.26) . (1.27)
. (1.27) ; (1.28)
; (1.28) ; (1.29)
; (1.29) . (1.30)
. (1.30)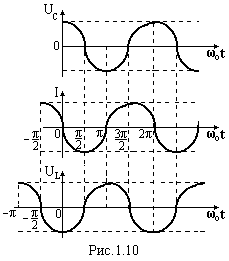
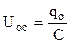 , (1.31)
, (1.31)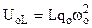 , (1.32)
, (1.32) . (1.33)
. (1.33) ; (1.34)
; (1.34)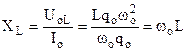 . (1.35)
. (1.35) . Врахуємо, що
. Врахуємо, що  ,
,  (див. розділ 1.3), одержуємо
(див. розділ 1.3), одержуємо 

 . Враховуючи (1.20), (1.29) і маємо
. Враховуючи (1.20), (1.29) і маємо  . Так як
. Так як  , одержуємо
, одержуємо 
 (1.36)
(1.36)