 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Электропроводность растворов
МЕТОДИЧЕСКИЕ УКАЗАНИЯ для выполнения контрольной работы по дисциплине
Б2.В.4 Физическая и коллоидная химия Направление подготовки бакалавра
Технология продукции и организация общественного питания (заочное отделение)
Уфа - 2014
УДК 541.1/.18(07)
Рекомендовано к изданию методической комиссией факультета пищевых технологий (протокол № 5 от 24 февраля 2014 г.)
\
Составители: доцент Нигматуллин Н.Г., доцент Ганиева Е.С.
Рецензент: доцент кафедры кормления животных и физиологии Н.Л.Нурмухаметова
Ответственный за выпуск: заведующая кафедрой химии Ярмухамедова Э.И.
ВВЕДЕНИЕ
Физическая и коллоидная химия имеют большое практическое значение. Они открывают широкие возможности активного управления химико-технологическими процессами, рационального использования сырья, повышения качества продукции, экономии энергетических ресурсов, защиты окружающей среды и т.д. Данное методическое пособие является практическим руководством для выполнение контрольной работы по дисциплине «Физическая и коллоидная химия», в котором представлены задания по основным разделам физической и коллоидной химии: химическая термодинамика, фазовые равновесия, химическая кинетика и электрохимия, адсорбция, коллоидные системы, устойчивость коллоидных систем, микрогетерогенные системы. Каждый студент выполняет задания согласно варианту, определяемому по последним двум цифрам номера зачетной книжки (таблица 1). Следует обратить внимание на то, что некоторые задачи имеют общие условия, а данные представлены в обобщенных таблицах. Для каждой из этих задач исходные данные для расчета нужно брать в таблице напротив номера задачи, соответствующего вашему варианту.
Таблица 1. Варианты и задания к ним
ХИМИЧЕСКАЯ ТЕРМОДИНАМИКА Химическая термодинамика является наукой об энергетических эффектах химических реакций, их направлении и равновесии. Изучает применение законов термодинамики к химическим и физико-химическим процессам. Термодинамический метод полезен тем, что позволяет: - установить взаимосвязь между параметрами равновесной системы, что дает возможность вычислить неизвестный параметр системы по другим известным параметрам; - оценить величину изменения параметров системы при осуществлении какого-либо процесса в ней; - определить параметры системы после перехода ее их одного состояния в другое термодинамическое состояние или из одного технологического режима в другой режим проведения процесса; - определить принципиальную возможность протекания процесса в нужном направлении; - оценить глубину протекания процесса в зависимости от условий. До выполнения задания по химической термодинамике следует проработать лекционный материал соответствующего раздела. По учебнику [1] изучить теоретический материал и разобрать решения типовых задач по задачнику [2]. При определении параметров простейших термодинамических процессов идеальных газов советуем воспользоваться формулами, приведенными в таблицах 1.1 и 1.2. Необходимо обратить особое внимание на правильное применение соответствующих размерностей параметров. Используйте следующие значения универсальной газовой постоянной: R = 8,31 Дж/(моль·К) = 1,98 кал/(моль·К) = 0,082(л·атм)/(моль·К). Тепловой эффект реакций при стандартных условиях определяется по формуле
Соответствующие значения При расчете тепловых эффектов при других температурах необходимо опираться на закон Кирхгофа и на вытекающее из него уравнение
в котором
где индекс i – стехиометрические коэффициенты соответствующих исходных реагентов; j – стехиометрические коэффициенты соответствующих продуктов реакции. При этом можно сделать следующие допущения: 1. 2.
3.
из которой следует
где Изменение энтропии реакции при стандартных условиях определяются исходя из значений S0 (таблица 1.4) по формуле:
При определении
Вычисление
Значение
По знаку величин Если: DG < 0 – самопроизвольное протекание химической реакции возможно; DG > 0 – самопроизвольное протекание химической реакции невозможно; DG = 0 – система находится в равновесии.
Литература:[1], с.59 – 105; [2], с.23 – 25, 32 – 34, 43 – 46, 57 – 59.
Таблица 1.1 Связь между основными параметрами состояния в изопроцессах и определение их функции перехода для n молей вещества (
Таблица 1.2 Изменение функций состояния системы в изопроцессах (n - количество вещества,
Примеры решения задач
Пример 1.1Рассчитайте изменение внутренней энергии гелия (одноатомный идеальный газ) при изобарном расширении от 5 до 10 л под давлением 196 кПа. Решение: Из таблицы 1.2 для изобарного процесса находим ΔU=ncv(T2 – T1), т.е. изменение внутренней энергии идеального газа определяется только начальной и конечной температурой: T1 = p1V1 /nR, T2 = p2V2 /nR. Для одноатомного идеального газа cv = DU = ncv (T2 – T1) = Ответ: DU = 1470 Дж. Пример 1.2 Рассчитайте энтальпию сгорания метана при 1000 К, если даны энтальпии образования при 298 К: DH°обр (CH4) = -17,9 ккал/моль, DH°обр (CO2) = -94,1 ккал/моль, DH°обр (H2O(г)) = -57,8 ккал/моль. Теплоемкости газов в интервале от 298 до 1000К равны: сp (CH4) = 3,422 + 0,0178 × T; сp (O2) = 6,095+ 0,0033 × T; сp (CO2) = 6,396 + 0,0102 × T; сp (H2O(г)) = 7,188 + 0,0024 × T. Решение: Запишем уравнение процесса: CH4 (г) + 2O2 (г) ® CO2 (г) + 2H2O (г) Энтальпия реакции при температуре Т рассчитывается по закону Кирхгоффа Чтобы им воспользоваться, необходимо рассчитать стандартную энтальпию реакции DH0298и Dc - разность суммы теплоемкостей продуктов и исходных реагентов
где индекс i – стехиометрические коэффициенты соответствующих исходных реагентов; j – стехиометрические коэффициенты соответствующих продуктов реакции. Стандартный тепловой эффект реакции определяется по формуле
Для данной химической реакции: DH°298 = DH°обр (CO2) + 2 ∙ DH°обр (H2O) – DH°обр (CH4) = -94,1 + 2 × (-57,8) – (-17,9) = = -191,8 ккал. Dс = с (CO2) + 2 ∙ с (H2O) – с (CH4) - 2 ∙ с (O2) = 6,396 + 0,0102 × Т + 2 × (7,188 + +0,0024 × Т) – 3,422 – 0,0178 × Т – 2 × (6,095 + 0,0033 × Т) = 5,16 – 0,0094 ×Т.
Контрольные задания 1.Термодинамическая система. Классификация систем. 2.Параметры термодинамической системы. 3.Термодинамические процессы. 4.Нулевое начало термодинамики. Понятие температура. 5.Понятие о внутренней энергии, теплоте и работе. Математическое выражение первого закона термодинамики. 6.Первый закон термодинамики для изохорного и изобарного процессов. Понятие об энтальпии. 7.Тепловой эффект химической реакции, теплота образования химического вещества, теплота сгорания химического вещества. 8.Термохимия. Закон Гесса и следствия из него. 9.Удельная, молярная, средняя и истинная теплоемкость. Уравнение для теплоемкости. 10.Зависимость теплового эффекта от температуры. Уравнение Кирхгофа. 11. Энтропия и термодинамическая вероятность. Расчет изменения энтропии для различных процессов. 12.Третье начало термодинамики. Расчет абсолютного значения энтропии. 13.Второе начало термодинамики. 14.Термодинамические потенциалы. Использование свободной энергии Гиббса и свободной энергии Гельмгольца для оценки возможности самопроизвольного протекания процессов. 15.Газ, расширяясь от 10 л до 16 л при постоянном давлении 101,3 кПа, поглощает 126 Дж теплоты. Определите изменение внутренней энергии газа. 16.Определите изменение внутренней энергии, количество теплоты и работу, совершаемую при обратимом изотермическом расширении азота от 0,5 до 4 м3 (начальные условия: температура 26,8 °С, давление 93,2 кПа). 17.Один моль идеального газа, взятого при 25 °С и 100 атм, расширяется обратимо и изотермически до 5 атм. Рассчитайте работу, поглощенную теплоту, изменение внутренней энергии и энтальпии. 18.Какое количество теплоты необходимо для повышения температуры 16 г кислорода от 300 до 500 К при давлении 1 атм? Как при этом изменится внутренняя энергия? 19.Чайник, содержащий 1 кг кипящей воды, нагревают до полного испарения при нормальном давлении. Определите работу, количество теплоты, изменение внутренней энергии и энтальпии для этого процесса. Мольная теплота испарения воды 40,6 кДж/моль. 20.Определите конечную температуру и работу, необходимую для адиабатического сжатия азота от 10л до 1 л, если начальные температура и давление равны 26,8°С и 101,3 кПа соответственно. 21.Рассчитайте количество теплоты, необходимое для нагревания воздуха в квартире общим объемом 600 м3 от 20 до 25 °С. Примите, что воздух – идеальный двухатомный газ, а давление при исходной температуре нормальное. Найдите изменение внутренней энергии и энтальпии для процесса нагревания воздуха. 22.Вычислите стандартную энтальпию реакции S (т) + O2 (г) → SO2 (г) , используя данные: 2S (т) + 3O2 (г) → 2SO3 (г), DH° = - 790 кДж, 2SO2 (г) + O2 (г) → SO3 (г), DH° = - 196 кДж. 23. Вычислите тепловой эффект перехода C (алмаз) → C (графит), используя данные: C (графит) + O2 (г) → CO2 (г), DH° = - 396,3 кДж, C (алмаз) + O2 (г) → CO2 (г), DH° = - 398,2 кДж. 24.Вычислите тепловой эффект перехода S (моноклинная) → S (ромбическая), используя данные: S (моноклинная) + O2 (г) → SO2 (г), DH° = - 296,96 кДж, S (ромбическая) + O2 (г) → SO2 (г), DH° = - 396,65 кДж. 25. Определите стандартную энтальпию образования этилена C2H4 по следующим данным: C2H4 (г) +3O2 (г) → 2CO2 (г) + 2H2O (г), DH° = - 1323 кДж C (графит) + O2 (г) → CO2 (г), DH° = - 393,5 кДж, H2 (г) + 1/2O2 (г) → H2O (г), DH° = - 241,8 кДж. 26. Вычислите тепловой эффект реакции CH3OCH3 (г) → CH3CH2OH (г), если CH3OCH3 (г) + 3O2 (г) → 2CO2 (г) + 3H2O (г), DH° = - 1454 кДж, CH3CH2OH (г) + 3O2 (г) → 2CO2 (г) + 3H2O (г), DH° = - 1402 кДж. 27. Вычислите тепловой эффект реакции Na2CO3 (к) → Na2O (к) + CO2 (г), если известно Na2CO3 (к) + SiO2 (к)→ Na2SiO3 (к) + CO2 (г), DH° = 81,04 кДж, Na2O (к) + SiO2 (к)→ Na2SiO3 (к), DH° = - 243,17 кДж. 28. Рассчитайте мольную энтропию неона при 500К, если при 298 К и том же объеме энтропия неона равна 146,2 Дж/моль ×К. 29.Рассчитайте изменение энтропии при нагревании 11,2 л азота от 0 °С до 50 °С и одновременном уменьшении давления от 1 атм до 0,01 атм. 30.Один моль гелия при 100° С и 1 атм смешивают с 0,5 моль неона при 0° С и 1 атм. Определите изменение энтропии, если конечное давление равно 1 атм. 31. Три моля идеального одноатомного газа (Cv = 3 кал /моль ×К), находящегося при 350 К и давлении 5 атм, обратимо и адиабатически расширяются до давления 1 атм. Рассчитайте конечные температуру, объем, совершенную работу, изменение внутренней энергии, энтальпии и энтропии в этом процессе. 32. Рассчитайте изменение энтропии при нагревании 0,4 моль NaCl от 20° до 850° С. Мольная теплоемкость равна: Cp (NaClтв) = 45,94 + 16,32×10-3×T Дж/моль×К, Cp (NaClж) = 66,53 Дж/моль× К. Температура плавления хлорида натрия 800 °С, теплота плавления 31 кДж/моль. 33. Рассчитайте изменение энтропии при смешении 5 кг воды при 80 °С с 10 кг воды при 20 °С. Удельную теплоемкость воды принять равной 4,184 Дж/г× К. 34.Рассчитайте изменение энтропии при добавлении 200 г льда, находящегося при температуре 0 °С, к 200 г воды (90 °С) в изолированном сосуде. Теплота плавления льда равна 6 кДж/моль. Удельную теплоемкость воды принять равной 4,184 Дж/г× К.
35 – 52. Для реакции, приведенной в таблице 1.3: 1) рассчитайте стандартный тепловой эффект реакции по известным величинам стандартных теплот образования исходных веществ и продуктов реакции; 2) определите DНт из предположения: а) Dс = 0; б) Dс = const; в) Dс = f (Т). 3) определите 4) вычислите значение Термодинамические характеристики веществ приведены в таблице 1.4
Таблица 1.3 Уравнения реакций для различных вариантов
Таблица 1.4 Термодинамические характеристики веществ
ФАЗОВЫЕ РАВНОВЕСИЯ Термодинамическая теория фазовых равновесий и растворов позволяет на основе опытных данных по диаграммам состояния теоретически предвидеть и рассчитать условия для получения нужных продуктов путем испарения, кристаллизации, экстракции и других фазовых переходов. Прежде чем приступить к решению задач по разделу фазовые равновесия, следует проработать соответствующий лекционный материал. По учебнику [1] изучить теоретический материал и разобрать решения типовых задач по задачнику [2]. При выполнении задания следует учесть, что общие закономерности, которым подчиняются равновесные системы, содержащие любое число фаз и компонентов, устанавливаются «правилом фаз» Гиббса, согласно которому
где К – число компонентов системы, Ф – число фаз, n – число внешних факторов, определяющих существование системы (p, T, c), С – число степеней свободы, показывающая число переменных, которым можно придавать произвольные значения, не изменяя число фаз. Количественно условие равновесия фаз в однокомпонентных системах выражается уравнением Клаузиуса:
где Интегрирование уравнения Клаузиуса из предположения
Поэтому для системы газ-жидкость тангенс угла наклона зависимости ln р =f( 1/Т) дает значение Температуру кипения Ткип вещества при нормальном давлении определяют по формуле, полученной из уравнения Клаузиуса-Клапейрона:
Для проверки применимости правила Трутона к данной системе необходимо найти отношение Взаимосвязь параметров в равновесной системе газ-твердое тело выражается уравнением:
Теплоту плавления вещества
Параметры процесса возгонки определяют по следующим формулам:
Литература:[1], с. 152 – 181, 210 - 220; [2], с. 67 – 71. Контрольные задания
53. Компонент, фаза, число термодинамических степеней свободы системы. Основной закон фазового равновесия или правило фаз Гиббса. 54. Уравнение Клаузиуса. Применение данного уравнения для описания процессов плавления, испарения, возгонки. 55. Однокомпонентные гетерогенные системы. Диаграмма состояния воды. 56. Однокомпонентные гетерогенные системы. Диаграмма состояния серы как пример энантиотропного превращения. 57. Однокомпонентные гетерогенные системы. Диаграмма состояния бензофенона как пример монотропного превращения. 58. Закон Рауля для смеси летучих жидкостей. Положительные и отрицательные отклонения от закона Рауля. 59. Разделение неограниченно смешивающихся жидкостей с помощью фракционной перегонки. 1-ый закон Коновалова 60. Азеотропные смеси. 2 –ой закон Коновалова. Методы разделения азеотропных смесей. 61. Диаграмма состояния двухкомпонентной системы с ограниченной растворимостью в жидкой фазе. Критическая температура растворимости. Правило Алексеева. Правило рычага. 62. Несмешивающиеся жидкости. Перегонка с водяным паром. 63. Физико – химический анализ. Принцип непрерывности и принцип соответствия. Применение термического анализа для построения диаграмм состояния двухкомпонентной системы. 64. Диаграмма состояния двухкомпонентой системы с эвтектикой. 65. Диаграмма состояния двухкомпонентой системы с химическим соединением, плавящимся конгруэнтно. Правило рычага. 66. Диаграмма состояния двухкомпонентой системы с химическим соединением, плавящимся инконгруэнтно. Правило рычага. 67. Диаграмма состояния двухкомпонентной системы с неограниченной растворимостью компонентов в твердом состоянии. Правило рычага. 68. Диаграмма состояния двухкомпонентной системы с ограниченной растворимостью компонентов в твердом состоянии (1 – ый тип). Правило рычага. 69. Диаграмма состояния двухкомпонентной системы с ограниченной растворимостью компонентов в твердом состоянии (2– ой тип). Правило рычага. 70. Фазовая диаграмма состояния трехкомпонентной системы с неограниченно смешивающимися компонентами. Использование метода Гиббса и Розебума для определения состава системы. 71. Фазовая диаграмма состояния трехкомпонентной системы с ограниченно смешивающимися компонентами. Правило Тарасенкова. 72. Молярная теплота испарения воды равна 43,09 кДж/моль. Давление насыщенного водяного пара при температуре 40 °С равно 55,3 мм рт.ст. Чему равно давление насыщенного пара при температуре 50 °С? 73. Давление паров над жидким галлием при температуре 1029 °С равно 0,01 мм рт.ст. , а при 1154 °С - 0,1 мм рт.ст. Чему равна молярная теплота испарения галлия? 74. Молярная энтальпия плавления льда равна 6,01 кДж/моль, а энтальпия испарения воды 41,09 кДж/моль. Чему равна молярная энтальпия возгонки льда? 75. Давление пара над серной кислотой при температуре 451 К равно 666Па, а при температуре 484,5 К - 2666 Па. Определите теплоту парообразования серной кислоты, считая ее постоянной в указанном интервале температуры. 76. Зависимость давления [Па] насыщенного пара над жидким TiCl4 описывается уравнением ln p = 19,688 – 3335/Т. Рассчитайте энтальпию и энтропию парообразования одного моля тетрахлорида титана при нормальной температуре кипения. 77. Под давлением 0,1013 МПа лед плавится при 273К. Удельный объем льда при 273 К равен 991,1 см3/кг, а воды – 916,6 см3/кг. Молярная теплота плавления льда равна 6010 Дж/моль. Вычислите давление, при котором лед будет плавиться при 271 К. 78. Плотности жидкого и твердого олова при температуре плавления (231,9 °С) равны 6,980 г/см3 и 7,184 г/см3, соответственно. Энтальпия плавления олова равна 1, 690 ккал/моль. Определите температуру олова под давлением 500 атм. Молярная масса олова равна 118,7 г/моль. 79. При замерзании бензола (5,5 °С) его плотность изменяется от 0,879г/см3 до 0, 891 г/см3. Энтальпия плавления равна 10,59 кДж/моль. Определите температуру плавления бензола при давлении 1000 атм. 80. Плотности жидкой и твердой ртути при температуре плавления (-38,87 °С) равны 13,690 и 14,193 г/см3, соответственно. Энтальпия плавления ртути равна 2,33 кал/г. Определите температуру плавления ртути при давлении 3000 атм. 81. Температура кипения жидкого метанола равна 34,7 °С при давлении 200 Торр и 49,9 °С при давлении 400 Торр. Найдите температуру кипения метанола при нормальном давлении. 82. Давление пара диэтилового эфира при 10 °С равно 286,8 Торр, а при 20 °С – 432,8 Торр. Определите мольную энтальпию испарения и нормальную температуру кипения эфира. 83. Давление пара дихлорметана при 24,1 °С равно 400 Торр, а его энтальпия испарения равна 28,7 кДж/моль. Рассчитайте температуру, при которой давление пара будет равно 500 Торр. 84. Давление пара твердого СО2 равно 133 Па при -134,3 °С и 2660 Па при -114,4 °С. Рассчитайте энтальпию возгонки. 85. Давление пара (Торр) жидкости в интервале температур 200 – 260 К описывается уравнением: ln p = 16,225 – 2501,8/T. Рассчитайте энтальпию испарения и нормальную точку кипения жидкости. 86. Давление пара (Торр) жидкого бензола в интервале температур 10 – 80 °С описывается уравнением: lg p = 7,960 – 1780/T. Рассчитайте энтальпию испарения и нормальную точку кипения жидкости. 87. Давление пара жидкого нафталина С10Н8 равно 10 Торр при 85,8 °С и 40 Торр при 119,3 °С. Определите энтальпию испарения, нормальную точку кипения и энтропию испарения в нормальной точке кипения. 88. Нормальная точка кипения гексана равна 69 °С. Оцените мольную энтальпию испарения и давление пара гексана при 25° и 60 °С. 89. Давление пара (Торр) жидкого и жидкого SO2 выражается уравнением: lg p(тв) = 10,5916 – 1871,2/T и lg p(ж) = 8,3186 – 1425,7/T . Рассчитайте температуру, давление и DплH(SO2) в тройной точке. 90. Давление пара (Торр) жидкого и жидкого UF6 выражается уравнением: lg p(тв) = 10,648 – 2559,5/T и lg p(ж) = 7,540 – 1511,3/T . Рассчитайте температуру, давление и DплH(UF6) в тройной точке. 91. Давление пара над твердым Cl2 равно 352 Па при -112 °С и 35 Па при -126,5 °С, а давление пара над жидким Cl2 равно 1590 Па при -100 °С и 7830 Па при -80 °С. Определите координаты тройной точки и DHпл (Cl2). 92. Давление пара над твердым C6H6 равно 299 Па при -30°С и 3270 Па при 0 °С, а давление пара над жидким C6H6 равно 6170 Па при 10 °С и 15800 Па при 30 °С. Определите координаты тройной точки и DHпл (C6H6). 93. Давление пара над твердым SnBr4 равно 0,116 Торр при 9,8 °С и 0,391 Торр при 21 °С, а давление пара над жидким SnBr4 равно 0,764 Торр при 30,7 °С и 1,493 Торр при 41,4 °С. Определите координаты тройной точки и DHпл (SnBr4). ХИМИЧЕСКАЯ КИНЕТИКА Химическая кинетика – это учение о химическом процессе, его механизме и закономерностях протекания во времени. Законы химической кинетики позволяют: - рассчитать значение константы скорости химической реакции; - определить механизм реакции по кинетическим кривым; - прогнозировать влияние на скорость реакции температуры, концентрации реагентов, катализаторов, рН среды; - количественно охарактеризовать ферментативные реакции. Для успешного выполнения задания по химической кинетике следует проработать лекционный материал соответствующего раздела. По учебнику [1] изучить теоретический материал и разобрать решения типовых задач по задачнику [2]. В таблице 3.1 приведены основные соотношения для определения констант и времени полупревращения в реакциях различного порядка.
Таблица 3.1 Соотношения для определения констант и времени полупревращения в реакциях различного порядка
Для определения порядка реакции используют дифференциальный и интегральный методы. Дифференциальный метод основан на применении дифференциального уравнения реакции. Например, для реакции
дифференциальное уравнение имеет следующий вид:
1. Метод измерения скоростей при различной глубине превращения. Сначала проводят опыт при условии |




 (1.1)
(1.1) компонентов приведены в таблице 1.4.
компонентов приведены в таблице 1.4. , (1.2)
, (1.2) - разность суммы теплоемкостей продуктов и исходных реагентов
- разность суммы теплоемкостей продуктов и исходных реагентов , (1.3)
, (1.3) . Тогда
. Тогда  .
.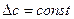 . Тогда
. Тогда  определяется по значениям теплоемкости компонентов реакционной системы при стандартных условиях (таблица 1.4) и значение
определяется по значениям теплоемкости компонентов реакционной системы при стандартных условиях (таблица 1.4) и значение  вычисляют по формуле
вычисляют по формуле . (1.4)
. (1.4) . При этом допущении необходимо учитывать температурную зависимость теплоемкости компонентов реакционной системы
. При этом допущении необходимо учитывать температурную зависимость теплоемкости компонентов реакционной системы , (1.5)
, (1.5) , (1.6)
, (1.6) . Параметры
. Параметры  рассчитываются аналогичным образом. Значения а,b, c, c/ компонентов реакции приведены в таблице 1.4.
рассчитываются аналогичным образом. Значения а,b, c, c/ компонентов реакции приведены в таблице 1.4. . (1.7)
. (1.7) необходимо учитывать температурную зависимость теплоемкости компонентов от температуры:
необходимо учитывать температурную зависимость теплоемкости компонентов от температуры: . (1.8)
. (1.8) проводят по формуле
проводят по формуле . (1.9)
. (1.9) определяют по аналогичной формуле
определяют по аналогичной формуле . (1.10)
. (1.10) )
)



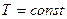





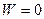

















 R .
R .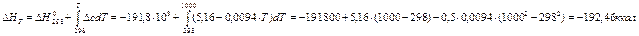 Ответ:DН1000= -192,46 ккал
Ответ:DН1000= -192,46 ккал и DSТ для реакции;
и DSТ для реакции; (г) + 2Н2О (г) = SO2 (г) + 2H2 (г)
(г) + 2Н2О (г) = SO2 (г) + 2H2 (г)

 + сТ2,
+ сТ2, 
 ,
, 
 , (2.1)
, (2.1)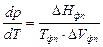 , (2.2)
, (2.2) - производная, описывающая изменение давления пара над жидкостью или твердым телом при испарении или возгонке;
- производная, описывающая изменение давления пара над жидкостью или твердым телом при испарении или возгонке;  - молярная теплота равновесного фазового перехода при температуре
- молярная теплота равновесного фазового перехода при температуре  и давлении
и давлении 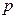 ;
;  - температура фазового перехода;
- температура фазового перехода;  - изменение объема одного моля вещества при фазовом переходе.
- изменение объема одного моля вещества при фазовом переходе.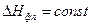 для равновесия газ-жидкость и газ-твердое тело приводит к уравнению Клаузиуса-Клапейрона:
для равновесия газ-жидкость и газ-твердое тело приводит к уравнению Клаузиуса-Клапейрона: . (2.3)
. (2.3)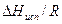 , а для системы газ-твердое тело – значение
, а для системы газ-твердое тело – значение  . Точка пересечения этих прямых дает координаты тройной точки.
. Точка пересечения этих прямых дает координаты тройной точки. . (2.4)
. (2.4) . Если оно отличается от значения 89
. Если оно отличается от значения 89  , то правило Трутона не применимо.
, то правило Трутона не применимо. . (2.5)
. (2.5) при температуре тройной точки определяют исходя из теплоты возгонки и теплоты испарения:
при температуре тройной точки определяют исходя из теплоты возгонки и теплоты испарения: . (2.6)
. (2.6) , (2.7)
, (2.7)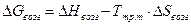 , (2.8)
, (2.8)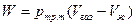 , (2.9)
, (2.9) (2.10)
(2.10)






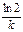













 (3.1)
(3.1) (3.2)
(3.2) >>
>>  . Получают кинетическую кривую
. Получают кинетическую кривую  . По тангенсу углов касательных к кинетической кривой в разных точках находят значения скорости
. По тангенсу углов касательных к кинетической кривой в разных точках находят значения скорости  при разных
при разных