 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Теплоемкость идеальных газов. 12
Рис. 3.5. Зависимость теплоемкости идеального газа от термодинамического процесса: n=0 — изобарный процесс с=сp ; n=1 — изометрический процесс
Так как теплоемкость тела с при изменении температуры на одно и тоже количество градусов прямо пропорциональна количеству тепловой энергии
Здесь R, Если умножить обе части этого равенства на киломольную массу газа
Здесь Рассмотрим теплоемкость идеальных газов. Из курса физики известно, что киломольная теплоемкость идеального газа при постоянном объеме равна,
Здесь число 3 означает количество поступательных степеней свободы молекул (у всех молекул независимо от числа атомов в молекуле оно одинаково); i — число вращательных степеней свободы молекул. Эта формула получена без учета колебательного движения атомов в молекуле газа и может быть использована при небольших температурах газов Задача 3.1. Пояснить, почему у одноатомной молекулы i=0, у двухатомной i=2, у трехатомной молекулы и молекулы с числом атомов, больше трех, i=3. Зная cVm, легко найти cV из равенства
Величину cp теперь можно определить из уравнения Майера
Теплоемкость смеси газов Теплоемкость смеси газов может быть определена из условия, что количество тепловой энергии Q, которой смесь газов обменивается с внешней средой, равно сумме тепловых энергий
Отсюда
Так как все газы в смеси нагреваются одинаково
Теплоемкость смеси может быть так же выражена через объемные доли
Замечая, что
Все соотношения, полученные в этом параграфе, справедливы для равновесного состава смеси газов. Энтропия. Одним из функций состояния термодинамической системы является энтропия. Энтропией называется величина определяемая выражением: dS = dQ / T. [Дж/К] (3.1) или для удельной энтропии: ds = dq / T. [Дж/(кг·К)] (3.2)
S = f1(P,V) ; S = f2(P,T) ; S = f3(V,T) ; (3.3) или для удельной энтропии: s = f1(P,υ) ; s = f2(P,T) ; S = f3(υ,T) ; (3.4) Так как энтропия не зависит от вида процесса и определяется начальными и конечными состояниями рабочего тела, то находят только его изменение в данном процессе, которые можно найти по следующим уравнениям: Ds = cv·ln(T2/T1) + R·ln(υ 2/υ 1) ; (3.5) Если энтропия системы возрастает (Ds > 0), то системе подводится тепло.
12 |




 ; n=k адиабатный процесс с=0;
; n=k адиабатный процесс с=0; 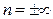 — изохорный процесс с=сV.
— изохорный процесс с=сV. , которой тело обменивается с внешней средой (см. 3.20), то для большинства тела cp>cV. Впервые это показала Р. Майер (1841 г.) для газов. Он установил, что cp и cV для газов удовлетворяют соотношению, которое носит его имя:
, которой тело обменивается с внешней средой (см. 3.20), то для большинства тела cp>cV. Впервые это показала Р. Майер (1841 г.) для газов. Он установил, что cp и cV для газов удовлетворяют соотношению, которое носит его имя: (3.22)
(3.22) — газовая постоянная, численно равная количеству теплоты, которое идет на работу расширения газа, нагреваемого на 1 градус при постоянном его давлении (p=const).
— газовая постоянная, численно равная количеству теплоты, которое идет на работу расширения газа, нагреваемого на 1 градус при постоянном его давлении (p=const).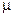 , то получим соотношение (уравнения) Майера для 1 киломоля газа
, то получим соотношение (уравнения) Майера для 1 киломоля газа (3.23)
(3.23) — газовая постоянная одного киломоля газа, т. е. универсальная газовая постоянная.
— газовая постоянная одного киломоля газа, т. е. универсальная газовая постоянная. (3.23)
(3.23)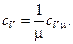 (3.25)
(3.25)
 , которыми обмениваются со средой компоненты смеси:
, которыми обмениваются со средой компоненты смеси:

 , то массовая теплоемкость смеси c выражается через массовые доли компонентов смеси
, то массовая теплоемкость смеси c выражается через массовые доли компонентов смеси 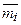 и их массовые теплоемкости ci по формуле
и их массовые теплоемкости ci по формуле (3.26)
(3.26) и др. доли (
и др. доли (  ,
,  ) с учетом соотношений (3.9)
) с учетом соотношений (3.9) (3.27)
(3.27) и
и  запишем соотношение для киломольных теплоемкостей
запишем соотношение для киломольных теплоемкостей (3.28)
(3.28)