 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Найпростіша цілочислена арифметика 12
61. Дано дійсне число х. Одержати цілу частину числа х; потім-число х, округлене до найближчого цілого; потім-число х без дробових цифр. 62. Визначити, чи є дане ціле число парним. 63. Визначити, чи вірно, що при розподілі ненегативного цілого числа а на позитивне ціле число b виходить залишок, рівний одному з двох заданих чисел r чи s 64. Дано натуральне число п (n > 99). Визначити число сотень у ньому. 65. - Дане натуральне число п (п < 99). З'ясувати, чи вірно, що n2 дорівнює кубу суми цифр числа п. 66. Дано цілі числа k, т, дійсні числа х, у, z. При k < 67. Дано натуральне число п (п <100). а) Скільки цифр у числі n? б) Чому дорівнює сума його цифр? в) Знайти останню цифру числа п. г) Знайти першу цифру числа п. д) У припущенні, що n >10, знайти передостанню цифру числа п. 68. Дано натуральне число n (n < 9999). а) чи e це число паліндромом (перевертнем) з обліком чотирьох цифр, як, наприклад, числа 2222, 6116, 0440 і т.д.? б) чи Вірно, ч1об це число містить рівно три однакові цифри, як, наприклад, числа 6676, 4544, 0006 і т. д . в) чи вірно, що всі чотири цифри числа різні ? 69. Годинна стрілка утворить кут 70. Дано цілі числа т, п (0 < т <12, 0 < п < 60), що вказують момент часу: «m годин, п хвилин». Визначити найменший час (число повних хвилин), що повинне пройти до того моменту, коли годинна і хвилинна .стрілки на циферблаті а) збіжаться; б) розташуються перпендикулярно друг до друга. 71. Дано дійсне число а. Обчислити f(а), де f-періодична функція з періодом 1.5, що збігається на відрізку [0, 1.5]: а) з функцією х3—2.25x ; б) з функцією, графік якої зображений на мал. 4.
72. Дано дійсне число а. Обчислити f(а), де f-періодична функція з періодом 2, що збігається на відрізку [—1, 1]: а) з функцією б) з функцією, графік якої зображений на мал. 5. 73. Дано цілі числа k, I. Якщо числа не рівні,тозамінити кожне з них тим самим числом, рівним більшому з вихідних, а якщо рівні, то замінити числами-нулями. 74. Дано натуральне число п (п < 100), що визначає вік людини (у літах). Дати для цього, числа найменування «рік», «року» чи «років»: наприклад, 1 рік, 23 року, 45 років і т.д. , 75. Довести, що будь-яку цілочисленну грошову суму, велику 7руб., можна виплатити без здачі трішками і п'ятірками. Для даного п > 7 знайти такі цілі ненегативні а і b, що За + 5b == п. 76. Поле шахівниці визначається парою натуральних чисел, кожне з який не перевершує восьми : перше число-номер вертикалі (при рахунку ліворуч праворуч),. друг-номер горизонталі (при рахунку знизу нагору). Дані натуральні числа r, l, т, n, кожне з який не перевищує восьми. Потрібно: а) З'ясувати, чи є полючи (k, I) і (т, п) полями одного кольору. б) На поле (k, I) розташований ферзь. Чи загрожує він полю (т, n)? . в) Аналогічно б), але ферзь заміняється на коня. г) З'ясувати, чи можна з полючи {k, I) одним ходом тури потрапити на поле (т, п). Якщо ні, то з'ясувати, як це можна зробити за два ходи (указати поле, на яке приводить перший хід). д) Аналогічно г), але тура заміняється на ферзя. е) Аналогічно г), але тура заміняється на слона. Передбачається, що зазначені полючи мають один і той самий колір. Найпростіші цикли 77. Дано натуральне число п. Обчислити: а) б) n! в) г) д) e) 78. Дано дійсне число а, натуральне число л. Обчислити; а) б) а(а + 1)...(а + n -1); в) г) д) а (а - n)(а - 2n). ..(а - n2). 79. Обчислити ( l+sin0.1 )( l-sin 0.2)……(l + sin 10). 80. Дано дійсне число n:. Обчислити
81. Дано дійсні числа х , а, натуральне число п обчислити
82. Дано дійсне число х. Обчислити:
83. Дано дійсне число а. Знайти: а) серед чисел б) таке найменше п , що 84. Дано натуральне n, дійсне х. Обчислити: а) sin х + sin2 х + ... + sinn х; б)
85. Дано дійсні числа a, h, натуральне число п. Обчислити f(a)+2f(a+h)+2f{a+2h)+ ......+2f(a+(n—1)h)+f(a+nh), де f(x)=(x2+ l)cos2x. 86. Дано натуральне число п. а) Скільки цифр у числі, n? б) Чому дорівнює сума його цифр? в) Знайти першу цифру числа п. г) Знайти знакочергуючу суму цифр числа n (нехай запис п у десятковій системі є 87. Дані натуральні числа п, т. Одержати суму m останніх, цифр числа п. 88. Дано натуральне число п. а) З'ясувати, чи входить цифра 3 у запис числа п2. б) Поміняти порядок цифр числа п на зворотний. в) Переставити першу й останню цифри числа п. г) Приписати по одиниці в початок і в кінець запису числа п 89. Алгоритм Евкліда перебування найбільшого загального дільника (НОД) ненегативних цілих чисел заснований на наступних властивостях цієї величини. Нехай т і п - одночасно не рівні нулю цілі ненегативні числа і нехай т>п. Тоді, якщо n = 0, то (НОД) (п, т)=т, а якщо п=0, то для чисел т, п і r, де r –залишок від розподілу т на п , виконується рівність НОД (m, п} =НОД(n, r). Наприклад, НОД(15, 6)=НОД(6, 3)= = НОД(3, 0)=3. Дано натуральні числа п , т. а) Використовуючи алгоритм Евкліда, знайти найбільший загальний дільник п і т. б) Знайти найменше загальне кратне п і т, (Як тут може допомогти алгоритм Евкліда?) 90. Дано натуральні числа т і п. Знайти такі натуральні р і q, що не мають загальних дільників, що p/q = m/n. 91. Нехай
Дано натуральне число п . Отримати 92.Нехай
Дано натуральне п (n > 4). Одержати 93. Нехай
Дано дійсні q, r, b, c, d, натуральне п ( п >2). Одержати 94. Нехай
95.Нехай a0=a1=1; ai=ai-2+ai-1/2i-1; i=2,3,….. Знайти добуток а0*а1*а2.....а14
96. Нехай
98. Нехай
99. Нехай
Данні дійсні u ,v натуральні n. Знайти
100. Нехай
Знайти
101 Дані позитивні дійсні числа а, х , е. У послідовності
знайти перший , член
102. Нехай
Знайти перший член 103. Нехай
Дано дійсне a > 0. Знайти перший член 104. Дано дійсне a >0. Послідовність
Знайти перший член
Обчислити для знайденого значення 105. Дано натуральне число л, дійсне число х. Обчислити: а) б) 106. Дано дійсні числа а, b, натуральне число п (b > а). Одержати (f1 + ... + fn) h, де
107. Дано ціле число m > 1. Одержати найбільше ціле k, при якому 108.. Дане натуральне число п. Одержати найменше ціле виду 109. Дано натуральне число п. Обчислити 1*2+2*3*4+…+n*(n+1)*…*2n 110. Обчислити
111. Дано дійсне число x = О. Обчислити
……………….
112. Дано цілі числа n, k (n>k>0). Обчислити
113./'Нехай п - дійсне число і нехай n!! означає 1 3 5……п для непарного п і 2 4 ..... п для парного п. Для заданого натуральних я обчислити: а) a!!; b) 114. Обчислити: a) в) д) ж) 115. Дано натуральне число п. Обчислити: а) в) д) ж)
116. Дано натуральне число п, дійсне число х Обчислити: а) в) д)
117. Дано натуральне число п. Обчислити добуток перших п співмножників: а) б) 118 Обчислити а) послідовно зліва направо; б) послідовно зліва направо обчислюються потім друге значення віднімається з першого; в) послідовно праворуч ліворуч; г) послідовно праворуч ліворуч обчислюються суми, написані в б), потім-віднімання. Чому при обчисленнях на обчислювальній машині кожним з цих способів виходять різні результати? 119. Обчислити нескінченну суму з заданою точністю e (е > 0). Вважати, що необхідна точність досягнута, якщо обчислена сума декількох перших доданків і черговий доданок виявився по модулі менше, ніж е , - ці і всі наступні доданки можна вже не враховувати. обчислити:
а) в) д) 12 |



 , k = т2 чи k > т2 замінити модулем відповідно значення х, у чи z, а два інших значення зменшити на 0.5.
, k = т2 чи k > т2 замінити модулем відповідно значення х, у чи z, а два інших значення зменшити на 0.5. із променем, що проходить через центр і через крапку, що відповідає 12 годинник на циферблаті, 0<
із променем, що проходить через центр і через крапку, що відповідає 12 годинник на циферблаті, 0< 

 ;
;
 ;
; ;
; ;
;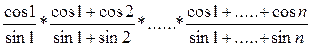 ;
; ;
; ;
; ;
;


 …..перше більше а;
…..перше більше а;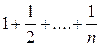 >a
>a
 в) sin x + sin sin x + ... + sin sin.. .sin x.
в) sin x + sin sin x + ... + sin sin.. .sin x. ; знайти .
; знайти . 
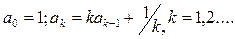








 i=3,4..
i=3,4..




 i=4,5,…
i=4,5,…
 ,утвореної за законом
,утвореної за законом i=1,2……,
i=1,2……, для якого виконана нерівність
для якого виконана нерівність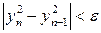
 k=1,2…..
k=1,2….. .
. k=1,2..
k=1,2.. , для якого виконано
, для якого виконано 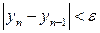
 ... утворена за законом
... утворена за законом
 .
.
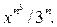 .
. 
 i=1,2,…,n.
i=1,2,…,n. .
. , що перевершує п.
, що перевершує п.





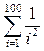 ; б)
; б) 
 г)
г) 
 е)
е) 
 з)
з) 
 б)
б) 
 г)
г) 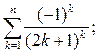
 е)
е) 

 б)
б) 
 г)
г) 
 е)
е) 


 слідуючими чотирма способами:
слідуючими чотирма способами: і
і 
 б)
б) 
 г )
г ) 
 е)
е) 