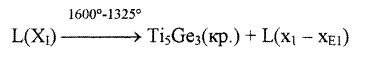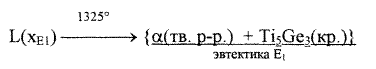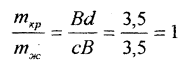ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Описание граней кристаллических решеток. 12
Пример 1. Описать грань А/В/С.
Дано: x, y, z – оси, АВС – единичная грань, А/В/С – грань, которую надо описать. Решение: Обозначим параметры грани следующим образом: (А/О:АО):(В/О:ВО):(СО:СО). Описаниеграни строится не на отношении параметров, а на отношении индексов Миллера (h : k : l) – величин обратных параметрам:
Символ грани (индексы Миллера)
Пример 2. Описать грань АВС/ кубической решетки.
Дано: x, y, z – оси, АВС/ – грань, расположенная слева от осей, которую необходимо описать. Решение: Обозначим параметры грани следующим образом (АО:АО):(ВО:ВО):(С/О:СО). Построим описание грани с помощью индексов (h:k:l).
Пример 3. Описать грань АСВЕ кубической решетки.
Дано: x, y, z – оси, грань АСВЕ пересекает оси y и z в точках В, C, ось x – бесконечности (∞). Решение: Обозначим параметры грани (∞:АС):(ОС:ОС):(ОВ:ОВ). Описание грани строится на индексах (h:k:l).
Расчет основных размеров элементарных ячеек кубической системы Пример 4. Определить число n узлов, приходящихся на одну элементарную ячейку в гранецентрированной кубической решетке. Решение:
Выделим элементарную ячейку в кубической решетке и определим, скольким соседним элементарным ячейкам принадлежит тот или иной узел выделенной ячейки. В этой ячейке имеются узлы двух типов: А (находящиеся в вершинах куба) и В (находящиеся на гранях куба в точке пересечения диагоналей).
Узел А принадлежит одновременно восьми элементарным ячейкам. Следовательно, в данную ячейку узел А входит с долей 1/8. Узел В входит одновременно только в две ячейки и, следовательно, в данную ячейку узел В входит с долей 1/2. Если учесть, что число узлов типа А в ячейке равно восьми, а число узлов типа В равно шести, т. е. числу граней, то общее число узлов, приходящихся на одну элементарную ячейку в гранецентрированной решетке,
n = (1/8)·8 + (1/2)·6 = 1 + 3 = 4 узла.
Так как число узлов равно числу атомов, то в соответствующей структуре на элементарную ячейку приходится четыре атома.
Пример 5. Определить параметр a решетки и расстояние d между ближайшими соседними атомами кристалла кальция (решетка гранецентрированная кубической сингонии). Плотность ρ кристалла кальция равна 1,55·103 кг/м3.
Решение: Параметр a кубической решетки связан с объемом элементарной ячейки соотношением V=a3. С другой стороны, объем элементарной ячейки равен отношению молярного объема к числу элементарных ячеек в одном моле кристалла: V=Vm/Zm. Приравняв правые части приведенных выражений для V, найдем а3 = Vm/Zm. Молярный объем кальция Vm =М/ρ , где ρ— плотность кальция; М — его молярная масса. Число элементарных ячеек в одном моле
Zm=NA/n
где п — число атомов, приходящихся на одну ячейку. Тогда, а3= nM/ ρ NA Отсюда,
Подставим значения величин n, M, ρ и NA, учитывая, что n=4 (см. предыдущий пример). Произведя вычисления найдем а=556 пм. . Расстояние d между ближайшими соседними атомами находится из простых геометрических соображений, ясных из рис.
Подставив в это выражение найденное ранее значение а, получим 393 пм.
Пример 4. Определите, к какому структурному типу кристаллической решетки кубической системы (тип СsС1, NaCl или ZnS) относится оксид бария BaO, если известны радиусы ионов и плотность вещества: Rкат =1,36·10-10м, R анион =1,40·10-10м, ρ = 6,022 г/см3, укажите координационное число ионов. Решение: Перечисленные структурные типы отличаются числом формульных единиц в элементарной кубической ячейке (соответственно 1, 4, 4) и соотношением параметра элементарной ячейки (ребра куба) а и межионного расстояния (кратчайшего расстояния) d. По исходным данным можно определить межионное расстояние d и затем рассчитать параметр элементарной ячейки а для всех трех вариантов. По вычисленному параметру элементарной ячейки рассчитываем плотность вещества и сравниваем с приведенным в условии задачи значением. Определяем структурный тип по совпадению рассчитанного и заданного значения плотности. Определим межионное расстояние d = Rкат + R анион =1,36 + 1,40 = 2,76·10-10м. Рассчитаем параметр элементарной ячейки а: для структурного типа CsCl (объемноцентрированный куб) - а = 2d/Ö3 = 2·2,76/1,732 = 3,187·10-10м; для структурного типа NaCl (примитивный куб) - а = 2d = 2·2,76 = 5,52·10-10м; для структурного типа ZnS (алмазоподобная решетка) - а=4d/Ö3= 4·2,76/1,732 = 6,374·10-10м. Рассчитываем плотность вещества по формуле r = m/V = (ZM)/(NA a3), где Z – число формульных единиц, M – молярная масса вещества, NA – число Авогадро, a3 – объем кубической элементарной ячейки: для структурного типа CsCl - r = 1·0,15334кг/моль / [6,02·1023моль-1· (3,187·10-10м )3] = 7864 кг/м3=7,864 г/см3; для структурного типа NaCl - r = 4·0,15334кг/моль / [6,02·1023моль-1· (5,52·10-10м )3] = 6053 кг/м3 = 6,053 г/см3; для структурного типа ZnS - r = 4·0,15334кг/моль / [6,02·1023моль-1· (6,374·10-10м )3] =2369 кг/м3 =2,369 г/см3. Рассчитанное значение плотности совпадает с заданным только в случае структурного типа NaCl, для которого координационные числа катиона и аниона равны 6.
ЗАДАНИЕ 5 Определите формулу соединения, кристаллизующегося в кубической сингонии, по следующим данным (число атомов в формуле только целое, Z –число формульных единиц в элементарной ячейке)
Решение: Масса кристалла с одной стороны m=rV, с другой стороны m=ZM/NA Приравняв эти два выражения, получим ZM/NA=rа3. Тогда M=rа3 NA/Z. Подставив численные значения, получим М≈367г/моль. М(Ti)=48г/моль M(Br)=80 г/моль
Формула соединения: TiBr4
Многовариантные задания по теме « КРИСТАЛЛИЧЕСКОЕ СОСТОЯНИЕ ВЕЩЕСТВА
Задание 2 (для вариантов 1-10) Определите, используя приведенные ниже экспериментальные данные, структурный тип кристаллической решетки, в которой кристаллизуется данное вещество (структурный тип NaCl или CsCl), рассчитайте ионный радиус катиона, изобразите элементарную ячейку, укажите координационное число.
\ Задание 4. Определите формулу соединения, кристаллизующегося в кубической сингонии, по следующим данным (число атомов в формуле только целое, Z –число формульных единиц в элементарной ячейке):
ТЕМА 3. ФАЗОВЫЕ ДИАГРАММЫ
Пример 6. Условие задачи: Проанализировать диаграмму состояния двухкомпонентной системы. Задание 1. Указать фазовый состав всех областей диаграммы состояния (обозначенных цифрами в кружке). Указать химические соединения в предложенной системе и записать реакции, по которым они образуются. Задание 2. Провести анализ фазовых превращений для сплавов указанного состава и построить для них кривые охлаждения. Задание 3. Определить качественно и количественно фазовый и химический состав системы при заданной температуре. Масса сплава 100 г.
Решение задачи: Задание 1 Данная диаграмма содержит 13 областей различного фазового состава. На рис. 1 эти области пронумерованы числами 1,2,3...,13. Область 1 соответствует температуре выше ликвидуса. В этой области система представляет собой гомогенный жидкий расплав титана и германия. В данной системе образуется химическое соединение, отвечающее формуле Тi5Gез и плавящееся конгруэнтно (т. е. без разложения). Это соединение кристаллизуется из расплава при T=1980 °С. В связи с наличием соединения Тi5Gез всю диаграмму состояния Тi - Gе можно рассматривать как две диаграммы: Диаграмма 1 - Тi (компонент А) - Тi5Gез (компонент В) Диаграмма 2 - Тi5Gез (компонент А) - Ge(компонент В). Диаграмма 1 содержит четыре фазовые области. Область 2 - гомогенная система твёрдых растворов соединения Тi5Gез в титане (α- твёрдый раствор). Максимальная растворимость соответствует содержанию германия - 8 ат.% при температуре 1325 °С. Заметной растворимости титана в Тi5Gез не наблюдается. Области 3 и 4 - области сосуществования двух фаз - расплава и кристаллов. Причём в области 3 твёрдая фаза представляет собой кристаллы твёрдого раствора соединения Тi5Gез, а в области 4 -кристаллы соединения Тi5Gез. В системе, содержащей 15 ат.% германия и 85 ат.% титана (точка Е1) при температуре 1325 °С происходит эвтектическая реакция:
Фазовая область 5 представляет собой эвтектику Е1 образующуюся по реакции (1) - мелкодисперсную смесь кристаллов α-твердого раствора и кристаллов соединения Тi5Gез. Диаграмма 2 содержит 8 фазовых областей. Область 6 - двухфазная. В ней сосуществуют жидкий расплав и кристаллы соединения Тi5Gез. При температуре 1650 °С в системе происходит перитектическая реакция, в результате которой образуется соединение состава Тi6Gе5:
Соединение Тi6Gе5 плавится инконгруэнтно. Область 7 - двухфазная. В ней сосуществуют жидкий расплав и кристаллы соединения Тi6Gе5. При температуре 1075 °С происходит перитектическая реакция, в результате которой образуется соединение состава:
Соединение TiGe2 плавится инконгруэнтно. Точки P1 и P2 (составы хр1 и хp2) соответствуют приведённым выше реакциям (2) и (3). Область 8 - двухфазная. В ней сосуществуют жидкий расплав и кристаллы соединения TiGe2. Область 9 - двухфазная. В ней сосуществует жидкий расплав и кристаллы β-твёрдого раствора титана в германии. Область 10 - однофазная (гомогенная) область β-твёрдых растворов титана в германии. Область 11 - двухфазная, состоящая из кристаллов Ti5Ge3, окружённых твёрдой фазой Т16Gе5, образующейся по реакции (2). Область 12 - двухфазная, состоящая из кристаллов Т16Gе5, окружённых твёрдой фазой TiGe2, которая образуется по реакции (3). При температуре 900 °С в системе происходит эвтектическая реакция:
Область 13 представляет собой эвтектику Е2 - мелкодисперсную смесь кристаллов соединения TiGe2 и β-твёрдого раствора титана в германии.
Задание 2. Сплав состава I содержит 20 ат.% Gе и 80 ат% Тi (состав изображён на рисунке вертикальной чертой I). Кристаллизация сплава I начинается в точке при температуре tа=1600°С. Первый этап кристаллизации происходит в интервале температур от tа до tВ=1325°С в двухфазной области и являются одновариантным фазовым превращением (число степеней свободы С=К-Ф+1= 2-2+1). Поэтому на кривой охлаждения сплава I в указанном интервале температур уменьшается скорость охлаждения (Скорость охлаждения (наклон кривых) выбирается произвольно, так как необходимо только отразить изменение её в результате протекающих в системе фазовых превращений). Реакция первичной кристаллизации выражается уравнением
Второй этап кристаллизации сплава I - эвтектическая реакция. Это нонвариантное фазовое превращение (С=2-3+1=0), происходящее при постоянной температуре 1325°С:
Этот процесс отражается на кривой охлаждения горизонтальным участком. На этом фазовые превращения в сплаве I заканчиваются. В результате кристаллизации сплава I образуется структура, содержащая две составляющих: - кристаллы соединения Ti5Ge3, выделившиеся на первом этапе кристаллизации ; - окружающая эти кристаллы эвтектика, состоящая из смеси мелких кристаллов Ti5Ge3 и α-твёрдого раствора германия в титане. Эвтектика образуется на втором этапе кристаллизации. Сплав II содержит - 43 ат.% Gе и 57 ат.% Тi. Кристаллизация этого сплава также происходит в два этапа. На первом этапе в интервале температур от tc=1900° С до температуры перитектики 1 (Р1) tр1=1650°С реализуется одновариантное фазовое превращения (С=2-2+1=1) по реакции:
Второй этап кристаллизации - перитектическая реакция - нонвариантное превращение (С=2-3+1=0). Ему соответствует горизонтальный участок на кривой охлаждения (см, рисунок ). Сплав состава xп является заперитектическим (при температуре перитектики tр1=16500С образовавшиеся кристаллы Тi5Gез находится в избытке по отношению к жидкой фазе L (xd) Поэтому при перитектической реакции образуется новая твёрдая фаза, но первичные кристаллы полностью не растворяются:
В результате сплав II приобретает двухфазную структуру, состоящую из остаточных кристаллов Ti5Ge3, окружённых образовавшейся твёрдой фазой кристаллов Тi6Ge5. На этом превращения в сплаве II заканчиваются. Сплав III содержит 75 ат.% Gе и 25 ат% Ti. Первый этап кристаллизации этого состава совершенно аналогичен кристаллизации сплавов I и II. Он происходит в интервале температур от t1≈220°С до tk=1075°С является одновариантным превращением и заканчивается образованием кристаллов соединения Тi6Gе5 и расплава состава хк. I этап:
Второй этап кристаллизации - нонвариантное перитектическое превращение. Причём сплав III - доперитектический (при температуре перитектики Р2, равной 1075°С находится в избытке по отношению к кристаллам Ti6Ge5). Поэтому при перитектической реакции кристаллы Ti6Ge5полностью растворяются в расплаве с образованием новой твёрдой фазы ТiGe2 , а расплав полностью не исчезнет. II этап:
На третьем этапе из остаточного расплава L (xk) в интервале температур 1075 - 900°С будут выделяться кристаллы ТiGe2 (одновариантное превращение), но полной кристаллизации не произойдёт: состав жидкой фазы изменится, но полностью она не исчезнет. Ш этап:
Полная кристаллизация сплава Ш происходит по эвтектической ре акции (эвтектика Е2). IV этап:
Таким образом, кристаллизация сплава III заканчивается образованием структуры, имеющей две составляющие: - кристаллы соединения ТiGе2 , образовавшиеся на втором и третьем этапах кристаллизации (они не различимы между собой); - эвтектика, окружающая кристаллы ТiGе2 и представляющая собой мелкодисперсную смесь кристаллов ТiGе2 β-твёрдого раствора титана в германии.
Задание 3 Для определения качественного и количественного состава фаз в сплавах I и II выделим участок диаграммы состояния Тi - Gе , содержащий фигуративные точки А и В в большем масштабе (рис. 2). Точка А соответствует сплаву I, содержащему 20 ат.% германия, находящегося при температуре 1500°С; точка В - сплаву II, содержа- щего 43 ат.% германия при t=17000С. Обе фигуративные точки расположены в двухфазных областях, в которых существует жидкая фаза (расплав) и твёрдая фаза (кристаллы). Для определения химического состава фаз через фигуративную точку А проводим коноду аАb. Проекция точки пересечения коноды с линией ликвидус (точка а) на ось состава укажет химический состав жидкой фазы хж, а проекция тачки пересечения коноды с линией солидус ( точка b) - состав твёрдой фазы хтв. В нашем случае для сплава I: Состав сплава: 18 ат.% германия 72 ат. % титана Состав твёрдой фазы: кристаллы соединения Тi5Gез. Для определения количественного соотношения между фазами воспользуемся правилом отрезков (правилом рычага). Согласно этому правилу:
Где mтв и mж - массы твёрдой и жидкой фаз соответственно; аА и Аb - длины отрезков коноды ( в единицах длины). В нашем случае:
Масса сплава
Тогда уравнение принимает вид:
Откуда
Соответственно масса расплава mж = М - mкр = 100 - 14,3 = 85,72 г, Таким образом, 100 г сплава I при t = 1500°С состоит из 85,7 г расплава состава 18 ат.% германия и 78 ат.% титана, а также 14,3 г кристаллов соединения Ti5Ge3 Аналогично, для сплава II при t = 1700°С: Состав расплава (проекция точки d коноды сВd): 50 ат.% германия и 50 ат.% титана. Состав твёрдой фазы (проекция точки с) кристаллы соединения Тi5Ge3. Правило отрезков для сплава II:
Откуда mкр = mж == 100/2 = 50 г Таким образом, сплав II при t= 1700°С состоит из равных количеств расплава, содержащего по 50 ат.% германия и титана, и кристаллов соединения Ti5Ge3
.
12 |






 (112).
(112).
 Если грань пересекает оси в отрицательном направлении, то над индексами ставятся черточки.
Если грань пересекает оси в отрицательном направлении, то над индексами ставятся черточки.
 Символ грани АСВЕ (011).
Символ грани АСВЕ (011).