 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Послідовність виконання роботи 3 страница
Запишемо рівняння у вигляді xi+1=(5-cos(xi))/2 і наведемо початкове значення кореня х=0,5 .
2.3 Графічний алгоритм
Графічний алгоритм показаний на рис. 9.1.
2.4 Таблиця ідентифікації змінних
2.5 Програма мовою Pascal та результати обчислень
Program IT{ітерації}; Var y,x,e,t:real; n:integer; Begin x:=0.5; e:=0.0001; n:=0; repeat y:=(5-cos(x))/2; t:=abs(x-y); x:=y; n:=n+1; until t<e;
ні
так
Рисунок 9.1 – Графічний алгоритм
writeln('Результати обчислень: '); writeln(' Корінь рівняння =',y:6:3); writeln(' Кількість ітерацій =',n); end.
Результати обчислень: Корінь рівняння = 2.995 Кількість ітерацій = 7
3 Контрольні запитання 1. Яка відмінність ітераційного циклу від циклу з регулярною зміною аргументу? 2. Які дані необхідні для організації циклу? 3. Як одержати ітераційну формулу для застосування методу ітерацій? 4. Яка умова закінчення ітераційних обчислень? 5. Як отримати кількість виконаних ітераційних циклів? 6. Який оператор керує виходом з циклу? 7. Побудуйте програму, використавши структуру циклу з передумовою. Варіанти завдань наведені в таблиці 9.1 . Примітка. При використанні методу Ньютона необхідно визначити, яка з крайніх точок інтервалу ізоляції буде рухомою. Таблиця 9.1 –Варіанти завдань
Продовження таблиці 9.1
ЛАБОРАТОРНА РОБОТА № 10 Тема: Turbo Pascal. Алгоритми і програми для обробки одновимірних масивів.
Мета: Формування умінь створення програм, які містять одновимірні масиви алгоритмічною мовою високого рівня Pascal.
Теоретичні відомості Масив – це впорядкований скінченний набір даних одного типу, які зберігаються в послідовно розташованих комірках оперативної пам’яті і мають спільну назву. Назву масиву задає користувач. Масив складається з елементів. Кожний елемент має індекси, за якими його можна знайти в масиві. Кількість індексів елементів визначає розмірність масиву. Елементи масиву позначають іменем масиву, а у квадратних дужках пишуть значення індексу елемента масиву. Щоб опрацювати елементи масиву використовують команду циклу for (чи while або repeat…until).
Хід роботи 2.1 Постановка задачі Дано одновимірний масив С, який складається з 15 елементів. Замінити одиницями елементи масиву, які знаходяться після найменшого елементу.
2.2 Графічний алгоритм показаний на рис. 10.1.
2.4 Програма мовою Pascal та результати обчислень
Program OM{одновимірні_масиви}; Var min:real; i,n:integer; c:array[1..15] of real; Begin writeln('Введіть елементи масиву'); for i:=1 to 15 do begin writeln('c[',i,']='); read(c[i]) end; writeln('Вихідні дані :'); for i:=1 to 15 do write(' ',c[i]:6:3); min:=c[i]; for i:=2 to 15 do if c[i]<min then begin min:=c[i]; n:=i end; for i:=n+1 to 15 do c[i]:=1; writeln('Результати розрахунку :'); for i:=1 to 15 do writeln('c[',i,']=',c[i]:6:3); end.
ні
так
Рисунок 10.1 – Графічний алгоритм Вихідні дані : с[1]=5.200 с[2]=0.150 с[3]=4.000 с[4]=61.000 с[5]=-3.500 с[6]=5.000 с[7]=9.000 с[8]=12.000 с[9]=-4.200 с[10]=18.000 с[11]=100.000 с[12]=41.000 с[13]=8.000 с[14]=-1.320 с[15]=15.000
Результати розрахунку : с[1]=5.200 с[2]=0.150 с[3]=4.000 с[4]=61.000 с[5]=-3.500 с[6]=5.000 с[7]=9.000 с[8]=12.000 с[9]=-4.200 с[10]=1.000 с[11]=1.000 с[12]=1.000 с[13]=1.000 с[14]=1.000 с[15]=1 .000
3 Контрольні запитання
1. Як оголошуються масиви ? 2. Для чого оголошуються масиви? 3. Як записується елемент масиву? 4. Які способи введення і виведення одновимірних масивів ви знаєте? 5. Як визначається номер індексу, який заданий арифметичним виразом? 6. Охарактеризуйте основні атрибути масиву. 7. Який алгоритм пошуку найменшого елемента масиву? 8. Що таке масив?
Варіанти завдань наведені нище: 10.1. Дано одновимірний масив Х, який складається з 12 елементів, обчислити
Результат вивести у вигляді масиву у . 10.2. Обчислити значення виразу
Аргумент х змінюється від 0,8 до 1,7 з кроком 0,05 (радіан). Результати обчислень вивести у вигляді масиву. 10.3. Дано координати точок х1, y1, x2, y2,...,x20,y20 та рівняння прямої y=ax+b; b= -2,1; a=1,34. Сформувати і вивести на друк масив С, який складається з ординат точок, що належать цій прямій, і визначити їх кількість.
10.4. Дано координати точок х1, y1, x2, y2,...,x12,y12. Визначити, чи належать точки заштрихованій фігурі (рис.6.1). 10.5. Дано координати точок х1, y1, x2, y2,...,x15,y15. Сформувати і вивести на друк два масиви: масив А - ординати точок, які знаходяться в першій чверті, і їх кількість; масив В - абсциси точок, які знаходяться в третій чверті, і їх кількість. 10.6. Дано координати точок х1, y1, x2, y2,...,x15,y15. Якщо точка попадає в площину, обмежену колом х2+y2=R2 , то вивести на друк координати цієї точки і повідомлення “ТОЧКА В ПЛОЩИНІ”; якщо точка за межами кола, то вивести на друк координати точки і повідомлення “ТОЧКА ЗА МЕЖАМИ”. R=15. 10.7. Дано цілочисловий одновимірний масив, який складається з 16 елементів. Знайти парні елементи масиву, які більші числа А, і їх кількість. Число А ввести з клавіатури. 10.8. Дано одновимірний масив P, який складається з 16 елементів. Знайти номери тих елементів, модуль яких дорівнює заданому числу А. Число А ввести з клавіатури. 10.9. Дано цілочисловий одновимірний масив T, який скла-дається з 25 елементів. Сформувати два масиви: перший, який складається з додатних елементів масиву T, другий - з від’ємних. 10.10. Дано одновимірний масив P, який складається з 30 елементів. Знайти мінімальний елемент і його порядковий номер. Всі числа, розташовані перед мінімальним елементом, поділити на нього. Вивести на друк заданий і новоутворений масиви. 10.11. Дано одновимірний масив P, який складається з 32 елементів. Обчислити значення функції для від’ємних елементів масиву і підрахувати їх кількість.
10.12. Обчислити елементи масиву T, який складається з 8 елементів:
10.13. Дано одновимірний масив В, який складається з 15 елементів. Сформувати вектор А, першим елементом якого є найменше число, а наступні елементи вектора А - числа, розташовані за найменшим елементом масиву В. 10.14. Дано одновимірний масив Х, який складається з 15 елементів. Визначити півсуму найбільшого і найменшого елементів масиву. 10.15. Дано одновимірний масив С, який складається з 16 елементів. Поміняти місцями мінімальний і максимальний елементи. 10.16. Дано одновимірний масив В, який складається з 12 елементів. Сформувати вектор С, що повинен складатися з елементів вектора В, розташованих перед максимальним елементом. Вивести на друк вектори В і С. 10.17. Дано цілочисловий одновимірний масив С, який скла-дається з 15 елементів. Знайти максимальний елемент і його порядковий номер. Всі непарні числа, розташовані за максимальним елементом, звести до квадрата. Вивести на друк заданий і новоутворений масиви. 10.18. Дано три одновимірні масиви чисел A, B, C, які містять по 4 елементи. Сформувати матрицю T, стовпцями якої є дані масиви. 10.19. Дано одновимірний масив Х, розміром 20 елементів. Обчислити суму кожної пари сусідніх елементів масиву. 10.20. Обчислити значення перших п’ятнадцяти елементів геометричної прогресї, коли відомий перший елемент а=2 і її знаменник g=1,5. Наступний елемент геометричної прогресї утворюється множенням попереднього на знаменник прогресї. Примітка: для розміщення в пам’яті обчислених елементів прогресї їх слід об’явити як масив. 10.21. Дано одновимірний масив Х, розміром 15 елементів. Провести циклічний зсув елементів у масиві вправо на 2 позиції. 10.22. Дано одновимірний масив С, який складається з 12 елементів. Вилучити з масиву k-й елемент масиву (k<12). 10.23. Дано одновимірний масив Х, який складається з 12 елементів. Замінити одиницями елементи масиву, які розташо-вані після найменшого елементу. 10.24. Дано собівартості тонни нафти для 15 родовищ (від 4000 до 5500 грн. за тону). Визначити номери родовищ, для яких собівартість тонни нафти перевищує 5000 грн., і їх кількість. 10.25. Дано процентний показник виконання планового завдання кожним робітником бригади (від 60 % до 115 %). В бригаді 16 робітників. Визначити кількість і порядковий номер робітників, які виконали планове завдання на 100 % і більше. 10.26. Для умови задачі 6,25 визначити кількість робітників, які виконали планове завдання від 101 % до 110 % і більше 110 %, а також визначити їх порядкові номери. 10.27. Дано послідовність цілих чисел а1,а2,...,а16. Знайти максимальний елемент цієї послідовності і поміняти місцями максимальний елемент з першим парним числом цієї послі-довності. На друк вивести задану і перетворену послідовності чисел. 10.28. Дано послідовність цілих чисел х1,х2,...,х20. Відомо, що в ній є два однакові числа. Вивести на друк порядкові номери цих двох однакових чисел і значення цього числа. 10.29. Дано цілочисловий масив А, який складається з 12 елементів. Створити масив С, який складається з непарних чисел масиву А, полічити кількість елементів масиву С. Вивести на друк заданий і новоутворений масиви. 10.30. Дано цілочисловий масив А, який складається з 12 елементів. Створити масив С, який складається з остач ділення елементів масиву А на ціле число k (k<10). Обчислити добуток ненульових елементів масиву С. ЛАБОРАТОРНА РОБОТА № 11
Тема: Turbo Pascal. Програмування вкладених циклів.
Мета: Формування умінь створення програм, які містять вкладені цикли алгоритмічною мовою високого рівня Pascal . Теоретичні відомості Необхідно обчислити значення yi=f(z,xi), де параметр циклу z змінюється від початкового до кінцевого значення з постійним кроком z, а змінна xi(і=1,2,…,n) є елементом одновимірного масиву (дійсні числа). Для заданої функції необхідно: - скласти графічний алгоритм з використанням операторів циклу; - скласти програму з використанням операторів циклу; - вивести на друк значення функції і відповідних їм значень аргументів. Виведення аргументів виконати так, щоб один з них друкувався перед початком внутрішнього циклу; - розв’язати задачу на ЕОМ в діалоговому режимі; - проаналізувати одержані результати. Перед складанням алгоритму слід визначити кількість значень функції, які будуть одержані в результаті розв’язання задачі, т. б. кількість значень функції від кожного аргумента. Загальна кількість значень функції дорівнюватиме добутку кількостей значень всіх аргументів.
Хід роботи 2.1 Постановка задачі
Обчислити значення функції
Аргумент q змінюється від початкового значення 2,8 до кінцевого 5,4 з кроком 1.3. Змінна с являє собою одновимірний масив (с1=-1,85; с2=2,39; с3=3,65).
2.2 Графічний алгоритм показаний на рис. 11.1
ні
так
Рисунок 11.1 – Графічний алгоритм
2.3 Таблиця ідентифікації змінних
2.4 Програма мовою Pascal та результати обчислень
Program VC {Bкладені_цикли}; const a=0.65; Var m:integer; q:real; c,z: array [1..3] of real; Вegin for m:=1 to 3 do begin write('c(',m,')='); read(c[m]) end; q:=2.8; writeln('РЕЗУЛЬТАТИ РОЗРАХУНКУ:'); repeat writeln('q=',q:6:3); for m:=1 to 3 do begin z[m]:=c[m]+(exp(m)-q)/abs(1-a); writeln('z(',m,')=',z[m]:6:3,' c(',m,')=',c[m]:6:3) end; q:=q+1.3; until q>5.4 end.
РЕЗУЛЬТАТИ РОЗРАХУНКУ: q= 2.800 z(1)=-2.083 c(1)=-1.850 z(2)=15.502 c(2)= 2.390 z(3)=53.037 c(3)= 3.650 q= 4.100 z(1)=-5.798 c(1)=-1.850 z(2)=11.787 c(2)= 2.390 z(3)=45.608 c(3)= 3.650 q= 5.400 z(1)=-9.512 c(1)=-1.850 z(2)= 8.073 c(2)= 2.390 z(3)=45.609 c(3)= 3.650
3 Контрольні запитання 1. Чому не допускається перетин вкладених циклів? 2. Як визначити кількість значень функції при зміні двох аргументів? 3. Побудуйте графічний алгоритм для обчислення значень функції трьох змінних y=f(a,b,c); i=1,2,...,N; j=1,2,...,M; k=1,2,...,L. 4. Який оператор керує виходом з циклу? 5. Побудуйте програму, використавши структуру циклу з передумовою. 6. Які дані необхідні для організації циклу? 7. Що таке цикл?
Варіанти завдань наведені в таблиці 11.1 Таблиця 11.1 –Варіанти завдань
Продовження таблиці 11.1
Продовження таблиці 11.1
Продовження таблиці 11.1
ЛАБОРАТОРНА РОБОТА № 12 Тема:Turbo Pascal.Циклічні алгоритми і програми з накопиченням суми та добутку Мета:Формування умінь створення циклічних алгоритмів і програм з накопиченням суми та добутку алгоритмічною мовою високого рівня Turbo Pascal. Теоретичні відомості Якщо необхідно обчислити суму значень деякої функції y=f(x) при різних значення аргументу, то доцільно буде організувати цикл, в якому не тільки обчислюються поточні значення функції, але й накопичується їхня сума шляхом додавання одержаної суми до попередньої суми. Тому формула, що використовується для накопичення суми, має вигляд Аналогічно накопичується і добуток, тільки з тою різницею, що для його накопичення використовується формула |



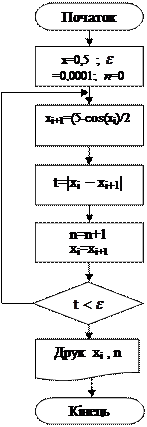
 -8.5=0
-8.5=0
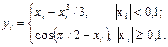




 ,
,  = 0,65 .
= 0,65 .














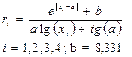







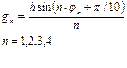









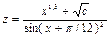


 . При першому виконанні циклу обчислюється значення
. При першому виконанні циклу обчислюється значення  , яке рівне
, яке рівне  . Тому початковому значенню суми перед циклом потрібно привласнити значення 0.
. Тому початковому значенню суми перед циклом потрібно привласнити значення 0. , а початковому значенню добутку привласнюється значення 1.
, а початковому значенню добутку привласнюється значення 1.