 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Послідовність виконання роботи 2 страница
Продовження таблиці 6.1
Продовження таблиці 6.1
ЛАБОРАТОРНА РОБОТА № 7 Тема: Turbo Pascal. Циклічні програми з регулярною зміною аргументу.
Мета: Формування умінь створення циклічних програм з регулярною зміною аргументу алгоритмічною мовою високого рівня Pascal.
Теоретичні відомості Цикл - це процес виконання деякого набору команд певну кількість разів. Розрізняють цикли, де кількість повторень відома заздалегідь, і цикли, де кількість повторень заздалегідь невідома, але її можна визначити під час виконання циклу. Тому цикли є: - з параметром , що реалізується оператором For і:=1 to n do <тіло циклу> . В цьому операторі задається кількість циклів від 1 до n. Параметр циклу іповинен бути тільки цілого типу. Такі цикли називаються циклами за лічильником; - з передумовою , що реалізується оператором While <умова> do <тіло циклу> ; - з післяумовою , що реалізується оператором Repeat <тіло циклу> Until <умова> . Тіло циклу являє собою послідовність операторів, які виконуються в циклі. Тіло циклу може складатись з одного оператора або послідовності операторів , обмежених операторними дужками begin… end. При складанні циклічної програм необхідно: - скласти графічний алгоритм, використавши оператор циклу або оператор циклу з передумовою чи післяумовою; - провести ідентифікацію змінних; - скласти програми з використанням оператора циклу і оператора з передумовою чи післяумовою; - розв’язати задачу на ЕОМ в діалоговому режимі; - провести аналіз результатів. Якщо за умовою задачі не заданий один з параметрів циклу (початкове, кінцеве значення параметра або крок зміни), то його необхідно визначити, користуючись залежністю
де N - кількість циклів; хп, хк - початкове і кінцеве значення параметра циклу;
Хід роботи 2.1 Постановка задачі
Скласти графічний алгоритм і програму обчислень таблиці значень функції
Значення сталої величини: a=8,9 . Аргумент Графічний алгоритм і програми скласти з використанням оператора циклу та оператора з передумовою чи після умовою.
2.2 Розв’язок задачі
Переведемо початкове значення аргументу та крок зміни аргументу з градусів в радіанну міру
Визначимо кінцеве значення аргументу
звідки
2.3 Графічний алгоритм
Графічний алгоритм з використанням оператора циклу з параметром показаний на рис. 7.1, з використанням оператора циклу з передумовою - на рис. 7.2.
2.4 Таблиця ідентифікації змінних
2.5 Програма мовою Pascal та результати обчислень
Program C1{цикли1}; Const a=8.6; Var y,a1:real; i:integer; Begin a1:=0.61; writeln('Результати обчислень: '); for i:=1 to 6 do begin y:=a*sqr(a1+pi/10)/(ln(a)-cos(a1/3)); writeln('a1=',a1:6:3,' y=',y:6:3); a1:=a1+0.87; еnd; end.
ні
так
Рисунок 7.1–Графічний алгоритм Рисунок 7.2–Графічний алгоритм
Результати обчислень: a1=0.610 y= 6.265 a1=1.480 y=21.781 a1=2.350 y=42.295 a1=3.220 y=64.146 a1=4.090 y=85.729 a1=4.960 y=107.073
Program C2{цикли2}; Const a=8.6; Var y,a1:real; Begin a1:=0.61; writeln('Результати обчислень: '); while a1<=4.96 do begin y:=a*sqr(a1+pi/10)/(ln(a)-cos(a1/3)); writeln('a1=',a1:6:3,' y=',y:6:3); a1:=a1+0.87; еnd; end. Результати обчислень: a1=0.610 y= 6.265 a1=1.480 y=21.781 a1=2.350 y=42.295 a1=3.220 y=64.146 a1=4.090 y=85.729 a1=4.960 y=107.073
3 Контрольні запитання 1. Які дані необхідні для організації циклу? 2. Що таке цикл? 3. В яких межах змінюється параметр циклу в наведених програмах? 4. Яка різниця в алгоритмах циклів, побудованих за допомогою оператора циклу і за допомогою умовних операторів? 5. Який оператор в наведених програмах контролює умову виходу з циклу? 6. Дайте зрівняльну характеристику програм з використанням оператора з передумовою і оператора циклу з параметром? 7. З яких етапів складається цикл? 8. Яка різниця між циклом з передумовою та циклом з післяумовою? Варіанти завдань наведені в таблиці 7.1 . Таблиця 7.1 –Варіанти завдань
Продовження таблиці 7.1
Продовження таблиці 7.1
ЛАБОРАТОРНА РОБОТА № 8 Тема: TurboPascal. Циклічні програми , які містять розгалуження.
Мета: Формування умінь створення циклічних програм, які містять розгалуження алгоритмічною мовою високого рівня Pascal.
Теоретичні відомості Цикл - це процес виконання певного набору команд певну кількість разів. Розрізняють цикли, де кількість повторень відома заздалегідь і цикли, де вона заздалегідь невідома, але її можна визначити під час виконання циклу. Для виконання поставленої задачі необхідно: - побудувати графічний алгоритм; - скласти програму з використанням операторів циклу та розгалуження; - вивести на друк результати виконання програми; - розв’язати задачу на ЕОМ в діалоговому режимі; - проаналізувати одержані результати.
Хід роботи 2.1 Постановка задачі
Обчислити різницю між максимальним і мінімальним значеннями функції:
Аргумент х змінюється від початкового значення 0,1 з кроком 0,32 до кінцевого значення 6,5.
2.2 Графічний алгоритм показаний на рис. 8.1
2.3 Таблиця ідентифікації змінних
2.4 Програма мовою Pascal та результати обчислень
Program C_R{цикли_розгалуження}; Const a=0.28; Var y,x,max,min,rizn:real; Begin x:=0.1; max:=cos(x-a)/sqrt(x); min:=cos(x-a)/sqrt(x); while x<=6.5 do begin y:=cos(x-a)/sqrt(x); if y>max then max:=y; if y<min then min:=y; x:=x+0.32; end; rizn:=max-min; writeln('Результати обчислень: '); writeln('max=',max:6:3,' min=',min:6:3); writeln('rizn=',rizn:6:3); end. Результати обчислень: max=3.111 min=-0.546 rizn=3.658
ні ні
так так
Рисунок 8.1 – Графічний алгоритм
3 Контрольні запитання 1. Які дані необхідні для організації циклу? 2. Що таке цикл? 3. Напишіть програму без застосування оператора циклу. 4. Чи може розгалуження не входити до тіла циклу? 5. Побудуйте програму з використанням оператора циклу з післяумовою. 6. Як побудувати програму мовою TurboPascal за допомогою оператора циклу з параметром?
Варіанти завдань наведені нище:
8.1. Обчислити значення функції
у набуває значення від 0 до 8 з кроком 0,15. 8.2. Обчислити значення функції
де q=0,1; 0,3; 1,1; 1,25; 1,9; 2,8. Величини 8.3. Знайти найменше значення функції і відповідне їй значення аргумента:
Аргумент змінюється від початкового значення 0,3 з кроком 0,25 до кінцевого значення 3,3 (радіан). 8.4. Вивести на друк тільки від’ємні значення і їх кількість: Аргумент х змінюється від початкового значення 1,1 з кроком 0,2 до кінцевого 4,1. 8.5. Знайти найменше додатнє і найменше від’ємне значення функції і відплвідне їм значення аргумента:
Аргумент х змінюється від початкового значення 0,1 з кроком 0,15 до кінцевого 3,1 (радіан). 8.6. Обчислити різницю між максимальним і мінімальним значеннями функції:
Аргумент х змінюється від початкового значення 0,1 зкроком 0,32 до кінцевого значення 6,5. 8.7. Знайти квадрат максимального значення функції:
Аргумент х змінюється від початкового значення 1/16 з кроком 0,25 до кінцевого 4,2. 8.8. Обчислити всі значення функції і аргумента:
Аргумент b змінюється від початкового значення 9,5 з кроком 0,25 до кінцевого 12,75. 8.9. Обчислити значення функції і вивести на друк окремо відємні, а окремо додатні значення функції і відповідні значення їм аргументів:
Аргумент х змінюється від початкового значення 1,2 з кроком 0,15 до кінцевого 4,4. 8.10. Вивести на друк значення функції, які задовольняють умову у<2,5 i y>1,5:
Аргумент а змінюється від початкового значення 1,15 до кінцевого 6,3. Кількість значень аргумента n=9. 8.11. Вивести на друк значення, які задовольняють умову у>1,35 i y<2,4, і відповідні значення аргумента. Аргумент х змінюється від 0,42 до 0,86 з кроком 0,04:
8.12. Обчислити добуток мінімального і максимального значень функції. Кількість значень аргумента n=19. Аргумент y змінюється від початкового значення 0,1 з кроком 0,75 (радіан):
8.13. Вивести на друк значення функції, які лежать в межах a>b>c, підрахувати їх кількість.
Аргумент х змінюється від початкового значення 3,4 з кроком 0,11 до кінцевого 6,6. 8.14. Обчислити 20 значень функції і відповідних значень аргумента, а також окремо вивести на друк максимальне зна-чення функції:
Аргумент с змінюється від початкового значення 1,35 до кінцевого 4,35 з постійним кроком. 8.15. Вивести на друк ті значення функції у і їх кількість, які лежать в межах 2,5>y>-1,5:
Аргумент с змінюється від початкового значення 4,2 до 8,3 з кроком 0,15. 8.16. Обчислити члени послідовності
які задовольняють умову 1,5<a<3,8; m=1,2,3,...,16. 8.17. Обчислити таблицю значень функції
для значень х, які змінюються від 0,5 до 8,5 включно з кроком 0,05. При цьому, якщо знаменник менше 10-3 за абсолютним значенням, то покласти у=106. Коефіцієнти а і b ввести з клавіатури. 8.18. Скласти блок-схему алгоритму і програму для розв’язу-вання квадратного рівняння
Якщо дискримінант додатній, то вивести на друк дійсні корені. Якщо дискримінант від’ємний, то вивести окремо дійсну і уявну частини коренів. Введення чисел a, b, q виконати з клавіатури. 8.19. За відомими декартовими координатами х і у довільної точки на площині визначити її полярні координати ρ і φ. При цьому
а полярний кут
8.20. Обчислити пари функцій f1 i f2, якщо межі зміни аргументів однакові. На друк вивести значення функції і аргумента.
Якщо аргумент лежить за вказаними межами, то вивести на друк значення аргумента і повідомлення “ФУНКЦІЯ НЕ ЗНАЙДЕНА”. Числові значення аргумента ввести з клавіатури. 8.21. Температуру з градусів за шкалою Цельсія (С) в градуси за шкалою Фаренгейта (F) переводять за залежністю
Перевести температури від 12ОС до 30ОС з кроком 1ОС. 8.22. Зміна потужності випромінювання ізотопів Q в чаС t описується залежністю
де Визначити, через скільки діб потужність випромінювання ізотопу, період піврозпаду якого дорівнює 8 діб, знизиться до безпечної величини 0,15 рентгена на годину, 8.23. Тиск рідини з глибиною зростає. Надрукувати таблицю зміни тиску глинистого розчину в середині через кожні 150 м. Глибина свердловини - 1800 м, густина розчину 8.24. За перший рік розробки нафтового родовища видобуток нафти склав 200 тис. т на рік. В наступні роки видобуток нафти зростав на 8% за рік. Визначити, скільки буде видобуто нафти з родовища за 25 років. 8.25. Для умови задачі 4,24 обчислити, через який найменший строк видобуток нафти складатиме не менше 350 тис. т нафти за рік.
ЛАБОРАТОРНА РОБОТА № 9 Тема: TurboPascal. Ітераційні циклічні програми.
Мета: Формування умінь складання програм для розв’язування рівнянь методом ітерації алгоритмічною мовою високого рівня Pascal.
Теоретичні відомості Особливістю ітераційних циклів є те, що наперед невідома кількість циклів, які виконуються. Обчислення в циклі припиняється при досягненні заданої точності. Ітераційні цикли будуються за допомогою операторів умовного і безумовного переходів, а також використовуються структури організації циклів з передумовою чи з післяумовою. Для заданого рівняння необхідно: - скласти графічний алгоритм для визначення кореня рівняння із заданою похибкою методом ітерацій. В алгоритмі передбачити лічильник кількості ітерацій; - скласти програму для ЕОМ; - розв’язати рівняння на ЕОМ в діалоговому режимі; - провести аналіз одержаного результату. Хід роботи 2.1 Постановка задачі
Знайти корінь рівняння cos(x)+2x-5=0 на інтервалі [0;1] з точністю
2.2 Розв’язок задачі |
,
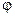
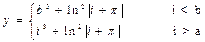
- крок зміни параметра циклу.
.
змінюється від початкового значення 350 з постійним кроком 500, кількість інтервалів параметра n=6.
; 
.
,
,
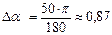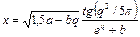
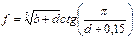
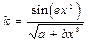
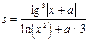
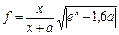
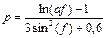
=2; 2,4; 2,8; 3,2; 3,6; 4,0;
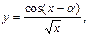
b = 4,85.
.
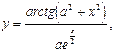
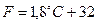- початкова потужність;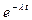 
- період піврозпаду.
рентгена на годину.
=1300 кг/м.
=0,0001, користуючись методом ітерацій.