 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Характеристики випадкового процесу 12
1. Математичне сподівання випадкового процесу у момент tk : для дискретних випадкових величин
Для безперервних випадкових величин
Точкова оцінка математичного сподівання
2. Дисперсія випадкового процесу у момент tk :
де i- номер реалізації випадкового процесу Для безперервних випадкових величин
3. Середнє - квадратичне відхилення випадкового процесу у момент tk :
4. Кореляційна функція 2-ох випадкових процесів – відображає зв’язок (залежність) значень випадкового процесу x(ti) та значень випадкового процесу y(ti) один від одного.
5. Aвтокореляційна функція випадкового процесу відображає зв’язок (залежність) значень одного випадкового процесу x(t) в різні моменти часу ti та ti+k ( відстань у часі k має назву лаг) один від одного.
1.4.2.Алгоритм аналізу часових рядів [2] Звичайно при аналізі часових рядів послідовно проходять наступні етапи (блок-схема алгоритму представлена на рис.4.1). Крок 1. Вводимо часовий ряд з передісторією за декілька років. Крок 2. Розраховуємо тренд (коефіцієнти тренду b0, b1, b2). Визначаємо коефіцієнти тренду b0, b1, b2, мінімізуючи функцію суми квадратів похибок для всіх спостережень :
де yi - значення часового ряду, t- час.
В цьому випадку градієнт мінімізуємої функції
де Використовуємо метод найшвидшого спуску, перераховуючи коефіцієнти наступними формулами
Крок 3. Обраховуємо тренд відповідно від кількості коефіцієнтів (квадратичний):
Крок 4. Перевірка коефіцієнтів b0, b1, b2 на значимість критерієм Ст'юдента:
де
Якщо Розраховане значення критерію Ст’юдента порівнюють з його табличним значенням з обраним рівнем довіри (як правило, 0.95) і числі ступенів свободи N-k-1, де N – кількість точок, k – кількість змінних в регресійному рівнянні. Якщо абсолютне значення Крок 5. Перевірка моделі на адекватність виконується за критерієм Фішера:
Розраховане значення критерію Фішера порівнюють з табличним значенням квантилю Фішера для обраного рівня довіри (як правило, 0.95) та ступенів вільності k-1 і N-k. Якщо обчислене значення F>F Крок 6. Обчислення сезонної та випадкової компонент. Спочатку вилучаємо з процесу тренд та сезонну складову. Потім, якщо є щомісячні спостереження протягом декількох років, обчислюємо середньо сезонну компоненту і випадкову компоненту Мультиплікативна модель:
де Т – період (Т = 12 місяців); (М+1) – число років спостережень; i = 1 .. N. Випадкова компонента:
Адитивна модель:
де Т – період (Т = 12 місяців); (М+1) – число років спостережень; i = 1.. N. Випадкова компонента:
Якщо нема щомісячних спостережень протягом декількох років Крок 7. Побудова автокореляційної функції випадкової компоненти залишків та перевірка правильності тренд - аналізу: для адитивної моделі:
де k – зсув по часу (k = 0 .. 15, k < N). для мультиплікативної моделі:
де k – зсув по часу (k = 0 .. 15, k < N).
Тренд-аналіз виконаний вірно, якщо автокореляційна функція випадкової компоненти згасає. На рис. 1.4.1 зображено блок-схему алгоритму тренд-аналізу. Дуже далеко рис.
12 |



 , де i- номер реалізації випадкового процесу
, де i- номер реалізації випадкового процесу  (1.4.3)
(1.4.3) - ймовірність того, що випадкова величина прийме значенняXi у момент tk
- ймовірність того, що випадкова величина прийме значенняXi у момент tk ,де (1.4.4)
,де (1.4.4) -- густина розподілу ймовірності випадкового процесу
-- густина розподілу ймовірності випадкового процесу , де i- номер реалізації випадкового процесу .
, де i- номер реалізації випадкового процесу .  , (1.4.6)
, (1.4.6) (1.4.7)
(1.4.7) (1.4.8)
(1.4.8) (1.4.9)
(1.4.9) (1.4.10)
(1.4.10) (1.4.11)
(1.4.11) <0.001,
<0.001, (1.4.12)
(1.4.12) (1.4.13)
(1.4.13)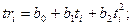 i = 1 .. N.
i = 1 .. N. , і = 1, 2. , (1.4.14)
, і = 1, 2. , (1.4.14) 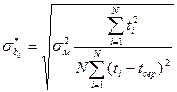
 ,
,  ;
; , то коефіцієнт не значимий, інакше коефіцієнт значимий.
, то коефіцієнт не значимий, інакше коефіцієнт значимий. вище, ніж табличне, то коефіцієнт регресії є значущим з даним рівнем довіри. В іншому випадку є підстави для виключення відповідної змінної з регресійної моделі.
вище, ніж табличне, то коефіцієнт регресії є значущим з даним рівнем довіри. В іншому випадку є підстави для виключення відповідної змінної з регресійної моделі. . (1.4.15)
. (1.4.15) , то побудована модель адекватна, в іншому випадку модель вважається неадекватною.
, то побудована модель адекватна, в іншому випадку модель вважається неадекватною. ; i = 1 .. N; (3.11)
; i = 1 .. N; (3.11) , (4.16)
, (4.16) ; i = 1 .. N. (1.4.17)
; i = 1 .. N. (1.4.17) ; i = 1 .. N; (1.4.18)
; i = 1 .. N; (1.4.18) 

 , (1.4.19)
, (1.4.19) , - дисперсія випадкової компоненти
, - дисперсія випадкової компоненти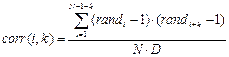 , (1.4.20)
, (1.4.20) , - дисперсія випадкової компоненти
, - дисперсія випадкової компоненти