 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Часовий ряд та його компоненти 12
Складові випадкового процесу Тренд (математичне сподівання середня лінія процесу) Сезона складова Випадкова складова Циклічна складова Правильність тренд – аналізу обчислюється по авто кореляційної функції випадкової складової Випадкова компонента обчислюється таким виглядом : для адитивної моделі для мультиплікативної моделі
Після цього перевіряють чи являється Xв(t) стаціонарним процесом і якщо Xв(t) – стаціонарний процес, то по виду автокореляційної функції Xв(t) визначають іі модель.
Aвтокореляційна функція випадкової компоненти відображає залежність значення випадкової компоненти Xв(ti) від значення тієї ж випадкової величини Xв(ti+k), де k – відстань у часі:
Оцінка автокореляційної функції
Стаціонарні випадкові процеси - випадкові процеси,в яких математичне сподівання та дисперсія постійні протягом часу, а авто кореляційна функція Якщо при k Якщо при тренд-аналізі випадкового процесу правильно визначено тренд і вилучено з процесу , а також визначена і видалена сезонна компонента то автокореляційна функція випадкової компоненти(RANDOM) Якщо при тренд-аналізі випадкового процесу не правильно визначено тренд, або не вилучено з процесу, то Якщо при тренд-аналізі випадкового процесу не правильно визначена або вилучена сезонна компонента то c
По вигляду автокореляційної функції можна визначити такі моделі випадкової компоненти випадкового процесу: Рис. 13. Модель:
Рис. 14. Модель:
Рис. 15. Модель:
Далі, маючи модель випадкового процесу і моделі усіх складових випадкового процесу можна спрогнозувати випадковий процес для майбутніх значень t для детермінованного тренду Довгострокове прогнозування часових рядів Стислі теоретичні відомості Часовий ряд та його компоненти Однією з базових концепцій кількісних методів прогнозування є декомпозиція часового ряду. Згідно цій концепції часовий ряд може бути проаналізований і прогнозований з точки зору окремих його компонент, кожна з яких може бути розрахована окремо. Традиційно виділяють чотири основні компоненти часового ряду: тренд, циклічну компоненту, сезонну компоненту і нерегулярну (випадкову) компоненту. Тренд. Трендом часового ряду Розрізняють процеси з детермінованим трендом та стохастичним трендом. Детермінований тренд – тренд, який не містить випадкову компоненту і коефіцієнти, якого не змінюються протягом довготривалого проміжку у часі. Стохастичний тренд – тренд, який так, як і процес, містить випадкову компоненту і коефіцієнти якого швидко змінюються у часі. Сезонна компонента. Сезонна компонента часового ряду Головна ідея підходу до аналізу сезонних компонент полягає в переході від порівняння всіх значень часового ряду між собою до порівняння значень через певний період часу. Це дозволяє значно знизити оцінку варіації часового ряду коло свого середнього значення. Циклічна компонентачастіше зустрічається у випадкових процесах, що описують технічні характеристики.Якщо тренд – це плавні зміни, що з’являються на великих часових проміжках, якщо сезонна компонента – це періодична функція часу, чітко видима, коли її період набагато менше загального часу спостереження, то під циклічною компонентою звичайно розуміють зміни часового ряду, достатньо плавні і помітні для того, щоб не включати їх у випадкову складову, але такі, які не можна віднести ні до тренду, ні до періодичної складової. Циклічна компонента може бути представлена як сума гармонік ряду. Нерегулярна або випадкова компонента et – складається з непередбачуваних або випадкових коливань. Відповідно до класичної моделі, ці нерегулярні сили є занадто непередбачуваними для прогнозування. Моделі тренду Розрізняють наступні моделі тренду: 1. проста лінійна модель: 2. поліноміальна модель: 3. експоненціальна модель: 4. логістична модель: 5. модель Гомперця: Дві останні моделі задають криві тренда S-подібної форми. Вони відповідають процесам з постійно зростаючими темпами росту в початковій стадії і постійно затухаючими темпами росту в кінці. Необхідність подібних моделей зумовлена неможливістю багатьох економічних процесів довгий час розвиватися з постійними темпами росту чи за поліноміальними моделями у зв’язку з їх доволі швидким зростанням (чи зменшенням). Перше уявлення про можливий характер тренду дає графічне представлення часового ряду. При прогнозуванні тренд використовують в першу чергу для довгострокових прогнозів. Точність короткострокових прогнозів, заснованих тільки на підібраній кривій тренду, як правило, недостатня. Існує два основні підходи до математичного опису взаємозв’язку складових: - адитивний, коли кожна поточна величина часового ряду розглядається як сума цих компонент; - мультиплікативний, коли кожна поточна величина часового ряду розглядається як добуток цих компонент. Відповідно дві моделі процесу: - адитивна модель:
- мультиплікативна модель:
Модель часового ряду можливо визначити по графіку. Якщо модель адитивна, то розмахи коливань (різниці між найближчими максимумами та мінімумами) не змінюються при відповідної зміни тренду. Якщо модель мультиплікативна, то розмахи коливань (різниці між найближчими максимумами та мінімумами) змінюються при відповідної зміни тренду. 12 |





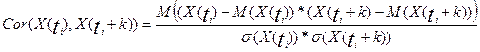 .
.
 залежить від відстані у часі k, а не від того, де розташовано t.
залежить від відстані у часі k, а не від того, де розташовано t.


 то стаціонарний процес набуває ергодичну властивість і статистику можно набирати не по різним реалізаціям процесу, а по одній реалізації, яка достатньо довго триває у часі і яку можливо розглядати як декілька різних реалізацій процесу
то стаціонарний процес набуває ергодичну властивість і статистику можно набирати не по різним реалізаціям процесу, а по одній реалізації, яка достатньо довго триває у часі і яку можливо розглядати як декілька різних реалізацій процесу при k
при k  не згасає при k
не згасає при k 



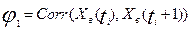





 називають математичне сподівання, (середню лінію на графіку) нециклічну компоненту, що описує вплив довгострокових факторів.
називають математичне сподівання, (середню лінію на графіку) нециклічну компоненту, що описує вплив довгострокових факторів. описує поведінку, що змінюється регулярно впродовж заданого періоду (року, місяця, тижня, дня і т.п.). Вона складається з послідовності майже повторюваних циклів.
описує поведінку, що змінюється регулярно впродовж заданого періоду (року, місяця, тижня, дня і т.п.). Вона складається з послідовності майже повторюваних циклів. ;
; , де значення степені полінома n в практичних задачах рідко перевищує 5;
, де значення степені полінома n в практичних задачах рідко перевищує 5; . Ця модель частіше за все застосовується для даних, що мають тенденцію зберігати постійні темпи приросту;
. Ця модель частіше за все застосовується для даних, що мають тенденцію зберігати постійні темпи приросту; ;
; , де 0 < r <1.
, де 0 < r <1. , (1.4.1)
, (1.4.1) . (1.4.2)
. (1.4.2)