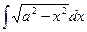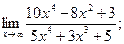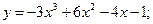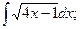ПОЗНАВАТЕЛЬНОЕ

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Раздел 3. ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ.

Тема 3.1. Вероятность. Теоремы сложения и умножения вероятностей.

Понятие события и вероятности события. Достоверные и невозможные события. Классическое определение вероятностей. Теорема сложения вероятностей. Теорема умножения вероятностей.

Студент должен знать:

- понятия: событие, частота и вероятность, совместные и несовместные события.

- теорема сложения вероятностей;

- теорема умножения вероятностей;

Студент должен уметь:

-находить вероятность в простейших задачах;

Тема 3.2. Случайная величина, ее функция распределения.

Случайная величина. Дискретная и непрерывная случайные величины. Закон распределения случайной величины.

Студент должен знать:

- способы задания случайной величины;

- определение непрерывной и дискретной случайных величин;

- закон распределения случайной величины;

Тема 3.3. Математическое ожидание и дисперсия случайной величины.

Математическое ожидание дискретной случайной величины. Дисперсия случайной величины. Среднее квадратичное отклонение случайной величины.

Студент должен знать:

- определение математического ожидания, дисперсии дискретной случайной величины;

- среднее квадратичное отклонение;

Студент должен уметь:

- находить математическое ожидание и дисперсию случайной величины по закону;

- находить среднее квадратичное отклонение случайной величины;

Раздел 4. ОСНОВНЫЕ ЧИСЛЕННЫЕ МЕТОДЫ.

Тема 4.1. Численное интегрирование.

Формулы прямоугольников. Формула трапеций. Формула Симпсона. Абсолютная погрешность при численном интегрировании.

Студент должен знать:

- способы представления функции в виде прямоугольников и трапеций;

-формулу Симпсона;

Студент должен уметь:

- вычислять интеграла по данным формулам;

Тема 4.2. Численное дифференцирование.

Численное дифференцирование. Формулы приближенного дифференцирования. Погрешность в определении производной.

Студент должен знать:

- интерполяционные формулы Ньютона;

- таблицу конечных разностей;

Студент должен уметь:

- по табличным данным находить аналитическое выражение производной;

1.Контрольная работа составлена в пяти вариантах.

Варианты работы студенты определяют по начальной букве своей фамилии.

2. Работа выполняется в ученической тетради, синими чернилами разборчивым почерком , без сокращений с соблюдением интервалов между строк и полями для замечаний преподавателя. Контрольная работа должна быть выполнена в установленный срок, срок нахождения контрольной работы в ОУ для проверки составляет 10 дней, после чего студент забирает контрольную работу на доработку или получает рецензию с отметкой, в учебной части ОУ.

3. На титульном листе указать фамилию, имя, отчество слушателя, его адрес с указанием почтового индекса, номер зачетной книжки, номер контрольной работы и вариант, конверт с адресом для отправки.

4. Если контрольная работа выполнена с нарушением данных указаний или не полностью, она возвращается слушателю без проверки.

5. Если работа не зачтена, ознакомьтесь с рецензией на работу и изучите ошибки. Работу следует переделать в соответствии с рекомендациями рецензента.

6. Переделанную работу предоставить на проверку вместе с не зачтенной работой, в срок, который указан в рецензии.

7. В конце работы должен быть приведён список использованной литературы с указанием автора, названия, места и года издания.

Вариант	Буква фамилии
	от А до Е
	от Ё до И
	от К до О
	от П до У
	от Ф до Я

Вариант I

1) Найти пределы функций

2) Найти производные функций

3) Найти неопределенный интеграл функций

4) Определить площадь фигуры, заключенной между ветвью кривой у = х², осью Ох и прямыми х = 0, х = 3.

5) Решить дифференциальное уравнение

6) Решить задачу:

Номер серии выигрышного билета вещевой лотереи состоит из пяти цифр. Определить вероятность того, что номер первой выигравшей серии будет состоять из одних нечетных цифр.

7) С помощью таблицы распределения случайной величины найти:

а) математическое ожидание;

б) дисперсию;

в) среднее квадратичное отклонение.

х
р

Вариант II

1) Найти пределы функций

2) Найти производные функций

3) Найти неопределенный интеграл функций

4) Найти площадь фигуры, заключенной между осью Ох и кривой у = х²-4х.

5) Решить дифференциальное уравнение

6) Решить задачу:

В сосуде находится 11 шаров, из которых 4 цветных и 7 белых. Найти вероятность двукратного извлечения из сосуда цветного шара: а) если вынутый шар возвращается обратно в сосуд и б) если вынутый шар в сосуд не возвращается.

7) С помощью таблицы распределения случайной величины найти:

а) математическое ожидание;

б) дисперсию;

в) среднее квадратичное отклонение.

х
р

Вариант III

1) Найти пределы функций

2) Найти производные функций

3) Найти неопределенный интеграл функций

4) Найти площадь фигуры, заключенной между у = х³, х = -1, х = 2 и осью Ох.

5) Решить дифференциальное уравнение

6) Решить задачу:

В мешке смешаны нити трех цветов: белых – 50%, красных – 30%, черных – 20%. Определить вероятность того, что при последовательном вытягивании наугад трех нитей окажется: а) все нити – одного цвета; б) все нити разных цветов.

7) С помощью таблицы распределения случайной величины найти:

а) математическое ожидание;

б) дисперсию;

в) среднее квадратичное отклонение.

х
р

Вариант IV

1) Найти пределы функций

2) Найти производные функций

3) Найти неопределенный интеграл функций

4) Найти площадь фигуры, ограниченной линиями xу = - 6, у - х = 7

5) Решить дифференциальное уравнение

6) Решить задачу:

Вероятность выигрыша по лотерейному билету равна 0,15. Какова вероятность того, что, по крайней мере, один из четырех билетов выиграет?

7) С помощью таблицы распределения случайной величины найти:

а) математическое ожидание;

б) дисперсию;

в) среднее квадратичное отклонение.

х
р	0,3	0,4	0,1	0,1	0,05	0,05

Вариант V

1) Найти пределы функций

2) Найти производные функций

3) Найти неопределенный интеграл функций

4) Найти площадь фигуры, ограниченной линиями у = e^x, у = 0, x=-1 ,x=1

5) Решить дифференциальное уравнение

y`=10^x⁺^y

6) Решить задачу:

В партии из 100 одинаковых по наружному виду изделий смешаны 40 штук I сорта и 60 штук II сорта. Найти вероятность того, что взятые наудачу два изделия окажутся: а) одного сорта; б) разных сортов.

7) С помощью таблицы распределения случайной величины найти:

а) математическое ожидание;

б) дисперсию;

в) среднее квадратичное отклонение.

х
р	0,3	0,2	0,1	0,25	0,75	0,3

Вопросы к зачету

1. первый и второй замечательные пределы;

2. определение производной;

3. формулы производных суммы, произведения и частного;

4. основные методы интегрирования;

5. формула Ньютона-Лейбница;

6. свойства интегралов;

7. определение дифференциального уравнения;

8. определение общего и частного решений дифференциальных уравнений;

9. методы решения дифференциальных уравнений;

10. определение числовых и функциональных рядов;

11. признаки сходимости;

12. определение множества и отношения;

13. операции и свойства операций над множествами;

14. свойства отношений;

15. определение графов и его элементов;

16. виды графов и операции над ними;

17. понятия: событие, частота и вероятность, совместные и несовместные события.

18. теорема сложения вероятностей;

19. теорема умножения вероятностей;

20. способы задания случайной величины;

21. определение непрерывной и дискретной случайных величин;

22. закон распределения случайной величины;

23. определение математического ожидания, дисперсии дискретной случайной величины;

24. среднее квадратичное отклонение;

25. способы представления функции в виде прямоугольников и трапеций;

26. формула Симпсона;

27. интерполяционные формулы Ньютона;

28. таблица конечных разностей;

Литература

1. Филимонова Е.В. Математика : Учебное пособие для средних специальных учебных заведений, 2004- 416с.

2. Ермакова В.И. Справочник по математике для экономистов, 1987-336с.

3. Лапчик М.П. Численные методы.

4. Баврик И.И. Высшая математика.

5. Власов В.Г. Конспект лекций по высшей математике.

6. Данко П.Е. Высшая математика в упражнениях и задачах.

7. Щипачев В.С. Основы высшей математики.