 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Мішаний добуток трьох векторів. 12
Якщо векторний добуток двох векторів
Мішаний добуток має просте геометричне тлумачення – це скаляр, який за абсолютною величиною дорівнює об’єму паралелепіпеда, побудованого на даних трьох векторах. Якщо вектори Мішаний добуток трьох векторів дорівнює нулеві тоді, коли ці вектори компланарні, тобто умова компланарностітрьох векторів має вигляд:
Мішаний добуток не змінюється, якщо має місце переставлення співмножників за колом і змінює знак, якщо в такому переставленні порушено послідовність співмножників:
Тому мішаний добуток векторів
Помітимо, що якщо в мішаному добутку є два колінеарні вектори, то він дорівнює нулеві. Приклад 1. Три вершини тетраедра знаходяться в точках А(2; 1; -1), В(3; 0; 1), С(2; -1; 3). Знайти координати четвертої вершини D, яка належить вісі Оу, якщо об’єм тетраедра дорівнює 3 куб. од.
Розв’язання: Оскільки точка D належить вісі Оу, то її координати
Розв’язуючи це рівняння, дістанемо, що Приклад 3. Довести, що чотири точки Розв’язання: Для того, щоб довести, що чотири точки лежать в одній площині, достатньо довести, що три вектора, початком яких є деяка з даних чотирьох точок, а кінцями є інші три точки, лежать в одній площині, тобто, що ці три вектори компланарні. За спільний початок векторів виберемо точку А, тоді:
Вектори
Отже, одержали, що вектори Приклад 4. Задана піраміда з вершинами в точках А(1; 2; 3), В(‑2; 4; 1), С(7; 6; 3), D(4; ‑3; ‑1). Знайти: а) довжину ребер б) площу грані АВС; в) кут між ребрами г) об’єм піраміди; д) довжину висоти, опущеної на грань АВС. Розв’язання: а) Знайдемо вектори
Знайдемо модулі цих векторів:
б) Площа грані АВС буде дорівнювати:
в) Кут між ребрами
г) Об’єм піраміди обчислимо за формулою:
д) Довжину висоти h, опущеної на грань АВС, можна знайти, користуючись формулою:
Таким чином .
ЩО ПОВИНЕН ЗНАТИ СТУДЕНТ 1. Поняття вектора. 2. Поняття одиничного і нульового вектора. 3. Модуль вектора, формула відстані між двома точками. 4. Поняття колінеарності векторів. 5. Лінійні операції над векторами. 6. Поняття проекції вектора на вісь. 7. Скалярний добуток векторів
КОНТРОЛЬНЫЙ ТЕСТ 1. На каком рисунке изображён вектор a) 2. Два вектора называются коллинеарными, если: a) они лежат в одной плоскости; б) они лежат в параллельных плоскостях; в) они лежат на параллельных прямых; г) они не лежат на параллельных прямых. 3. Укажите координату a) 1; б) 2; в) 4. Какая формула задаёт длину вектора a) 5. Найдите длину диагонали a) 6. Составьте вектор a) 7. Скалярным произведением векторов a) число 8. Найдите скалярное произведение векторов a) -12; б) 20; в) -10; г) 18. 9. Какими являются векторы a) ортогональными; б) коллинеарными; в) компланарными; г) равными. 10. Какие среди векторов a)
12 |



 помножити скалярно на третій вектор
помножити скалярно на третій вектор  , то такий добуток трьох векторів називається мішаним (векторно-скалярним) і позначається так:
, то такий добуток трьох векторів називається мішаним (векторно-скалярним) і позначається так: =
= 
 ,
,  ,
, 

 (49).
(49). (0; у; 0). Об’єм тетраедра ABCD можна розглядати як
(0; у; 0). Об’єм тетраедра ABCD можна розглядати як 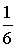 об’єму паралелепіпеда, побудованого на векторах
об’єму паралелепіпеда, побудованого на векторах  як на ребрах:
як на ребрах:
 .
. отже
отже  .
. лежать в одній площині.
лежать в одній площині.
 будуть компланарними тоді, коли їх мішаний добуток дорівнює нулеві.
будуть компланарними тоді, коли їх мішаний добуток дорівнює нулеві.
 = ‑2+12‑8‑2=0.
= ‑2+12‑8‑2=0. і
і  ;
;




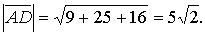




 звідки
звідки 

 :
: ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. вектора
вектора  , изображённого на рисунке
, изображённого на рисунке 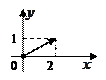
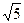 ; г) -1.
; г) -1. :
: ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. четырёхугольника
четырёхугольника  , если
, если  ,
,  ,
,  ,
,  :
: ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. , если
, если  ,
,  .
.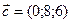 ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. называется:
называется: , где
, где  и
и  — длины векторов; б) число
— длины векторов; б) число 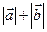 , где
, где  ; г) число
; г) число  , где
, где  — угол между векторами.
— угол между векторами. и
и  , если
, если  ,
, 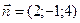 .
. и
и  , если
, если  ,
,  ,
,  ,
,  :
: ,
,  ,
,  ,
,  ортогональны:
ортогональны: ; б)
; б)  ; г)
; г)