Властивості скалярного добутку. ЛЕКЦІЯ 3. ВЕКТОРНА АЛГЕБРА План 1. Вектори. Операції над ними. Декартові прямокутні координати вектора. Довжина вектора. Скалярний добуток векторів. Векторний добуток двох Мішаний добуток трьох векторів. Вектори. Операції над ними. Вектором називається спрямований відрізок. Вектор з початком в точці  і кінцем у точці і кінцем у точці  позначається символом позначається символом  (або однією буквою (або однією буквою  , ,  , ...). , ...). Модулем (довжиною) вектора  називається довжина відрізка називається довжина відрізка  і позначається, і позначається,  , ,  . . Одиничним називається вектор, довжина якого дорівнює одиниці. Одиничний вектор позначають  . . Нульовим називається вектор, довжина якого дорівнює нулю. Нульовий вектор позначається  . . Колінеарними називаються вектори  і і  , якщо вони лежать на одній прямій або на паралельних прямих; записують , якщо вони лежать на одній прямій або на паралельних прямих; записують  . . Компланарними називаються три (і більше) вектора, якщо вони лежать в одній площині або в паралельних площинах. Рівними називаються два колінеарних вектори  и и  ( (  ), якщо вони однаково спрямовані і мають рівні довжини. ), якщо вони однаково спрямовані і мають рівні довжини. Додавання векторів. Сумою двох векторів  і і  називається вектор називається вектор  , що з'єднує початок вектора , що з'єднує початок вектора  з кінцем вектора з кінцем вектора  , відкладеного від кінця вектора , відкладеного від кінця вектора  . . . 
Добуток вектора на число. Добутком вектора  на число на число  називається вектор, який має довжину називається вектор, який має довжину  і який має напрям вектора і який має напрям вектора  в разі в разі  та протилежний напрямок у разі та протилежний напрямок у разі  . . Приклад .1. Дано вектори  і і  . Побудуйте вектори: 1) 1) . Побудуйте вектори: 1) 1)  ; 2) ; 2)  . . 

Декартові прямокутні координати вектора. Довжина вектора. Нехай вектор  складає кут складає кут  з віссю з віссю  . . Проекцією вектора  на вісь на вісь  називається число, рівне довжині вектора називається число, рівне довжині вектора  (рис.1), взятої зі знаком «плюс», якщо напрям вектора (рис.1), взятої зі знаком «плюс», якщо напрям вектора  збігається з напрямком осі і зі знаком «мінус» у противному випадку. збігається з напрямком осі і зі знаком «мінус» у противному випадку. Проекцію вектора  на вісь на вісь  можна обчислити за формулою: можна обчислити за формулою:  . .

Декартовими прямокутними координатами  вектора вектора  називаються його проекції на відповідні координатні осі називаються його проекції на відповідні координатні осі  . . Вектор  з координатами з координатами  записують у вигляді записують у вигляді  або, або,  де де  - одиничні вектори координатних осей - одиничні вектори координатних осей  відповідно. Довжина вектора відповідно. Довжина вектора  визначається за формулою: визначається за формулою:  . .
Якщо вектор  заданий точками заданий точками  і і  , то його координати обчислюються за формулами: , то його координати обчислюються за формулами:  . .
Приклад 2. Дано дві точки  і і 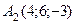 . Знайдіть координати і довжину вектора . Знайдіть координати і довжину вектора  . . За умовою задачі,  , ,  , ,  , ,  , ,  , ,  . Значить, . Значить,  . .  . .
Приклад 3. Дано два вектори  и и  . Знайдіть координати і довжину вектора . Знайдіть координати і довжину вектора  . .  ; ;  ; ;
 ; ;
 . .
Поєднаємо паралельним переносом початок деякого вектора  з початком координат прямокутної системи координат з початком координат прямокутної системи координат  . Нехай . Нехай  - кути, які утворює вектор - кути, які утворює вектор 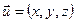 з осями координат з осями координат  відповідно (рис.2). Напрям вектора відповідно (рис.2). Напрям вектора  визначається за допомогою направляючих косинусів визначається за допомогою направляючих косинусів  , ,  , ,  , для яких справедливі рівності: , для яких справедливі рівності: Скалярний добуток векторів. Скалярним добутком двох ненульових векторів  і і  називається число, рівне добутку довжин цих векторів на косинус кута називається число, рівне добутку довжин цих векторів на косинус кута  між ними (див. рис.3): між ними (див. рис.3): 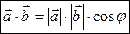 . .
З рис. 3 видно, що  . . Тому  або або  . (*) . (*) Властивості скалярного добутку. 1.  — переставний (комутативний) закон. — переставний (комутативний) закон. 2.  — розподільний закон. — розподільний закон. 3. Якщо  то то  . . 4.   (або (або  чи чи 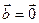 ). ). Зокрема, скалярний добуток одиничних векторів (ортів) задовольняє рівностям: 

1. Якщо вектори задані координатами  , ,  або або  , ,  , то , то  . .
2. Кут між векторами  і і  визначається за формулою: визначається за формулою:  . . 
3. Вектори  і і  колінеарні тоді і тільки тоді, коли їхні відповідні координати пропорційні, тобто: колінеарні тоді і тільки тоді, коли їхні відповідні координати пропорційні, тобто:  . .
4. Умова перпендикулярності векторів  и и  : :  . .
Приклад 4. Вектори  і і  утворюють кут утворюють кут  . Знаючи, що . Знаючи, що  и и  , обчисліть , обчисліть  . . 

 . .
 Приклад 5. Дано вершини трикутника Приклад 5. Дано вершини трикутника  , ,  и и  .Знайдіть: 1) внутрішній кут при вершині .Знайдіть: 1) внутрішній кут при вершині 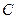 ; ;
2) 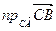 . . Для знаходження кута 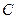 знайдемо вектори знайдемо вектори 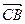 и и  . .  ; ;
 . .
Тоді    Т.е. Т.е.  Відповідно доформули (*)  . .
Векторний добуток двох Поряд із множенням двох векторів, яке приводить до скаляра, розглянемо ще один тип множення векторів, внаслідок якого дістаємо вектор. Таке множення називається векторним. Векторним добутком двох векторів  і і  називається вектор називається вектор  , який задовольняє таким умовам: , який задовольняє таким умовам: 1) Довжина вектора  дорівнює площі паралелограма, побудованого на векторах дорівнює площі паралелограма, побудованого на векторах  і і  , тобто , тобто  (37). (37).
2) Вектор  перпендикулярний до площини цього паралелограма, тобто перпендикулярний і до вектора перпендикулярний до площини цього паралелограма, тобто перпендикулярний і до вектора  , і до вектора , і до вектора  : :  та та  (38). (38).
3) Вектори  , ,  , ,  , взяті у такому порядку, утворюють праву трійку векторів. Упорядкована трійка некомпланарних векторів називається правою, якщо з кінця третього вектора найкоротший поворот від першого вектора до другого здійснюється проти обертання годинникової стрілки. , взяті у такому порядку, утворюють праву трійку векторів. Упорядкована трійка некомпланарних векторів називається правою, якщо з кінця третього вектора найкоротший поворот від першого вектора до другого здійснюється проти обертання годинникової стрілки. Для векторного добутку  вектора вектора  на вектор на вектор  вводиться позначення: вводиться позначення:  або або  (39). (39).
Якщо вектори-множники взаємно перпендикулярні, то модуль векторного добутку дорівнює добутку модулів співмножників:  якщо якщо  (40). (40).
Якщо вектори-множники колінеарні, то  і векторний добуток їх дорівнює нуль-вектору, тобто і векторний добуток їх дорівнює нуль-вектору, тобто  (41). (41).
Закон комутативності для векторного добутку  не виконується, або точніше вектор не виконується, або точніше вектор  має напрям, протилежний до має напрям, протилежний до  : :  (42). (42).
Властивість сполучності відносно скалярного множника зберігається:  (43). (43).
Властивість розподільності для векторного добутку також зберігається:  (44). (44).
Якщо векторний добуток двох векторів записати у координатній формі, то маємо:  (45). (45).
Приклад 1. Дано:   і і 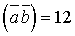 . Обчислити . Обчислити  . . Розв’язання: Відомо, що   . Для того, щоб розв’язати задачу, нам потрібно знайти . Для того, щоб розв’язати задачу, нам потрібно знайти  . З умови . З умови  маємо: маємо:  , звідки , звідки  = = 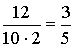 . Оскільки . Оскільки  >0, то >0, то  . . З тригонометричної тотожності знаходимо  : :  = = 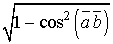 = =  . . Отже,   = =  . . Приклад 2. Трикутник задано вершинами А(1; ‑1; 2), В(5; ‑6; 2), С(1; 3; ‑1). Обчислити довжину висоти, опущеної з вершини В на сторону АС. Розв’язання: Знаходимо вектори 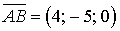 та та 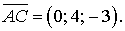 Тоді згідно з формулою Тоді згідно з формулою  та формулою (45) дістанемо: та формулою (45) дістанемо: 
Крім того,  , тобто , тобто  Отже, знаходимо Отже, знаходимо  і маємо і маємо  Приклад 3. Якій умові повинні задовольняти вектори  і і  , щоб вектори , щоб вектори  та та  були колінеарними? були колінеарними? Розв’язання: Щоб ненульові вектори  та та  були колінеарні, необхідно, щоб модуль їх векторного добутку дорівнював нулеві, тобто були колінеарні, необхідно, щоб модуль їх векторного добутку дорівнював нулеві, тобто 
 , ,

Але  і і  , отже , отже  звідки звідки  або або  , тобто вектори , тобто вектори  і і  повинні бути колінеарними. повинні бути колінеарними. Приклад 4. Вектори  , ,  і і  задовольняють умові задовольняють умові  Довести, що Довести, що 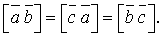 Доведення: Оскільки  то вектори то вектори  , ,  і і  утворюють трикутник. Згідно з означенням векторного добутку вектори утворюють трикутник. Згідно з означенням векторного добутку вектори  перпендикулярні до площини трикутника і всі вони спрямовані в один бік: перпендикулярні до площини трикутника і всі вони спрямовані в один бік: Знайдемо модулі кожного з визначених векторів: 


Маємо:  , тому що кожний з виразів дорівнює подвійній площі трикутника АВС. Таким чином, усі три вектори , тому що кожний з виразів дорівнює подвійній площі трикутника АВС. Таким чином, усі три вектори  однаково спрямовані та мають однакову довжину, тобто: однаково спрямовані та мають однакову довжину, тобто: 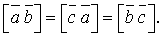
| 



 і кінцем у точці
і кінцем у точці  позначається символом
позначається символом  (або однією буквою
(або однією буквою  ,
,  , ...).
, ...). і позначається,
і позначається,  ,
,  .
. .
. .
. .
. ), якщо вони однаково спрямовані і мають рівні довжини.
), якщо вони однаково спрямовані і мають рівні довжини. , що з'єднує початок вектора
, що з'єднує початок вектора 
 на число
на число  називається вектор, який має довжину
називається вектор, який має довжину  і який має напрям вектора
і який має напрям вектора  та протилежний напрямок у разі
та протилежний напрямок у разі  .
. ; 2)
; 2)  .
.

 складає кут
складає кут  з віссю
з віссю  .
. (рис.1), взятої зі знаком «плюс», якщо напрям вектора
(рис.1), взятої зі знаком «плюс», якщо напрям вектора  збігається з напрямком осі і зі знаком «мінус» у противному випадку.
збігається з напрямком осі і зі знаком «мінус» у противному випадку. на вісь
на вісь  .
.
 вектора
вектора  .
. або,
або,  де
де  - одиничні вектори координатних осей
- одиничні вектори координатних осей  .
. і
і  , то його координати обчислюються за формулами:
, то його координати обчислюються за формулами: .
. і
і 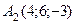 . Знайдіть координати і довжину вектора
. Знайдіть координати і довжину вектора  .
. ,
,  ,
,  ,
,  ,
,  ,
,  . Значить,
. Значить,  .
. .
. и
и  . Знайдіть координати і довжину вектора
. Знайдіть координати і довжину вектора  .
. ;
;  ;
; ;
; .
. з початком координат прямокутної системи координат
з початком координат прямокутної системи координат  . Нехай
. Нехай  - кути, які утворює вектор
- кути, які утворює вектор 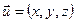 з осями координат
з осями координат  ,
,  ,
,  , для яких справедливі рівності:
, для яких справедливі рівності: ,
,  .
. 
 між ними (див. рис.3):
між ними (див. рис.3):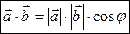 .
.

 .
. або
або  . (*)
. (*) — переставний (комутативний) закон.
— переставний (комутативний) закон. — розподільний закон.
— розподільний закон. .
.
 (або
(або  чи
чи 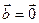 ).
).

 ,
,  або
або  ,
,  , то
, то .
. .
. 
 .
. :
: .
. . Знаючи, що
. Знаючи, що  и
и  , обчисліть
, обчисліть  .
.

 .
. Приклад 5. Дано вершини трикутника
Приклад 5. Дано вершини трикутника  ,
,  и
и  .Знайдіть: 1) внутрішній кут при вершині
.Знайдіть: 1) внутрішній кут при вершині 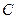 ;
;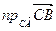 .
.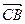 и
и  .
. ;
; .
.
 Т.е.
Т.е. 
 .
. і
і  називається вектор
називається вектор  , який задовольняє таким умовам:
, який задовольняє таким умовам: (37).
(37). та
та  (38).
(38). або
або  (39).
(39). якщо
якщо  (40).
(40). і векторний добуток їх дорівнює нуль-вектору, тобто
і векторний добуток їх дорівнює нуль-вектору, тобто (41).
(41). не виконується, або точніше вектор
не виконується, або точніше вектор  має напрям, протилежний до
має напрям, протилежний до  (42).
(42). (43).
(43). (44).
(44). (45).
(45).
 і
і 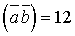 . Обчислити
. Обчислити  .
. . Для того, щоб розв’язати задачу, нам потрібно знайти
. Для того, щоб розв’язати задачу, нам потрібно знайти  . З умови
. З умови  маємо:
маємо:  , звідки
, звідки  =
= 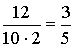 . Оскільки
. Оскільки  .
. :
: 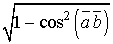 =
=  .
. .
.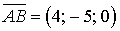 та
та 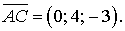 Тоді згідно з формулою
Тоді згідно з формулою  та формулою (45) дістанемо:
та формулою (45) дістанемо:
 , тобто
, тобто  Отже, знаходимо
Отже, знаходимо  і маємо
і маємо 
 та
та  були колінеарними?
були колінеарними?
 ,
,
 і
і  , отже
, отже  звідки
звідки  або
або  , тобто вектори
, тобто вектори  Довести, що
Довести, що 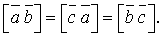
 перпендикулярні до площини трикутника і всі вони спрямовані в один бік:
перпендикулярні до площини трикутника і всі вони спрямовані в один бік:


 , тому що кожний з виразів дорівнює подвійній площі трикутника АВС. Таким чином, усі три вектори
, тому що кожний з виразів дорівнює подвійній площі трикутника АВС. Таким чином, усі три вектори