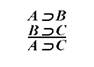ПОЗНАВАТЕЛЬНОЕ

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Індуктивні умовиводи та їх види

Індукцією називається умовивід, у якому на основі знання частини предметів класу робиться висновок про всі предмети класу, про клас у цілому. Індукція — це умовивід від часткового до загального. Термін "індукція" походить під латинського слова inductio, що означає "наведення".

Індукція, як і будь-який умовивід, складається із засновків і висновку. Засновки в індукції — це судження про окремі факти, одиничні предмети або групи предметів і явищ. Висновок — судження про клас предметів або явищ у цілому.

Будується індуктивний умовивід так. У процесі пізнання предметів якогось класу ми виявляємо, що кожен предмет, який спостерігаємо, має ознаку Р. Під час подальшого спостереження предметів цього класу ми відмічаємо, що й вони мають ті самі ознаки. Не досліджуючи останніх предметів класу, ми робимо узагальнюючий висновок, що всі предмети цього класу мають ознаки Р.

Розрізняють декілька видів індуктивних умовиводів. Серед них: 1) повна індукція; 2) неповна індукція.

Повна індукція — це такий індуктивний умовивід, у якому загальний висновок про клас предметів робиться на підставі вивчення всіх предметів даного класу.

Індуктивний умовивід застосовується тільки в тих випадках, коли ми маємо справу із закритими класами предметів: число предметів, що до них входять, є скінченним і вони повинні легко піддаватися перерахуванню.

Неповна індукція — це такий вид індуктивного умовиводу, у якому загальний висновок щодо ознак предметів всього класу робиться в результаті дослідження лише частини предметів даного класу.

Розрізняють такі види неповної індукції: індукція через простий перелік, індукція через відбір фактів і наукова індукція

Індукція через простий перелік фактів — це такий умовивід, у якому загальний висновок про клас предметів робиться на тій підставі, що серед фактів, що спостерігаються, не трапляється жодного, який би суперечив узагальненню. Цей умовивід характеризується тим, що досліджуються не всі предмети певного класу, а тільки відомі. Висновок буде вважатись достовірним доти, поки не буде виявлений факт, який йому суперечить.

Індукція через відбір фактів — це такий індуктивний умовивід, в якому загальний висновок про клас предметів робиться на основі деяких предметів даного класу, але відібраних із загальної маси за певним принципом, що робить неможливим їх випадкове співпадіння.

Наукова індукція — це індуктивний умовивід, в якому загальний висновок про всі предмети класу робиться на підставі знання необхідних ознак або причинних зв'язків частини предметів класу.

Умовно-розділові умовиводи

Безпосередні умовиводи

Під безпосередніми умовиводами розуміють такі умовиводи, у котрих висновок робиться всього з одного засновку. Так, якщо висловимо судження "Будь-який злочин є правопорушення" і з нього зробимо висновок про те, що "Деякі правопорушення є злочинами", то цей розумовий процес є умовиводом безпосереднім.

Висновок у безпосередньому умовиводі ми здобуваємо за допомогою перетворення судження. Проте безпосередній умовивід не може бути зведеним до простої зміни однієї лише форми судження, він зачіпає і зміст думки, робить її визначенішою, яснішою, точнішою. Цим вихідне знання оновлюється, набуває іншого звучання. Безпосередній умовивід є за формою умовиводом, а не перетворенням судження, як твердять дехто з логіків. Йому притаманні всі ознаки умовиводу: у ньому наявне вихідне знання, знання висновкове і знання обґрунтовуюче — ті правила, за якими вихідне судження перетворюється у висновкове.

Основними способами побудови безпосередніх умовиводів є перетворення, обернення та протиставлення суджень. Безпосередні умовиводи утворюють також за допомогою зіставлення суджень за правилами відношень між судженнями

Перетворення

Перетворення — це така операція, унаслідок якої вихідне судження перетворюється у судження рівнозначне за змістом, але іншої структури. Наприклад: "Будь-який договір е угода; отже, жоден договір не є неугода".

Схема перетворення суджень:

· Усі S є Р -> Жодне S не є не-Р.

· Деякі S є Р -> Деякі S не є не-Р.

· Жодне S не є S -> Усі S є не-Р.

· Деякі S не є Р—>Деякі S є не-Р

Перетворення — найпростіша форма утворення безпосереднього умовиводу. У висновковому судженні розуміється те ж відношення між поняттями, що й у вихідному судженні. Але перетворене судження категоричніше, думка в ньому виражена настільки визначено й однозначно, що тлумачити її інакше просто неможливо.

Обернення

Оберненням називається така операція, коли суб'єкт вихідного судження стає предикатом, а предикат — суб'єктом вивідного судження. Наприклад: "Будь-який договір є юридичною угодою, отже, деякі юридичні угоди — договори".

Схеми:

· S-P -> P-S

· Жодне S не є Р->Жодне Р не є S.

· Деякі S є P->Деякі Р є S.

· Тільки деякі S є Р — Усі Р є S.

Під час обернення якість судження не змінюється: якщо вихідне судження є ствердним, то й висновок буде ствердним, якщо ж засновок заперечний, то й висновок буде заперечним. Кількість судження може змінюватися, але може залишатися тією ж.

Обернення буде простим (або чистим), якщо кількість судження під час обернення не змінюється. Приклад такого обернення: "Деякі студенти — відмінники; отже," деякі відмінники — студенти". Тут кількість оберненого судження залишалася такою ж, якою вона була у вихідному судженні: "Деякі S є -Р" перетворилося у судження "Деякі Р е S",

Обернення з обмеженням — це таке обмеження, унаслідок якого змінюється кількість судження. Наприклад: "Усі капіталісти експлуататори; отже, деякі експлуататори — капіталісти". У цьому умовиводі вихідне судження є загальним ("Усі S є Р" а висновкове — частковим ("Деякі Р є S").

Обернення умовних суджень

Розрізняють два види обернення умовних суджень: контрпозицію і конверсію.

Контрпозиція умовного судження полягає в тім, що ми заперечуємо підставу і наслідок вихідного умовного судження, а потім наслідок робимо підставою, а підставу — наслідком оберненого судження. Наприклад: "Якщо угода не відповідає умовам закону, то вона не дійсна; отже, якщо угода визнана дійсною, то вона відповідає закону". Схема контрпозиції умовного судження така:

Якщо А, то В. Отже якщо не В а не А

Конверсією називається обернення умовних виділяючих і одиничних умовних суджень. Конверсія умовних суджень полягає в тому, що наслідок вихідного судження робиться основою, а основа — наслідком вивідного судження. Наприклад: "Якщо межі необхідної оборони не перевищені, то кримінальна відповідальність за заподіяне не настає; отже, якщо карна відповідальність за заподіяне при необхідній обороні не настає, то межі необхідної оборони не перевищені". Схема обернення таких суджень:

Якщо А, то В. Отже, Якщо В, то А, або А ~ В -> В ~ А.

Протиставлення предикату

Протиставленням предикату називається висновок такого нового судження, суб'єктом котрого є поняття, що суперечить предикату вихідного судження, а предикатом — суб'єкт вихідного судження. Наприклад: "Будь-який злочин е діяння суспільно небезпечне; отже, жодне не суспільно небезпечне діяння не є злочином".

Тут суб'єктом висновкового судження є не просто предикат вихідного судження ("діяння суспільно небезпечне"), а поняття, що суперечить предикату ("не суспільно небезпечне діяння"). Предикатом у цьому умовиводі є суб'єкт вихідного судження — поняття "злочин". Схема протиставлення предикату така:

· S є Р, отже не Р не є S

· Всі S є Р->Жодне не Р не є S.

· Жодне S не є Р->Деякі не Р є S.

· Деякі S не є Р->Деякі не Р є S.

Протиставлення — це складніша, ніж перетворення і обернення, форма безпосереднього умовиводу. Протиставлення є синтез перетворення і обернення, необхідно вихідне судження спочатку перетворити, а потім перетворене судження обернути

Умовні умовиводи

Умовні умовиводи завжди включають до свого складу як перший засновок умовне судження. Залежно від того, якими судженнями (умовними, категоричними чи розділовими) є другий засновок і висновок, умовні судження поділяються на суто умовні, умовно-категоричні та умовно-розділові.

У м о в н о - к а т е г о р и ч н и м називається умовивід, у якому один засновок умовне судження, а другий засновок і висновок категоричні судження.

Існує два різновиди умовно-категоричного умовиводу:

- modus ponens і

- modus tollens.

Розглянемо "modus ponens" .

У перекладі з латинської мови "modus ponens означає "від ствердження підстави до ствердження наслідку".

Наприклад,

Якщо гіпотеза підтверджується на практиці, то вона стає теорією. Дана гіпотеза підтверджується практикою. Отже, вона перетворюється в теорію.

Мовою логіки висловлювань структуру цього міркування можна записати у вигляді правила висновку:

Ч и с т о у м о в н и м називається умовивід у якому засновки і висновок є умовними судженнями.

Наприклад,

Якщо студент здібний, то він має досягнення у науковій роботі. Якщо студент має досягнення у науковій роботі, то його можна рекомендувати до вступу в аспірантуру.

Отже, якщо студент здібний, то його можна рекомендувати до вступу в аспірантуру.

Логічну структуру цього умовиводу представляє така формула:

У логіці висловлювань ця формула є правилом висновку, яке називається "транзитивністю імплікації":

Ум о в н о -р о з д і л о в и м умовиводом називається умовивід, у якому один із засновків є розділовим судженням, а решта умовними судженнями.

Наприклад,

Якщо ранкові газети повідомлять про результати референдуму, то я ще сьогодні зможу підготуватися до виступу. Якщо вечірні газети повідомлять про результати референдуму, то я лише завтра зможу підготуватися до виступу. Результати референдуму повідомлять або ранкові, або вечірні газети.

Отже, я зможу підготуватися до виступу або сьогодні, або завтра.

Умовно-розділові умовиводи мають ще одну назву - лематичні. Ця назва походить від грецького слова lemma - припущення. Така назва зумовлена тим, що вона випливає з тієї характеристики умовиводів, що розглядають різні припущення та їх наслідки.

В залежності від кількості альтернатив у розділовому засновку лематичні умовиводи поділяють на:

а) дилеми (дві альтернативи);

б) трилеми (три альтернативи);

в) полілеми (чотири і більше альтернатив).

У практиці міркувань найчастіше використовують дилеми, тому зупинимося на їх аналізі.

За якістю наслідку (заперечувальний або стверджувальний) дилеми поділяють на:

- конструктивні та

- деструктивні.

За складністю наслідку дилеми поділяють на:

- прості та

- складні.

К о н с т р у к т и в н о ю називається дилема у висновок якої входять наслідки умовних засновків.

Д е с т р у к т и в н о ю називається дилема, висновок якої складається із заперечення підстав умовних засновків.

П р о с т о ю називається дилема, висновком якої є наслідок умовного засновку, або заперечення підстави умовного засновку.

С к л а д н о ю називається дилема, висновком якої є диз'юнкція наслідків умовних засновків або заперечення підстав умовних засновків.