 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Базис булевых функций. Теорема Поста 12
Таблицы истинности функций Задана булева функция Отрицание, обозначение
Дизъюнкция (логическое или), обозначение
Сумма по модулю 2, обозначение
Построим таблицу истинности заданной функции.
Укажем существенные и фиктивные переменные булевой функции f. Вначале рассмотрим булеву переменную Аналогично рассмотрим оставшиеся булевы переменные. По переменной По переменной По переменной Таким образом, все переменные булевой функции являются существенными. Нормальные формы и полиномы Запишем по таблице истинности заданной функции совершенную дизъюнктивную нормальную форму (СДНФ). Для этого рассмотрим наборы, где функция принимает значение 1. В результате получим
Запишем по таблице истинности заданной функции совершенную конъюнктивную нормальную форму (СКНФ). Для этого рассмотрим наборы, где функция принимает значение 0 и возьмем каждый набор с отрицанием. В результате получим
Построим полином Жегалкина, рассмотрев наборы, где булева функция принимает значение 1, и воспользовавшись формулой
В формуле надо раскрыть скобки и упростить выражения с помощью соотношений Для заданной функции получим
Степень полинома – 3. Проверим правильность преобразований с помощью таблицы истинности.
Результат совпадает с исходной таблицей истинности. Все три представления булевой функции эквивалентны. Далее будем рассматривать булеву функцию в классе ДНФ и полиномов Жегалкина. Базис булевых функций. Теорема Поста Проверим элементарные булевы функции, входящие в состав заданной, на образование базиса.
В таблице знаком «+» обозначено принадлежность функции к данному классу. Для того чтобы функции составляли базис, по теореме Поста необходимо, чтобы хотя бы одна функция не сохраняла 0, хотя бы одна функция не сохраняла 1, хотя бы одна функция не была самодвойственной, хотя бы одна функция не была монотонной и хотя бы одна функция не была линейной. Из вышеприведенной таблицы видно, что данный набор функций составляет базис. Причем для базиса достаточно первых двух функций, то есть отрицания и дизъюнкции. Проверим возможность получения из заданной булевой функции f путем суперпозиции некоторой булевой функции По таблице истинности
Построим по таблице истинности двойственную функцию
Исходя из таблицы истинности Рассмотрим два набора Степень полинома Жегалкина для заданной функции f равняется 3, поэтому Заданная функция f принадлежит к функционально полному в слабом значении классу, так как она немонотонная и нелинейная. Поэтому добавление констант 0 и 1 в класс 12 |



 . Рассмотрим таблицы истинности для элементарных булевых функций, входящих в нее.
. Рассмотрим таблицы истинности для элементарных булевых функций, входящих в нее. :
: :
:

 :
:






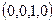 и
и 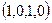 , которые являются соседними по этой переменной.
, которые являются соседними по этой переменной.  ,
,  ,
,  . Т.е. переменная
. Т.е. переменная  рассмотрим два набора
рассмотрим два набора 
 ,
,  .
. рассмотрим два набора
рассмотрим два набора 
 ,
,  .
. рассмотрим два набора
рассмотрим два набора 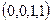
 ,
, 
 .
. .
. ,
,  ,
,  .
.








 . Для этого проверим f на принадлежность классам Поста.
. Для этого проверим f на принадлежность классам Поста. , следовательно
, следовательно  .
. , следовательно
, следовательно  .
. , значения которой можно получить из значений функции f с помощью инвертирования (т.е. переписывания в обратном порядке) и поэлементного отрицания.
, значения которой можно получить из значений функции f с помощью инвертирования (т.е. переписывания в обратном порядке) и поэлементного отрицания.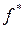
 , следовательно
, следовательно  .
. и
и  . Согласно лексикографического порядка
. Согласно лексикографического порядка  , но
, но  . Поэтому
. Поэтому  .
. .
.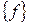 позволит получить из f путем суперпозиции любую булеву функцию
позволит получить из f путем суперпозиции любую булеву функцию