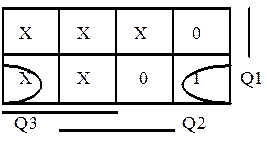ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Проектирование синхронных счетчиков-делителей частоты на JK-триггерах 12
Синхронные счетчики имеют много общего с асинхронными счетчиками, рассмотренными на предыдущем занятии. Так общее определение синхронного счетчика аналогично определению асинхронного. При этом также различают коэффициенты пересчета (модуль счета) Основным отличием синхронных счетчиков от асинхронных заключается в способе переключения триггеров счетчика. Если в асинхронных счетчиках каждый последующий триггер переключается только после того как переключится предыдущий, то в синхронных счетчиках все триггеры переключаются одновременно, сигнал синхронизации поступает на все триггеры счетчика параллельно. Для получения необходимого модуля счета синхронного счетчика также требуется соответствующее количество триггеров, которое в общем случае рассчитывается по формуле
При этом следует учитывать тот факт, что n может быть нецелым. В этом случае следует округлить n до ближайшего целого большего n. В общем смысле количество триггеров может быть и большим, чем определенное по приведенной формуле, однако кроме ряда специальных применений такие счетчики будут нерациональными. Внутреннее состояние счетчика определяется состоянием его триггеров. При этом различают младшие и более старшие триггеры счетчика состояния которых, как правило, взвешены по двоичному закону. Так младший триггер имеет вес 1, более старший - вес 2, еще более старший - 4 и т.д. Состояние счетчика, например, 9 означает что первый, самый младший триггер счетчика находится в состоянии 1, второй триггер - в состоянии 0, третий - 0, четвертый - 1, остальные, если они присутствуют, имеют состояние 0. Изменение состояния счетчика означает изменение состояния его триггеров. При этом различают счетчики с естественным порядком счета и произвольным порядком счета. В счетчиках с естественным порядком счета под действием тактовых импульсов синхронизации состояния счетчика каждый раз изменяются на единицу - вес самого младшего триггера. Для суммирующих счетчиков состояние увеличивается, для вычитающих - уменьшается. В счетчиках с произвольным порядком счета каждый приходящий тактовый импульс может переводить счетчик в произвольное состояние из всех
1 - 3 - 15 - 8 - 1 - 3 - 15 - 8 и т. д.
Синтезировать подобные счетчики можно используя JK-триггеры, которые под действием импульсов синхронизации могут принимать различные состояния, определяемые режимом работы, задаваемым управляющими сигналами J и K. JK-триггер имеет следующее обозначение(рис.4.1).
Таблица переключений такого триггера выглядит следующим образом
0 0 0 0 режим хранения
0 1 0 0 режим сброса
1 0 0 1 режим усьановки
1 1 0 1 счетный режим 1 1 1 0
Триггеры могут иметь большее количество входов управления J и K, объединенных логикой И, а также дополнительные входы асинхронного сброса R и установки S. Обозначение триггера в этом случае выглядит следующим образом:
Рис. 3 JK - триггер с логикой 3И по входам J и K, а также со входами приоритетного сброса и установки
Как видно из таблицы состояние триггера на текущем такте k зависит от состояния его входов J и K на предыдущем такте k-1 и от собственно состояния триггера также на предыдущем такте. При этом можно сделать следующие обобщающие выводы: - триггер на текущем такте принимает состояние входа J на предыдущем такте, если состояние самого триггера на предыдущем такте было равно нулю; - состояние триггера на текущем такте не зависит от состояния его входа J на предыдущем такте если состояние самого триггера на предыдущем такте было равно единице; - триггер на текущем такте принимает состояние входа не-К на предыдущем такте, если состояние самого триггера на предыдущем такте было равно единице; - состояние триггера на текущем такте не зависит от состояния его входа К на предыдущем такте, если состояние самого триггера на предыдущем такте было равно нулю.
Сказанное проиллюстрируем диаграммой
J = Qk, если Qk-1 = 0 J = X . если Qk-1 = 1 __ K = Qk, если Qk-1 = 1 K = X , если Qk-1 = 0
Руководствуясь этой диаграммой, можно синтезировать синхронные счетчики с произвольным порядком счета. Рассмотрим, например, синхронный счетчик со следующим порядком счета
...- 4 - 1 - 2 - 0 - 5 - 7 - 6 - 4 - 1 - 2 - ...
Модуль счета такого счетчика равен 7. Количество триггеров, необходимое для реализации такого счетчика равно трем. Максимальное состояние счетчика равно 7, что не противоречит количеству применяемых триггеров. Составим сводную таблицу переключений триггеров счетчика, в которой будут отражены состояния триггеров счетчика на текущем k такте, состояния триггеров счетчика на предыдущем k-1 такте и состояния его информационных входов J и K, которые определяются согласно приведенной выше диаграмме.
Таблица 7
Далее для каждой функции J и K каждого из триггеров составим карты Вейча и проведем минимизацию логических функций
J3
J2
J1
K3
K2
K1
После минимизации всех шести логических функций для каждого информационного входа J и K каждого триггера получим переключательные функции ___ ___ ___ J3 = Q1 * Q2 J2 = Q1 J1 = Q2
___ ___ ___ ___ K3 = Q1 * Q2 K2 = Q1 K1 = Q2 + Q3 Согласно приведенным выражениям построим принципиальную схему синхронного счетчика
Рис. 3 Принципиальная схема синхронного счетчика с произвольным порядком счета
Таким образом, мы синтезировали принципиальную схему синхронного счетчика с заданным порядком счета. Триггеры в таком счетчике будут переключаться согласно приведенной выше сводной таблице переключений триггеров. Задаваясь, таким образом, требуемым законом переключения, можно синтезировать конечный автомат призванный решать конкретные задачи.
Задание:
1. Синтезировать счетчик импульсов сл следующим порядком счета
2. Синтезировать дешифратор натурального 4-хразрядного двоичного кода в семисегментный полный (0,1,2,…d. E, F) 3. Синтезировать дешифратор 4-хразрядного двоичного кода специального назначения (см. задание № 1) в семисегментный полный (0,1,2,…d. E, F), при этом (например для варианта 1) вместо цифры «С (12)» должна отображаться цифра «0», вместо «3» — «1» и т.д. 4. Синтезировать схему счетчика плюс схемы обоих дешифраторов в пакете MAX+II 5. Сформировать генератор тактовых импульсов для счетчика частотой следования ~ 0,3 Гц 6. Произвести симуляцию и запрограммировать ПЛИС.
СПИСОК ЛИТЕРАТУРЫ
1. Титце У., Шенк К. Полупроводниковая схемотехника: Справочное руководство. Пер. с нем.-М.: Мир, 1982. 2. Хоровиц П., Хилл У. Искусство схемотехники: В 2-х томах. Пер. с англ.- М.: Мир, 1983. 3. Ерофеев Ю.Н. Импульсные устройства: Учеб. пособие для вузов по спец. “Радиотехника”.- 3-е изд., перераб. и доп.- М.: Высш. шк., 1989.
12 |



 - количество тактовых импульсов синхронизации, которое необходимо подать на тактовый вход счетчика для того, чтобы он вернулся в исходное состояние.
- количество тактовых импульсов синхронизации, которое необходимо подать на тактовый вход счетчика для того, чтобы он вернулся в исходное состояние.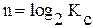 .
. возможных. При этом общее число возможных состояний, которые последовательно принимает счетчик, составляют модуль счета. Состояния счетчика в пределах его модуля счета не могут повторяться. При этом модуль счета может быть существенно ниже максимального состояния счетчика. Например, счетчик может иметь модуль счета равный 4, в то время как его максимальное состояние может быть равным 15, т.е. с одной стороны для обеспечения требуемого модуля счета требуется всего два триггера, с другой для обеспечения максимального состояния - четыре. Порядок счета у такого счетчика может быть следующим
возможных. При этом общее число возможных состояний, которые последовательно принимает счетчик, составляют модуль счета. Состояния счетчика в пределах его модуля счета не могут повторяться. При этом модуль счета может быть существенно ниже максимального состояния счетчика. Например, счетчик может иметь модуль счета равный 4, в то время как его максимальное состояние может быть равным 15, т.е. с одной стороны для обеспечения требуемого модуля счета требуется всего два триггера, с другой для обеспечения максимального состояния - четыре. Порядок счета у такого счетчика может быть следующим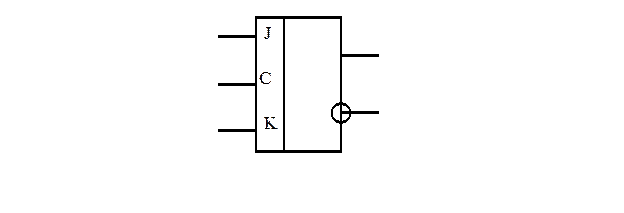 Рис. 4.1 Простой JK - триггер
Рис. 4.1 Простой JK - триггер Таблица 6
Таблица 6 J K Qk-1 Qk
J K Qk-1 Qk 0 0 1 1
0 0 1 1 0 1 1 0
0 1 1 0 1 0 1 1
1 0 1 1