 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Минимизация Логических Функций 12
Методические указания к выполнению курсового проекта
Минимизация Логических Функций В цифровой технике задача, как правило, формулируется в форме таблицы переключений, которая называется также таблицей истинности. Прежде всего, требуется найти такую логическую функцию, которая соответствовала этой таблице. На следующем этапе эту функцию преобразуют в простейшую форму, которую потом реализуют с помощью соответствующей комбинации базовых логических схем. Логические функции записывают, как правило, в дизъюнктивно нормальной форме. Преобразование функции в простейшую форму - минимизацию - можно осуществить последовательно применяя правила и законы булевой алгебры. Однако этот путь не всегда оказывается простым, особенно если число входных независимых переменных больше трех. Важнейшим вспомогательным средством для определения наиболее простой логической функции является таблица Карно (часто в литературе описывают ее разновидность - диаграмму Вейча). Это не что иное, как измененная запись таблицы переключений. В этом случае значения входных переменных не просто записываются рядом друг с другом, а размещаются по горизонтали и вертикали таблицы, деля ее, наподобие шахматной доски, на отдельные квадраты. При четном количестве входных переменных половину из них записывают по горизонтали, а половину - по вертикали. При нечетном числе переменных по горизонтали размещается на одну переменную больше, чем по вертикали (или наоборот). Порядок размещения различных комбинаций значений входных переменных следует выбирать таким, чтобы при переходе от одной ячейки к соседней изменялась лишь одна переменная. В эти ячейки заносятся те значения выходной функции y, которые соответствуют значениям входных переменных (по таблице истинности). В качестве примера приведена таблица истинности 1 для функции “И” и соответствующая ей таблица Карно 2. Таблица Карно является лишь упрощенной формой записи таблицы истинности, поэтому на ее основании можно составить дизъюнктивно нормальную форму искомой логической функции, пользуясь описанным выше методом. Преимуществом таблиц Карно является простота Таблица1
Таблица 2
обнаружения возможных упрощений логической функции. Рассмотрим это на примере, представленном в таблице истинности 3 и соответствующей ей таблице Карно 4. Таблица 3
Таблица 4
В первую очередь при составлении дизъюнктивной нормальной формы следует, руководствуясь общим правилам записи переключательной функции, составить логическое произведение всех входных переменных для каждой ячейки, в которой стоит единица. Для ячейки, расположенной в левом верхнем углу, получается
Для ячейки, расположенной правее, седует записать
Когда наконец будет составлена логическая сумма всех произведений, помимо других в ней встретится и такой фрагмент:
Он упрощается следующим образом:
Отсюда следует общее правило упрощения логических функций для таблиц Карно: Если в двух, четырех, восьми и т.д. ячейках, ограниченных прямоугольным или квадратным контуром, стоят только единицы, можно записывать непосредственно логическое произведение для всей этой группы, причем в это произведение должны входить лишь те входные переменные, которые остаются неизменными для всех ячеек данной группы. Таким образом, в этом примере логическое произведение для группы B, состоящей из двух ячеек, равно
что соответствует ранее полученной функции. В одну группу связываются также те ячейки, которые находятся на левом и правом краях одной строки или в верхней и нижней частях одного столбца (см. группу А, обозначенную на таблице Карно разрывной линией). Для столбца D, состоящего из четырех ячеек, можно записать
Для контура С, имеющего квадратную форму и состоящего также из четырех элементов, получим следующее логическое произведение:
Еще одна единица осталась в правом верхнем углу. Она может быть связана, например, с единицей в нижней части рассматриваемого столбца в группу
Для дизъюнктивно нормальной формы стазу найдем максимально упрощенный результат :
При минимизации логической функции с помощью таблицы Карно следуе помнить несколько простых правил, непосредственно вытекающих из цели минимизации - получении наиболее простой переключательной функции, содержащей минимально возможное количество слагаемых дизъюнктивной нормальной формы с минимально возможным рангом слагаемых - количеством входных независимых переменных в слагаемом. В этом смысле любое обединение в группу отдельно стоящей ячейки таблицы Карно, в которой выходная функция y принимает единичное значение, дает запись одного слагаемого выходной переключательной функции вместо двух, четырех, восьми и т.д. (по количеству объединяемых в группу ячеек) с сокращением на одну, две, три и т.д. входных независимых переменных, или другими словами понижением ранга слагаемого. Однако здесь не следует увлекаться и объединять все встречаемые ячейки подряд, поскольку можно, тем самым произвести лишнюю группировку. Рассмотрим это на примере таблицы Карно 2.5, несколько отличающейся от заданной первоначально. Руководствуясь приведенными выше соображениями здесь, как и в предыдущем примере следует объединить ячейки в группы D и C. Такое объединение дает при формировании переключательной функции вместо восьми слагаемых четвертого ранга два слагаемых второго ранга. Оставшиеся две ячейки, в которых выходная функция y принимает единичное значение можно объединить в группы А, В и Е так как это показано на таблице 2.5. Однако каждое такое объединение в группу дает одно дополнительное слагаемое выходной переключательной функции, усложняя последнюю. Вместе с тем, оставляя не тронутым объединение в группу А и убрав объединения в группы В и Е, можно получить одно
Таблица 5
единственное слагаемое третьего ранга соответствующее группе А, причем в этом случае каждая из ячеек таблицы, в которых выходная функция у принимает единичное значение, хотя бы один раз участвуют в группировке, т.е. дает минимизацию переключательной функции. Другими словами допускается группировка типа “звезда”, когда одна ячейка (группа ячеек) группируется с другими ячейками (группами ячеек) многократно, как это видно на примере левой верхней ячейки таблицы 2.4. С другой стороны не допускается группировка типа “цепочка”, когда группируются ячейки (группы ячеек) каждая из которых ранее уже участвовала в группировках. В любой группировке ячеек должна быть хотя бы одна, участвующая только в этой группировке. Таким образом можно получать минимальную дизъюнктивную нормальную переключательную функцию любого числа переменных.
12 |
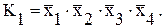
, содержащую две ячейки. Другая возможность состоит в объединении единиц, находящихся на левом и правом краях первой строки. Однако если принять во внимание, что в каждом углу таблицы Карно находится единица, то можно найти простейшее решение. Связывая эти единицы в одну четырехэлементную группу, получим
,
.