 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Описание критерия аппроксимации и способа его минимизации. 12
Постановка задачи. При изучении зависимостей между величинами важной задачей является приближенное представление (аппроксимация) этих зависимостей с помощью известных функций или их комбинаций, подобранных надлежащим образом. Подход к такой задаче и конкретный метод ее решения определяются выбором используемого критерия качества приближения и формой представления исходных данных. Пусть изучается связь между величинами C и U, из которых первая рассматривается в качестве независимой переменной, а вторая – ее функции. Исходные данные представлены значениями U, заданными на некотором множестве M значений X. Тогда ошибка приближения этой зависимости некоторой аппроксимирующей функции y = j (x) для каждого из значений X может быть оценена разностью d = y - j (x) , x Î M . Значения y = yi заданы для конечного множества (n) значений xi , di = d (xi ) = yi – j (xi) , ( i =1, 2, …, n) .
На основе изучения ошибок d формируются различные критерии качества аппроксимации, служащие для определения наилучшей аппроксимирующей функции j (x). Один из распространенных подходов опирается на использование метода наименьших квадратов (МНК), в соответствии с которым наилучшей считается такая аппроксимирующая функция j (x), для которой достигается наименьшее значение суммы квадратов ошибок d во всех точках x, принимаемых во внимание. Это требование принимает вид
В настоящей курсовой работе исходные данные заданы в виде табличной зависимости yi (xi). Уточним условия МНК для этой задачи. Задача. Зависимость между переменными x и y задана их значениями в отдельных точках Наилучшая аппроксимирующая функция
Подобное задание исходных данных встречается в задачах технических измерений и их статистической обработки, когда для каждого из задаваемых значений
Представление исходных данных.
Описание критерия аппроксимации и способа его минимизации. Аппроксимирующую функцию φ(x) выбирают из некоторого семейства функций, для которого задан вид функции, но остаются неопределенными (и подлежат определению) ее параметры С1, С2, …, Сm , т.е. j (x) = j (x, С1, С2,…, Сm) . (2) Для решения задачи подставим выражение (2) в выражение (1) и проведем необходимые операции суммирования. В результате величина J , критерий аппроксимации, представится функцией искомых параметров J = J(С1, С2, …, Сm) . (3) Последующие действия сводятся к отысканию минимума этой функции J переменных Сk . Определение значений Сk = Сk* , k = 1, 2, …, m , соответствующих этому минимуму J,и является целью решаемой задачи. Поскольку величина J неотрицательна (как сумма квадратов) и нижняя ее граница есть 0 (J=0), то, если существующее решение системы единственно, оно отвечает именно минимуму J. Уравнения, встречающиеся в МНК, называются нормальными, поэтому описываемый способ решения задачи условимся называть методом нормальных уравнений. Структура этих уравнений получается более простой в том важном частном случае, когда аппроксимирующая функция j(x) выбирается линейной функцией искомых параметров Сk и выражение (2) имеет вид
где Сk – определяемые параметры; j1(x), j2(x),…, jm(x) – система некоторых линейно-независимых функций, называемых в курсовой работе базисными функциями. Замечание. Функции j1(x), j2(x),…, jm(x) называются линейно-независимыми, если при любых x равенство
справедливо только тогда, когда все Сk =0.
В этом случае, подставляя (4) в выражение (1) и выполняя дифференцирование, получим систему уравнений относительно искомых Сk . Покажем получение системы нормальных уравнений в общем случае для m базисных функций. Раскроем выражение аппроксимирующей функции j(x) = С1 j1(x) + С2 j2(x) +…+ Сm jm(x) и подставим его в формулу критерия аппроксимации.
Применим операцию дифференцирования к параметру С1 :
12 |
(i=1, 2,…, n). Тогда для каждого из этих значений определена и ошибка (см.рисунок)
.
, 
. Требуется найти функцию 
, наилучшим образом (МНК) аппроксимирующую указанную зависимость.
должна быть определена из условия
. (1)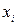
осуществляется измерение величины 
(сопровождающееся возможными ошибками). Аппроксимация позволяет представить изучаемую связь между x и y с помощью известных функций, что облегчает последующее использование данных, кроме того позволяет «сгладить» возможные ошибки измерений, а также дает возможность оценивать значения переменной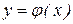 
в точках x интервала 
, не совпадающих с заданными (т.е. решать задачу интерполяции).
(4)
.