 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса - ваш вокал
Игровые автоматы с быстрым выводом
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший "Салат из свеклы с чесноком"
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
 Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
 Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
| Определение по кривой разгона передаточной функции объекта методом М.П. Симою (метод площадей)
Передаточная функция объекта определяется как произведение двух передаточных функций  и и  . График представлен в виде переходной характеристики . График представлен в виде переходной характеристики  , где , где  . Кривая разгона объекта с самовыравниванием без транспортного запаздывания. . Кривая разгона объекта с самовыравниванием без транспортного запаздывания. 1. На кривой разгона (Приложение 1) ось абсцисс разбиваем на равные отрезки с интервалом времени  . При выборе величины отрезка . При выборе величины отрезка  следует учесть: следует учесть: а) кривая разгона на участке  должна мало отличаться от прямой; должна мало отличаться от прямой; б) чем меньше  , тем более точным будет конечный результат. Однако с уменьшением интервала разбиения резко возрастает объем вычислений, а излишне высокая точность вычисления может не дать желаемого результата. , тем более точным будет конечный результат. Однако с уменьшением интервала разбиения резко возрастает объем вычислений, а излишне высокая точность вычисления может не дать желаемого результата. 20,50 Вариант Задания 
2. Значения  в конце каждого интервала в конце каждого интервала  делим на делим на  и получившиеся значения и получившиеся значения  заносим в таблицу 2.1. заносим в таблицу 2.1. Таблица 2.1.  | h(i) |  |  | 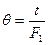 | | | | | | | 1.66 | 0.166 | 0.834 | 0.276 | | 3.99 | 0.399 | 0.601 | 0.551 | | 5.66 | 0.566 | 0.434 | 0.827 | | 6.66 | 0.666 | 0.334 | 1.102 | | 7.52 | 0.752 | 0.248 | 1.378 | | 8.33 | 0.833 | 0.167 | 1.653 | | 8.66 | 0.866 | 0.134 | 1.929 | | 8.99 | 0.899 | 0.101 | 2.205 | | 9.22 | 0.922 | 0.078 | 2.480 | | 9.33 | 0.933 | 0.067 | 2.756 | | 9.51 | 0.951 | 0.049 | 3.031 | | 9.66 | 0.966 | 0.034 | 3.307 | | 9.77 | 0.977 | 0.023 | 3.582 | | 9.82 | 0.982 | 0.018 | 3.858 | | 9.93 | 0.993 | 0.007 | 4.133 | | | | | 4.409 | | | | | 4.685 | | | | | 4.960 | | | | | 5.236 | 3. Вычисляем значение 4-го столбца и записываем в таблицу 2.1.
4. Определяем площадь  по формуле: по формуле:  , (2.1) , (2.1)
где  - сумма 4-го столбца (1). Сумма 4-го столбца равна 4.129. - сумма 4-го столбца (1). Сумма 4-го столбца равна 4.129. 
5. Функцию  перестраиваем в другом масштабе времени, за независимую переменную берем время перестраиваем в другом масштабе времени, за независимую переменную берем время 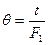 , значения которой также записываем в таблицу 2.1. , значения которой также записываем в таблицу 2.1. 6. Заполняем таблицу 2.2 (столбцы 1 и 2 переписываем из таблицы 2.1). Таблица 2.2  |  |  |  |  | 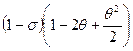 | | | | | | | | 0.276 | 0.834 | 0.724 | 0.604 | 0.486 | 0.405 | | 0.551 | 0.601 | 0.449 | 0.270 | 0.05 | 0.03 | | 0.827 | 0.434 | 0.173 | 0.075 | -0.312 | -0.135 | | 1.102 | 0.334 | -0.102 | -0.034 | -0.597 | -0.199 | | 1.378 | 0.248 | -0.378 | -0.094 | -0.807 | -0.2 | | 1.653 | 0.167 | -0.653 | -0.109 | -0.94 | -0.157 | | 1.929 | 0.134 | -0.929 | -0.124 | -0.997 | -0.134 | | 2.205 | 0.101 | -1.205 | -0.122 | -0.979 | -0.099 | | 2.480 | 0.078 | -1.480 | -0.115 | -0.885 | -0.069 | | 2.756 | 0.067 | -1.756 | -0.118 | -0.714 | -0.048 | | 3.031 | 0.049 | -2.031 | -0.099 | -0.469 | -0.022 | | 3.307 | 0.034 | -2.307 | -0.078 | -0.146 | -0.005 | | 3.582 | 0.023 | -2.582 | -0.059 | 0.251 | 0.006 | | 3.858 | 0.018 | -2.858 | -0.051 | 0.726 | 0.013 | | 4.133 | 0.007 | -3.133 | -0.022 | 1.275 | 0.009 | | 4.409 | | -3.409 | | 1.902 | | | 4.685 | | -3.685 | | 2.605 | | | 4.960 | | -3.960 | | 3.381 | | | 5.236 | | -4.236 | | 4.236 | | 7. Определяем площади  и и 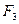 по формулам: по формулам:  , (2.2) , (2.2)
где  - сумма 4-го столбца. - сумма 4-го столбца.  , (2.3) , (2.3)
где  - сумма 6-го столбца. - сумма 6-го столбца. Сумма 4-го столбца равна 0,924, а сумма 6-го столбца равна 0,022. 

Так как 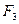 отрицательная, то прекращаем дальнейшие исчисления отрицательная, то прекращаем дальнейшие исчисления 8. Тип передаточной функции выбираем по виду кривой разгона, исходя из следующих предпосылок: если значение регулируемой величины при  равна нулю, но производная не равна нулю, то порядок числителя передаточной функции на единицу меньше порядка знаменателя: равна нулю, но производная не равна нулю, то порядок числителя передаточной функции на единицу меньше порядка знаменателя:  , (2.4) , (2.4)
При расчете ограничимся всего тремя площадями:  , ,  , , 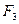 . В этом случае имеем уравнения: . В этом случае имеем уравнения:  , (2.5) , (2.5)
Если в этом случае передаточная функция принимает вид (2.4), то получим  . .
В этом случае  и уравнение (2.5) примет вид: и уравнение (2.5) примет вид:  , (2.6) , (2.6)
В этих уравнениях 5 неизвестных. Для того, чтобы не было не определенности, рекомендуется вычислить площади  и и  . С учетом того, что . С учетом того, что  , ,  , ,  , ,  , получим 5 уравнений, необходимых для вычислений 5 неизвестных. , получим 5 уравнений, необходимых для вычислений 5 неизвестных. Так как получится громоздкое решение, остановимся на передаточной функции 2-го порядка:  , (2.7) , (2.7)
При нашей передаточной функции (2.7)  , ,  , ,  система уравнений (2.6) примет вид: система уравнений (2.6) примет вид: 
9. Определим коэффициенты выбранной передаточной функции путем решения системы уравнений (2.6):  , ,  , ,  10. Получаем передаточную функцию вида  . .
ЛИТЕРАТУРА 1. Яковлев Ю.С. Локальные системы автоматики: Текст лекций. – Чебоксары: Изд-во Чуваш. ун-та,1993.- 176с.
|




 и
и  . График представлен в виде переходной характеристики
. График представлен в виде переходной характеристики  , где
, где  . Кривая разгона объекта с самовыравниванием без транспортного запаздывания.
. Кривая разгона объекта с самовыравниванием без транспортного запаздывания. . При выборе величины отрезка
. При выборе величины отрезка  должна мало отличаться от прямой;
должна мало отличаться от прямой;
 в конце каждого интервала
в конце каждого интервала  и получившиеся значения
и получившиеся значения  заносим в таблицу 2.1.
заносим в таблицу 2.1.


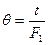
 по формуле:
по формуле: , (2.1)
, (2.1) - сумма 4-го столбца (1). Сумма 4-го столбца равна 4.129.
- сумма 4-го столбца (1). Сумма 4-го столбца равна 4.129.




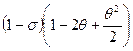
 и
и 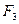 по формулам:
по формулам: , (2.2)
, (2.2) - сумма 4-го столбца.
- сумма 4-го столбца. , (2.3)
, (2.3) - сумма 6-го столбца.
- сумма 6-го столбца.

 равна нулю, но производная не равна нулю, то порядок числителя передаточной функции на единицу меньше порядка знаменателя:
равна нулю, но производная не равна нулю, то порядок числителя передаточной функции на единицу меньше порядка знаменателя: , (2.4)
, (2.4) , (2.5)
, (2.5) .
. и уравнение (2.5) примет вид:
и уравнение (2.5) примет вид: , (2.6)
, (2.6) и
и  . С учетом того, что
. С учетом того, что  ,
,  ,
,  ,
,  , получим 5 уравнений, необходимых для вычислений 5 неизвестных.
, получим 5 уравнений, необходимых для вычислений 5 неизвестных. , (2.7)
, (2.7) ,
,  система уравнений (2.6) примет вид:
система уравнений (2.6) примет вид:
 ,
,  ,
, 
 .
.