 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Производная неявной функции 12
Неявной называется функция вида F(x, y) = 0. Пример 8. Найти производную функции, заданную уравнением
и вычислить ее значение в точке ( 1, 2 ). Решение. Дифференцируем уравнение по х, учитывая, что y = f(x). В результате получим Отсюда находим производную функции
Затем вычисляем ее значение при х = 1 и у = 2
2.3. Применение дифференциального Если имеется неопределенность вида
Пример 9. (Пример Лопиталя). Найти предел отношения двух функций:
и Решение. Очевидно, что То есть имеем неопределенность вида Для нахождения предела применяем правило Лопиталя. Найдем производные этих функций.
=
Учитывая, что х ® а, окончательно получим
Пример 10. Найти предел Решение. Обозначим
Очевидно, что имеется неопределенность вида
= Окончательно получим
Пример 11. Найти предел Решение. Применяя правило Лопиталя, получим
ПРИЛОЖЕНИЯ Приложение 1 Таблица производных некоторых функций 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. Приложение 2 Индивидуальные контрольные задания Вариант № 1 1.Построить графики функций:
2.Задана числовая последовательность:
Требуется: 2.1. Записать 6 членов этой числовой последовательности; 2.2. При e = 0,1; при e = 0,01 и при e = 0,001 найти такой номер N (для каждого значения e ), что все члены последовательности, начиная с n > N оказываются внутри границы A - e < x < A + e . 3.Доказать, что
Найти хо и d для значений e : e = 0,2; e = 0,02. 4.Найти пределы функций в бесконечности и в точке: 4.1. 4.2. 4.3.
5.Найти пределы функций двумя способами: - преобразованием и дальнейшим сокращением слагаемых числителя и знаменателя; - применяя правило Лопиталя. 5.1. 5.2. 6.Найти пределы: 6.1. 6.2. 7.Найти производные функций: 7.1. 7.2. 7.3. 8.Найти производные двумя способами: - по правилам дифференцирования; - с помощью логарифмирования. 8.1. 8.2. 8.3. 9.Найти производную функции заданную уравнением
и вычислить ее значение при x = 1/2 ; y =2. Вариант № 2 1.Построить графики функций:
2.Задана числовая последовательность:
Требуется: 2.1. Записать 6 членов этой числовой последовательности; 2.2. При e = 0,1; при e = 0,01 и при e = 0,001 найти такой номер N (для каждого значения e ), что все члены последовательности, начиная с n > N оказываются внутри границы A - e < x < A + e . 3.Доказать, что 3.1. Найти хо и d для значений e: e = 0,2; e = 0,02. 4.Найти пределы функций в бесконечности и в точке: 4.1. 4.2. 4.3. 5.Найти пределы функций двумя способами: - преобразованием и дальнейшим сокращением слагаемых числителя и знаменателя; - применяя правило Лопиталя. 5.1. 5.2. 6.Найти пределы: 6.1. 6.2. 7.Найти производные функций: 7.1. 7.2. 7.3. 8.Найти производные двумя способами: - по правилам дифференцирования; - с помощью логарифмирования. 8.1. 8.2. 8.3. 9.Найти производную функции заданную уравнением
и вычислить ее значение при x = 1 ; y =2. Вариант № 3 1.Построить графики функций:
2.Задана числовая последовательность
Требуется: 2.1. Записать 6 членов этой числовой последовательности; 2.2. При e = 0,1; при e = 0,01 и при e = 0,001 найти такой номер N (для каждого значения e ), что все члены последовательности, начиная с n > N оказываются внутри границы A - e < x < A + e .
3.Доказать, что 3.1. 3.2. Найти хо и d для значений e: e = 0,2; e = 0,02 . 4.Найти пределы функций в бесконечности и в точке: 4.1. 4.2. 4.3. 5.Найти пределы функций двумя способами: - преобразованием и дальнейшим сокращением слагаемых числителя и знаменателя; - применяя правило Лопиталя. 5.1. 5.2. 6.Найти пределы: 6.1. 6.2. 7.Найти производные функций: 7.1. 7.2. 7.3. 8.Найти производные двумя способами: - по правилам дифференцирования; - с помощью логарифмирования. 8.1. 8.2. 8.3. 9.Найти производную функции заданную уравнением:
и вычислить ее значение при x = 1; y =2. Вариант № 4 1.Построить графики функций:
2.Задана числовая последовательность Требуется: 2.1. Записать 6 членов этой числовой последовательности; 2.2. При e = 0,1; при e = 0,01 и при e = 0,001 найти такой номер N (для каждого значения e ), что все члены последовательности, начиная с n > N оказываются внутри границы A - e < x < A + e . 3. Доказать, что: 3.1. Найти хо и d для значений e: e = 0,2; e = 0,02. 4. Найти пределы функций в бесконечности и в точке: 4.1. 4.2. 4.3. 5.Найти пределы функций двумя способами: - преобразованием и дальнейшим сокращением слагаемых числителя и знаменателя; - применяя правило Лопиталя. 5.1. 5.2. 6.Найти предел: 6.1. 6.2. 7.Найти производные функций: 7.1. 7.2. 7.3. 8.Найти производные двумя способами: - по правилам дифференцирования; - с помощью логарифмирования. 8.1. 8.2. 8.3. 9.Найти производную функции заданную уравнением:
и вычислить ее значение при x = 1/2; y =2. Вариант № 5 1.Построить графики функций:
2.Задана числовая последовательность
Требуется: 2.1. Записать 6 членов этой числовой последовательности; 2.2. При e = 0,1; при e = 0,01 и при e = 0,001 найти такой номер N (для каждого значения e ), что все члены последовательности, начиная с n > N оказываются внутри границы A - e < x < A + e . 3.Доказать, что 3.1. 3.2. Найти хо и d для значений e : e = 0,2; e = 0,02 . 4.Найти пределы функций в бесконечности и в точке: 4.1. 4.2. 4.3. 5.Найти пределы функций двумя способами: - преобразованием и дальнейшим сокращением слагаемых числителя и знаменателя; - применяя правило Лопиталя. 5.1. 5.2. 6.Найти пределы: 6.1. 6.2. 7.Найти производные функций: 7.1. 7.2. 7.3. 8.Найти производные двумя способами: - по правилам дифференцирования; - с помощью логарифмирования. 8.1. 8.2. 8.3. 9.Найти производную функции заданную уравнением
и вычислить ее значение при x = 2; y = 1. Вариант № 6 1.Построить графики функций
2.Задана числовая последовательность
Требуется: 2.1. Записать 6 членов этой числовой последовательности; 2.2. При e = 0,1; при e = 0,01 и при e = 0,001 найти такой номер N (для каждого значения e ), что все члены последовательности, начиная с n > N оказываются внутри границы A - e < x < A + e . 3.Доказать, что: 3.1. 3.2. Найти хо и d для значений e: e = 0,2; e = 0,02 . 4.Найти пределы функций в бесконечности и в точке: 4.1. 4.2. 4.3. 5.Найти пределы функций двумя способами: - преобразованием и дальнейшим сокращением слагаемых числителя и знаменателя; - применяя правило Лопиталя. 5.1. 5.2. 6.Найти пределы: 6.1. 6.2. 7.Найти производные функций: 7.1. 7.2. 7.3. 8.Найти производные двумя способами: - по правилам дифференцирования; - с помощью логарифмирования. 8.1. 8.2. 8.3. 9. Найти производную функции заданную уравнением:
и вычислить ее значение при x = 1; y =2. Вариант № 7 1.Построить графики функций:
2.Задана числовая последовательность
Требуется: 2.1. Записать 6 членов этой числовой последовательности; 2.2. При e = 0,1; при e = 0,01 и приe = 0,001 найти такой номер N (для каждого значения e ), что все члены последовательности, начиная с n > N оказываются внутри границы A - e < x < A + e . 3.Доказать, что: 3.1. 3.2. Найти хо и d для значений e: e = 0,2; e = 0,02. 4.Найти пределы функций в бесконечности и в точке. 4.1. 4.2. 4.3. 5.Найти пределы функций двумя способами: - преобразованием и дальнейшим сокращением слагаемых числителя и знаменателя; - применяя правило Лопиталя. 5.1. 5.2. 6.Найти пределы: 6.1. 6.2. 7.Найти производные функций: 7.1. 7.2 7.3.
8.Найти производные двумя способами: - по правилам дифференцирования; - с помощью логарифмирования. 8.1. 8.2. 8.3. 9.Найти производную функции заданную уравнением
и вычислить ее значение при x = 1/2; y =2. Вариант № 8 1.Построить графики функций
2.Задана числовая последовательность
Требуется: 2.1. Записать 6 членов этой числовой последовательности; 2.2. При e = 0,1; при e = 0,01 и приe = 0,001 найти такой номер N (для каждого значения e ), что все члены последовательности, начиная с n > N оказываются внутри границы A - e < x < A + e . 3.Доказать, что: 3.1. 3.2. Найти хо и d для значений e: e = 0,2; e = 0,02. 4.Найти пределы функций в бесконечности и в точке: 4.1. 4.2. 4.3. 5.Найти пределы функций двумя способами: - преобразованием и дальнейшим сокращением слагаемых числителя и знаменателя; - применяя правило Лопиталя. 5.1. 5.2. 6.Найти пределы: 6.1. 6.2. 7.Найти производные функций: 7.1. 7.2. 7.3. 8.Найти производные двумя способами: - по правилам дифференцирования; - с помощью логарифмирования. 8.1. 8.2. 8.3. 9.Найти производную функции заданную уравнением
и вычислить ее значение при x = 1/2; y =2. Вариант № 9 1. Построить графики функций
2.Задана числовая последовательность
Требуется: 2.1. Записать 6 членов этой числовой последовательности; 2.2. При e = 0,1; при e = 0,01 и приe = 0,001 найти такой номер N (для каждого значения e ), что все члены последовательности, начиная с n > N оказываются внутри границы A - e < x < A + e. 3. Доказать, что: 3.1. 3.2. Найти хо и d для значений e: e = 0,2;e = 0,02. 4.Найти пределы функций в бесконечности и в точке: 4.1. 4.2. 4.3. 5.Найти пределы функций двумя способами: - преобразованием и дальнейшим сокращением слагаемых числителя и знаменателя; - применяя правило Лопиталя. 5.1. 5.2. 6.Найти пределы: 6.1. 6.2. 7.Найти производные функций: 7.1. 7.2. 7.3. 8.Найти производные двумя способами: - по правилам дифференцирования; - с помощью логарифмирования. 8.1. 8.2. 8.3. 9.Найти производную функции заданную уравнением
и вычислить ее значение при x = 1; y =2. Вариант № 10 1.Построить графики функций:
2.Задана числовая последовательность
Требуется: 2.1. Записать 6 членов этой числовой последовательности; 2.2. При e = 0,1; при e = 0,01 и при e = 0,001 найти такой номер N (для каждого значения e ), что все члены последовательности, начиная с n > N оказываются внутри границы A - e < x < A + e . 3.Доказать, что: 3.1. 3.2. Найти хо и d для значений e : e = 0,2; e = 0,02 . 4.Найти пределы функций в бесконечности и в точке: 4.1. 4.2. 4.3. 5.Найти пределы функций двумя способами: - преобразованием и дальнейшим сокращением слагаемых числителя и знаменателя; - применяя правило Лопиталя. 5.1. 5.2. 6.Найти пределы: 6.1. 6.2. 7.Найти производные функций: 7.1. 7.2. 7.3. 8.Найти производные двумя способами: - по правилам дифференцирования; - с помощью логарифмирования. 8.1. 8.2. 8.3. 9.Найти производную функции заданную уравнением
и вычислить ее значение при x = 1/2; y =2. Вариант № 11 1.Построить графики функций:
2.Задана числовая последовательность
Требуется: 2.1. Записать 6 членов этой числовой последовательности; 2.2. При e = 0,1; при e = 0,01 и при e = 0,001 найти такой номер N (для каждого значения e ), что все члены последовательности, начиная с n > N оказываются внутри границы A - e < x < A + e. 3.Доказать, что: 3.1. 3.2. Найти хо и d для значений e: e = 0,2; e = 0,02 . 4.Найти пределы функций в бесконечности и в точке. 4.1. 4.2. 4.3. 5.Найти пределы функций двумя способами: - преобразованием и дальнейшим сокращением слагаемых числителя и знаменателя; - применяя правило Лопиталя. 5.1. 5.2. 6.Найти пределы: 6.1. 6.2. 7.Найти производные функций: 7.1. 7.2. 7.3. 8.Найти производные двумя способами: - по правилам дифференцирования; - с помощью логарифмирования. 8.1. 8.2. 8.3. 9.Найти производную функции заданную уравнением
и вычислить ее значение при x = 1/2; y =2.
Таблица 1 Таблица вариантов контрольных заданий
©2015 www.megapredmet.ru Все права принадлежат авторам размещенных материалов. |




 .
. .
. .
. или
или  , то
, то
 .
.
 при
при  .
. .
. = =
= =  =
= ;
; =
= 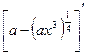 =
=  = =
= =  =
=  .
. =
=  =
=  =
=  .
. .
. и
и 
 =
=  =
= ;
;  .
. =
=  =
=  .
. .
. =
=  =
=  =
=  = =
= =  =
=  = 2.
= 2.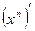 =
=  ;
; =
= 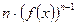 ×
× 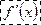 ;
; =
=  ;
; =
=  ×
×  ;
; =
=  ;
; =
=  ×
×  ;
; =
=  ;
; =
=  ×
×  =
=  ;
; =
=  ;
; =
=  ;
; =
= 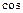
 ×
×  ;
; =
=  ;
; ;
; ;
; =
=  ;
;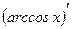 =
=  ;
; =
=  ;
; =
=  .
. ;
; ;
; ;
; ;
; ;
; ;
; ;
;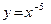 ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
. .
. ;
;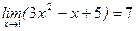 .
. ;
; ;
; .
. ;
; .
. ;
; .
. ;
; ;
; .
.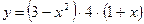 ;
; ;
;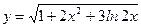 .
.
 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
;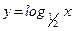 ;
; ;
; ;
; .
. .
. ; 3.2.
; 3.2.  .
. ;
; ;
; .
. ;
; .
. ;
; .
. ;
; ;
; .
.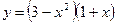 ;
; ;
; .
.
 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
;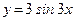 ;
; ;
; .
. .
. ;
; .
. ;
; ;
; .
. ;
; .
. ;
; ;
; .
. ;
; ;
; .
.
 ;
; ;
; ;
; ;
; ;
; ;
; ;
;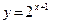 ;
; ;
;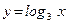 ;
; ;
; ;
; .
. .
.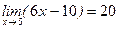 ; 3.2.
; 3.2.  .
. ;
; ;
; .
. ;
; .
. ;
; ;
;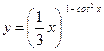 .
. ;
;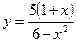 ;
; .
. .
. ;
; ;
; ;
; ;
; ;
;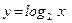 ;
; ;
; .
. ;
; .
. ;
; ;
; ;
; .
. ;
; .
. ;
; ;
;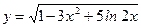 .
.
 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
;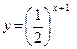 ;
; ;
; ;
; .
. .
. ;
; .
. ;
; ;
; ;
; .
. ;
; ;
; .
. ;
;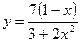 ;
; .
.
 ;
; ;
; ;
;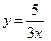 ;
; ;
; ;
; ;
; ;
; ;
; ;
;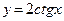 ;
; .
. ;
; .
. ;
; ;
; ;
;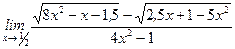 .
. ;
; ;
; ;
; .
. ;
; ;
; .
.
 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
. .
. ;
; .
. ;
; ;
; ;
;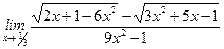 .
. .
. ;
; .
. ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
;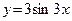 ;
;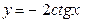 ;
; .
. .
. ;
; .
. ;
; ;
;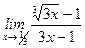 ;
; .
. ;
; ;
; .
. ;
;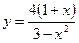 ;
;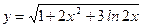 .
.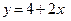 ;
; ;
; ;
; ;
; ;
; ;
; ;
;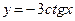 ;
; .
. .
.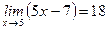 ;
; .
. ;
; ;
; ;
; .
. .
. ;
; ;
; .
. ;
; ;
; ;
; ;
; ;
;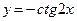 .
. .
.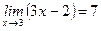 ;
; .
. ;
; ;
; .
. .
. ;
; .
.