 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Построение графиков функций 12
ББК 22.161.Я72
Ó Институт рыночной экономики, социальной политики и права, 2012. СОДЕРЖАНИЕ ВВЕДЕНИЕ.. 5 ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ИЗУЧЕНИЮ ДИСЦИПЛИНЫ 6 РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА.. 8 ПРОГРАММА ДИСЦИПЛИНЫ ТЕМА 1. Введение в математический анализ. 9 Методические указания. 9 Контрольные вопросы по теме. 10 ТЕМА 2. Дифференциальное исчисление. 11 Методические указания. 11 Контрольные вопросы по теме. 11 МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ИНДИВИДУАЛЬНОГО КОНТРОЛЬНОГО ЗАДАНИЯ.. 13 1. Примеры выполнения заданий по теме 1 1.1. Построение графиков функций. 14 1.2. Числовая последовательность. Предел числовой последовательности 19 1.3. Пределы функций. 21 2. Примеры выполнения заданий по теме 2 "Дифференциальное исчисление" 27 2.1. Основные правила дифференцирования. 28 2.2. Производная неявной функции. 33 2.3. Применение дифференциального исчисления; правило Лопиталя 34 ПРИЛОЖЕНИЯ.. 36 Таблица производных некоторых функций. 36 Индивидуальные контрольные задания по вариантам.. 38 Вариант № 1. 38 Вариант № 2. 40 Вариант № 3. 42 Вариант № 4. 45 Вариант № 5. 47 Вариант № 6. 49 Вариант № 7. 52 Вариант № 8. 54 Вариант № 9. 57 Вариант № 10. 59 Вариант № 11. 61 Таблица вариантов контрольных заданий. 64 Образец титульного листа контрольного задания. 65 ВВЕДЕНИЕ Программа раздела "Математический анализ" рассчитана на освоение предмета в форме заочного обучения. Данный раздел изучается на 1-м курсе в течение 2-х семестров. По окончании каждого семестра выполняется контрольная работа и сдается зачет. В методических указаниях даны общие рекомендации по работе с учебно-методическими материалами (лекции, раздаточный материал, учебные пособия), а также рекомендации по изучению каждой темы и выполнению контрольных заданий. Цели и задачи дисциплины, ее место в учебном процессе Математика имеет важное методологическое значение в системе подготовки современного экономиста. Изучение экономики требует хорошей математической подготовки, позволяющей свободно ориентироваться в экономической литературе, насыщенной различными математическими приемами, решать практические задачи, прогнозировать события в экономической сфере. Цельюматематического образования является развитие: u навыков математического мышления; u навыков использования математических методов и основ математического моделирования; u математической культуры у обучающегося. В результате изучения раздела "Математический анализ" студенты должны: а) иметь представление u о математическом множестве и функциональных зависимостях; u о дифференциальном и интегральном исчислении; б) знать u основные математические понятия и конструкции; в) уметь u производить операции над множествами, строить и анализировать графики основных функций; u проводить анализ и оптимизацию функций различными методами применительно к экономическим задачам. ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ При заочной форме обучения большая часть времени, отводимого на освоение дисциплины, приходится на самостоятельную работу. Для повышения эффективности самостоятельной работы помимо лекций, читаемых в интенсивной форме, предусмотрен раздаточный материал с вопросами, подлежащими изучению, а также настоящие методические указания. Работа студента при изучении дисциплины включает: прослушивание лекций, изучение раздаточного материала, работу с рекомендуемой литературой с использованием методических указаний по каждой теме, выполнение контрольного задания и его защиту, подготовку к зачету и его сдачу. Раздел "Математический анализ" состоит из пяти тем и изучается студентами в течение двух семестров. На начальном семестре (нулевой семестр) изучаются темы: Часть I Тема 1. Введение в математический анализ. Тема 2. Дифференциальное исчисление. На следующем (первом) семестре изучаются темы: Часть II Тема 3. Применение дифференциального исчисления для исследования функций и построения их графиков. Тема 4. Интегральное исчисление. Тема 5. Дифференциальные уравнения. Системы дифференциальных уравнений. Все темы дисциплины студенты заочного обучения прорабатывают самостоятельно по учебникам и учебным пособиям. По основным вопросам студенты слушают обзорные лекции. Изучать дисциплину рекомендуется в следующей последовательности: 1. Ознакомиться с программой; 2. Прочитать методические указания; 3. Прочитать конспект лекций; 4. Изучить соответствующие разделы учебника; 5. Ответить на вопросы для самоконтроля при изучении каждой темы; 6. Выполнить задания контрольной работы и представить ее в институт до начала контрольного семестра. Рекомендуется в процессе изучения материала составить конспект, в который занести основные положения каждой изучаемой темы, разобрать самостоятельно и решить рассматриваемые примеры и задачи. В качестве основы следует брать конспект лекций, так как на лекциях раскрываются все темы и порядок их изучения. Для лучшего понимания материала следует изучить соответствующие разделы рекомендуемых учебников и ответить на вопросы, предлагаемые в конце каждой темы. Ответы на вопросы для самоконтроля должны содержать полный, исчерпывающий ответ. В настоящее время нет недостатка в учебниках и учебных пособиях по математическому анализу. Ниже приведен список основной и дополнительной литературы. В методических указаниях по каждой теме даны ссылки на определенные страницы этой литературы. Дополнительная литература служит для углубленного изучения вопроса и для самостоятельного выполнения индивидуального контрольного задания. РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА Основная 1. Высшая математика для экономистов: Учебн. пособие для вузов / Н. Ш. Кремер, Б. А. Тришин, М. Н. Фридман; Под ред. проф. Н. Ш. Кремера. – М.: Банки и биржи, ЮНИТИ, 1997. Дополнительная 2. Замков О. О., Толстопятенко А. В., Черемных Ю. Н. Математические методы анализа экономики. – М.: ДИС, 1997. 3. Калесников А. Н. Краткий курс математики для экономистов. – М.: ИНФРА-М, 1997. 4. Справочник по математике для экономистов / Под редакцией В. И. Ермакова. – М.: Высшая школа, 1997. 5. Карасев А. И., Савельева Т. Н. Математические методы и модели в планировании. – М.: Экономика, 1987. 6. Руководство к решению задач с экономическим содержанием по курсу высшей математики. / Под ред. А. И. Карасева и Н. Ш. Кремера. – М.: ВЗФЭИ, 1989. 7. Фихтенгольц Г. М. Основы математического анализа. Т.1. – М.: 1964. 8. Пискунов Н. С. Дифференциальное и интегральное исчисление. – М., 1962. Методическая 9. Погорянский А. Г. Математика для экономистов. 10. Холомай Б. В. Пределы и дифференцирование. Методические указания к практическим занятиям по курсу "Высшая математика". – М.: Изд. МЭИ, 1992.
ПРОГРАММА ДИСЦИПЛИНЫ ТЕМА 1. Элементы теории множеств. Функции, их свойства и графики. Числовые последовательности, предел числовой последовательности. Сложные и обратные функции, их графики. Класс элементарных функций. Пределы функций. Непрерывность функций. Литература: [ 1, с. 123 — 175]. Методические указания Понятие множества принадлежит к числу первичных, т.е. не определяемых через более простые. Множество может обладать различными свойствами. Связь между различными множествами может определяться конкретной функцией. Функции могут записываться в виде математических знаков, математических таблиц, а для наглядности изображаться в виде графиков. Каждая функция обладает вполне определенными, присущими только ей, характерными свойствами. Существует вполне определенная классификация функций, которая отражает их характер и связь с другими функциями. При изучении пределов функций следует усвоить, что существуют числовые последовательности, которые имеют предел. Для функций этот предел может существовать как в бесконечности, так и в точке. Существуют вполне определенные признаки существования пределов, что доказывается соответствующими теоремами. Следует разобраться с понятием непрерывности функции, т.к. функции с таким свойством широко применяются в экономических расчетах. Следует рассмотреть конкретные примеры применения математических функций в экономике, решить самостоятельно предлагаемые в рекомендуемом учебнике задачи и упражнения. Контрольные вопросы по теме 1. Что включает понятие "множество" и какие действия над двумя множествами обеспечивают получение нового множества? 2. Что включает понятие "функция" и какие существуют способы задания функций? 3.Какими основными свойствами обладает функция? 4. Какие функции относятся к основным элементарным функциям? Рассмотрите эти функции в виде уравнений и графиков. 5. Что включает понятие "элементарная функция"? 6. Какие существуют приемы построения графиков функций с помощью преобразования элементарных функций? 7. Что такое предел числовой последовательности? 8. Что понимают под пределом функции в бесконечности и в точке? 9. Что такое бесконечно малые величины и каковы их свойства? 10.Что такое бесконечно большие величины? Их свойства. 11. Какие признаки говорят о существовании предела функции и какие теоремы доказывают существование пределов? 12. Какие функции имеют "замечательные" пределы? 13. Какие функции называют непрерывными и какими свойствами обладают функции, непрерывные в точке, а какими непрерывные на отрезке? ТЕМА 2. Дифференциал функции и его геометрический смысл. Производная функции, ее смысл. Правила нахождения производной и дифференциала. Дифференцирование функций, заданных параметрически. Точки экстремума функции. Теорема Ферма. Теоремы Ролля, Лагранжа, Коши, их применение. Производные высших порядков. Представление функций ехр(х), sin(х), соs(х), ln(1+х), (1+х)a по формуле Тейлора. Литература: [ 1, с. 176 — 211, 240 — 242]. Методические указания При изучении этой темы следует, прежде всего, разобраться с физическим смыслом процесса дифференцирования и сущности производной от математической функции, изучить правила вычисления производных и дифференцирования. Необходимо изучить и запомнить производные основных элементарных функций, т.к. они являются основой для дифференциального исчисления. При изучении теорем следует обратить внимание на следствия, вытекающие из каждой теоремы, т.к. носят они прикладной характер и существенно помогают при решении задач. Для лучшего усвоения сложного теоретического материала следует рассмотреть предлагаемые в учебнике конкретные практические задачи по применению производной, в т.ч. в экономике. Контрольные вопросы по теме 1. Что понимают под касательной к кривой? 2. Как определяют угловой коэффициент касательной к кривой в данной точке? 3. Что понимают под производной функции? 4. Какой геометрический смысл имеет производная? 5. Какая функция дифференцируется в точке, а какая в определенном промежутке? 6. Какая связь между непрерывностью функции и ее дифференцируемостью? 7. Какие существуют правила дифференцирования и следствия из них? 8. Какую особенность имеет производная сложной функции? 9. Какие производные имеют основные элементарные функции? 10. Что определяет теорема Ролля и каков ее геометрический смысл? 11. Что определяет теорема Логранжа и каков ее геометрический смысл? 12. Что определяет теорема Лопиталя и каков ее геометрический смысл? 13. Приведите примеры использования производной в экономике. МЕТОДИЧЕСКИЕ УКАЗАНИЯ Выполнение контрольного задания является отчетом студента о проделанной работе по усвоению учебного материала. Студенты, не выполнившие контрольного задания или получившие за его выполнение неудовлетворительную оценку, к зачету не допускаются. Контрольное задание является индивидуальным. Каждый студент выбирает из приведенного ниже перечня контрольных заданий свой индивидуальный вариант, исходя из начальной буквы своей фамилии и последней цифры шифра, который закреплен за студентом (приложение 2, табл. 1). Контрольное задание состоит из нескольких упражнений и задач по каждой изученной теме. При оформлении контрольного задания необходимо: u использовать листы бумаги формата А4 (рекомендуется в клетку), заполняя их только с одной стороны и оставляя поля: слева 3 см, сверху и снизу по 2,5 см, справа 1 — 1,5 см; u при печати текста на пишущей машинке или наборе на компьютере оставлять межстрочный интервал, равный 1,5 строки; u титульный лист контрольного задания выполнить в соответствии с образцом, приведенным в приложении 3. Страницы контрольного задания должны быть пронумерованы, а листы скреплены. 1. Примеры выполнения заданий по теме 1 "Введение в математический анализ" Построение графиков функций Задания по построению графиков функций имеют различный уровень сложности. Сначала даются простейшие графики, построение которых не требует нахождения максимумов, минимумов, точек перегиба и т.п. и может быть произведено по 2-м, 3-м точкам. К таким графикам относятся графики: прямой линии, гиперболы, а также степенной, показательной, логарифмической и тригонометрических функций. Пример 1. Дана функция:
Требуется построить ее график. Решение. Очевидно, что график этой функции прямая линия, которая в общем виде может быть представлена уравнением:
При x = 0; y = -5. При x = 2; y = 1. Наносим координаты этих двух точек на сетку координат (рис. 1) и, проведя через них прямую линию, получаем график заданной функции. Пример 2. Дана функция:
Требуется построить ее график. Решение. Из уравнения видно, что это гипербола, которая в общем виде представляется как
При x = –2,5 y = 1; при x = –0,5 y = 5; при x = +0,5 y = –5; при x = +2,5 y = –1. При построении кривых для удобства найденные значения координат сводятся в таблицу:
Наносим координаты этих точек на сетку координат (рис. 2) и, проведя через них соответствующие кривые, получаем график заданной гиперболы. Пример 3. Дана функция: Решение. Из уравнения видно, что это показательная функция, которая в общем виде представляется как
и постоянный коэффициент k = 2 (т.к. График показательной функции может быть построен по 3-м точкам. Зададимся некоторыми значениями x , подставляя которые в данное уравнение, находим соответствующее значение y. Занесем полученные результаты в таблицу:
Наносим координаты этих точек на сетку координат При построении графиков тригонометрических функций
Откладывая по оси абсцисс значения углов (или соответствующих им радиан), а по оси ординат значения этих функций, строим графики
 Аналогично строятся графики половинного аргумента
и двойного аргумента для для Пример 4.Дана функция:
1.2. Числовая последовательность. Дана числовая последовательность:
Требуется: 1) записать 5 — 6 членов этой последовательности; 2) найти предел А этой последовательности; 3) при заданном значении e = 0,003 найти такой номер N, что все члены последовательности, начиная с номеров Решение. Задаемся несколькими значениями n и находим 5 — 6 членов заданной в общем виде последовательности:
Известно, что В соответствии с определением предела числовой последовательности: если для любого (даже сколь угодно малого) e > 0 , существует такой номер N , что для всех членов последовательности с номерами n > N верно неравенство
Тогда А – есть предел последовательности. Для заданной последовательности это условие можно записать как неравенство
Числитель заданной последовательности принимает два значения (3 и 1). Для нахождения n следует брать большее значение. Докажем справедливость этого положения. Принимаем значение числителя равное 3 (т.е. большее значение). Отсюда
Проверим правильность полученного результата, рассчитав х1001 и х1002:
Для лучшего понимания данного примера и в подтверждение того, что надо брать большее значение числителя, посмотрим какой получится результат, если возьмем значение числителя равное 1 (т.е. меньшее значение). Отсюда
Но по определению n должно быть целым числом, т.е. n > 334. Проверим правильность полученного результата, рассчитав х335 и х336:
Второе условие при значении числителя, равном 1, не обеспечивает требуемого неравенства. (При выполнении контрольного задания по данной теме Вам следует рассмотреть оба значения числителя и сделать соответствующие выводы). Следовательно, определение N необходимо производить по значению числителя, равному 3 (т.е. наибольшему значению). Итак, N = 1000 и для всех n > N (1001, 1002, 1003, ...) выполняется неравенство (1). Что и требовалось найти. Пределы функций Пример 5. Доказать, что предел функции Решение. По условию мы имеем предел функции По определению: число А = 7 называется пределом функции при х ® х0, если для любого (даже сколь угодно малого) числа
выполняется условие Выберем значение e, например, e = 0,03. Тогда неравенство
Полученное неравенство совпадает с неравенством (2), где х0 = 2 и d = 0,01. Итак, мы доказали, что пределом функции При решении задач на нахождение пределов функции применяют теоремы о пределах [1, с. 153 — 156], [ 9, с. 16 — 17]. Пример 6. Найти предел функции
Решение.
Пример 7. Найти предел функции
Решение.
Решение задач по определению пределов различных функций значительно облегчает знание замечательных пределов. Замечательные пределы 1. 2. 3. где е = 2,718281828… — число Эйлера. Равенство 3 следует из равенства 2 путем замены у = 1/х . Пример 8. Найти предел функции
Решение. Определяем, можно ли данную функцию подвести к замечательному пределу. Можно, если разделить почленно слагаемые числителя функции f(x) на знаменатель x.
Теперь, воспользовавшись одной из теорем о пределах (а именно: предел произведения двух функций равен произведению пределов этих функций), получим
= Часто при вычислении пределов получаем неопределенности видов:
Одним из приемов при решении таких задач является разложение числителя или знаменателя на множители для дальнейшего сокращения дробей. Пример 9. Найти предел Решение. Имеем неопределенность вида Разложим числитель функции
Сокращая дробь на (x - 1) получим f(x) = x . Окончательно: Пример 10. Найти предел Решение. Очевидно, что
Имеем неопределенность вида Для нахождения предела сначала освободимся от радикалов, умножая числитель и знаменатель функции на выражение сопряженное числителю f(x) = =
Сокращая на (3 - х) , получим
Пример 11. Найти предел Решение. Имеем неопределенность вида Сначала освободимся от радикалов, проводя замену Тогда х = t3 и, если х ® 1/8 , то t ® 1/2 . В результате получим Находим предел Естественно, что такая замена не освободила нас от неопределенности вида
Теперь после сокращения дроби получим
Так как функция f (t) состояла из двух множителей:
Ответ: Пример 12. Решение. Видим, что Имеем неопределенность вида ¥·0. Определим, можно ли данный пример подвести к замечательному пределу. Для этого второе слагаемое представим в виде:
Заменим В результате замены получим Следовательно,
С учетом первого слагаемого данного примера, ответ: 2 + 3 = 5 .
2. Примеры выполнения заданий по теме 2 "Дифференциальное исчисление" Термин "производная" был введен Лагранжем на рубеже XVIII — XIX веков. Для обозначения производной употребляют символы: по Лейбницу — по Лагранжу —
1. Аргументу х дается приращение Dх 0 и находится приращение функции Dy = f(x + Dx) - f(x) 2. Составляется отношение
Пример 1. Найти производную функции Решение.Аргументу х даем приращение х + Dх и находим приращение функции
= a×[x2 + 2x×Dx + (Dx)2] – a×x2 = a×Dx (2x + Dx) . Составляем отношение
Пример 2. Найти производную функции Решение. (Предлагается проделать самостоятельно все действия, произведенные в примере 1 данной темы, и получить ответ). Ответ: В приведенных примерах видна закономерность дифференцирования (т.е. нахождения производной) степенной функции вида
где а — постоянный коэффициент; n — любое число.
Пример 3.Найти производную функции Решение. В заданном уравнении а = 2; n = 1/3. Производная равна:
Если в уравнении общего вида Следовательно, производная постоянной величины равна нулю. Решение задач по нахождению производной различных функций производится на основе известных правил дифференцирования, которые с пояснениями представлены ниже и для наглядности сведены в таблицу (приложение 1). 12 |



 .
. , где a0 = -5; a1 = 3.
, где a0 = -5; a1 = 3. Известно, что прямая линия может быть построена по двум точкам. Найдем две точки, через которые должна пройти эта прямая. Зададимся некоторыми значениями x , подставляя которые в данное уравнение, находим соответствующее значение y.
Известно, что прямая линия может быть построена по двум точкам. Найдем две точки, через которые должна пройти эта прямая. Зададимся некоторыми значениями x , подставляя которые в данное уравнение, находим соответствующее значение y.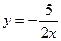 .
. , т.е. равнобочная гипербола, где а = -2,5.
, т.е. равнобочная гипербола, где а = -2,5. Учитывая, что график гиперболы располагается во 2-й и 4-й четвертях системы координат, для построения гиперболы необходимо иметь не менее 4-х точек, с положительными и отрицательными значениями координат. Зададимся некоторыми значениями x , подставляя которые в данное уравнение, находим соответствующее значение y.
Учитывая, что график гиперболы располагается во 2-й и 4-й четвертях системы координат, для построения гиперболы необходимо иметь не менее 4-х точек, с положительными и отрицательными значениями координат. Зададимся некоторыми значениями x , подставляя которые в данное уравнение, находим соответствующее значение y. .Требуется построить ее график.
.Требуется построить ее график.
 , где a = 2
, где a = 2 ).
). и
и  , желательно помнить их значения углов: 0о, 30о, 45о, 60о и 90о (и соответствующих им радиан: 0, p/6 , p/4 , p/3 , p/2 ). Сведем эти значения в таблицу.
, желательно помнить их значения углов: 0о, 30о, 45о, 60о и 90о (и соответствующих им радиан: 0, p/6 , p/4 , p/3 , p/2 ). Сведем эти значения в таблицу.
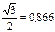

 (или
(или  )
)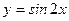 (или
(или  ). При этом следует помнить, что эти функции периодические с периодом
). При этом следует помнить, что эти функции периодические с периодом  . Тогда повторение значений функции будет:
. Тогда повторение значений функции будет: при x = 4p ;
при x = 4p ; . Требуется построить график этой функции.
. Требуется построить график этой функции. Решение. Построение графика производится исходя из закономерностей изменения элементарной функции, в данном случае синусоиды (рис. 5, кривая 1). Путем изменения значений аргумента трансформируем изначальную синусоиду в график функции
Решение. Построение графика производится исходя из закономерностей изменения элементарной функции, в данном случае синусоиды (рис. 5, кривая 1). Путем изменения значений аргумента трансформируем изначальную синусоиду в график функции  (рис. 5, кривая 2), а затем в график функции
(рис. 5, кривая 2), а затем в график функции 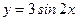 (рис. 5, кривая 3).
(рис. 5, кривая 3).
 .
. оказываются внутри границы
оказываются внутри границы  .
. ;
;  ;
;  ;
; ;
;  и т.д.
и т.д.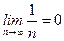 . Заданная числовая последовательность имеет подобный вид. Числитель заданной последовательности не превышает значения 3 , а знаменатель стремится к бесконечности. Таким образом, можно предположить, что предел заданной числовой последовательности А = 0 , но это требует доказательства.
. Заданная числовая последовательность имеет подобный вид. Числитель заданной последовательности не превышает значения 3 , а знаменатель стремится к бесконечности. Таким образом, можно предположить, что предел заданной числовой последовательности А = 0 , но это требует доказательства. или
или  .
. . (1)
. (1) , т.е.
, т.е.  или n > 1000 .
или n > 1000 . ;
;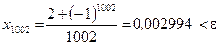 .
. , т.е.
, т.е.  или n > 333,333.
или n > 333,333. ;
; , т.е. требование нарушено.
, т.е. требование нарушено. при x ® 2 равен 7 (А = 7), т.е.
при x ® 2 равен 7 (А = 7), т.е.  ,
, , существует такое положительное число d, что для всех х, удовлетворяющих условию
, существует такое положительное число d, что для всех х, удовлетворяющих условию , (2)
, (2) (3)
(3) или
или  будет выполняться при
будет выполняться при  или, разделив левую и правую части неравенства на 3, получим
или, разделив левую и правую части неравенства на 3, получим .
. при х ® 2 является число А = 7, (см. определение предела функции).
при х ® 2 является число А = 7, (см. определение предела функции). при х ® - 1.
при х ® - 1. =
=  =
=  =
= =
=  = 7.
= 7. при х ® 2.
при х ® 2. =
=  =
=  =
=  = - 6.
= - 6. ;
; ;
; .
. при x®¥
при x®¥ =
=  .
. =
= ×
×  = е × 1 = е .
= е × 1 = е .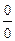 ;
;  ; ¥´0; ¥–¥ ; 00 ; ¥0 ; 1¥ .
; ¥´0; ¥–¥ ; 00 ; ¥0 ; 1¥ . .
. =
=  на множители
на множители .
. .
. .
. =
=  =
=  =
=  =
= =
=  .
. .
. .
. =
=  =
=  .
.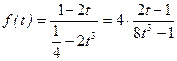 .
. =
=  =
=  .
. =
=  =
=  .
. , то искомый предел будет равен
, то искомый предел будет равен = 4
= 4  = 4×
= 4×  .
.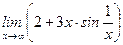 .
. .
. =
=  .
. (при х ® ¥, t ® 0 ).
(при х ® ¥, t ® 0 ). , где второй множитель является замечательным пределом (см. на с. 20 первый замечательный предел
, где второй множитель является замечательным пределом (см. на с. 20 первый замечательный предел  ).
). .
.

 Вычисление производной производится по алгоритму:
Вычисление производной производится по алгоритму: и находится предел этого отношения при Dх ® 0, т.е.
и находится предел этого отношения при Dх ® 0, т.е. =
=  =
= 
 .
. f(x+ Dx)
f(x+ Dx) f(x)
f(x) = a (2x + Dx);
= a (2x + Dx); . Ответ:
. Ответ:  .
. .
.
 ,
, .
. .
.
 .
.