 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Правило сложения дисперсий
Если совокупность разбита на группы по факторному признаку, то общая дисперсия признака
Общая дисперсияхарактеризует вариацию признака по всей совокупности как результат влияния всех факторов, определяющих индивидуальные различия единиц совокупности.
где х – индивидуальное значение признака;
n – число наблюдений в группе i.
Средняя из внутригрупповых дисперсийотражает ту часть вариации результативного признака, которая обусловлена действием прочих неучтенных факторов, кроме фактора, по которому осуществлялась группировка. Другими словами, внутригрупповая дисперсия отражает случайную вариацию.
Межгрупповая дисперсияхарактеризует вариацию, обусловленную влиянием фактора, положенного в основу группировки. Отношение межгрупповой дисперсии к общей дает возможность измерить вариацию результативного признака за счет факторного, то есть признака, положенного в основание группировки, и тем самым судить о связи между изучаемыми признаками:
где Корень квадратный из коэффициента детерминации называют эмпирическим корреляционным отношением:
Эмпирическое корреляционное отношение показывает какую часть общей колеблемости результативного признака определяет изучаемый фактор, т.е. характеризует влияние группировочного признака на результативный признак. Этот показатель принимает значения в интервале [0,1]. Если связь отсутствует, то Пример. С целью установления зависимости между урожайностью и сортом винограда в одном из хозяйств на основе выборки определили урожай на 10 кустах винограда:
Исчислите общую, межгрупповую и среднюю из групповых (частных) дисперсий. Определите связь между сортом и его урожайностью.
1. Групповые средние, т.е. средняя урожайность по каждому сорту винограда, равны:
2. Определяем среднюю урожайность винограда по хозяйству:
3. Определяем внутригрупповую (частную) дисперсию урожайности для каждого сорта отдельно:
4. Средняя из частных дисперсий:
5. Межгрупповая дисперсия:
6. Определяем общую дисперсию урожайности по всей совокупности, используя правило сложения дисперсий:
7. Проверим этот вывод путем расчета общей дисперсии обычным способом:
8. Определим коэффициент детерминации -
Таким образом, только на 26 % вариация урожайности обусловлена различиями между сортами, а на 74 % - другими факторами (характером почвы, удобренностью участков, поливом и т.п.) 9. Определяем эмпирическое корреляционное отношение:
Следовательно, можно утверждать, что связь умеренная. |



 может быть определена как сумма межгрупповой дисперсии
может быть определена как сумма межгрупповой дисперсии  и средней из внутригрупповых дисперсий
и средней из внутригрупповых дисперсий  :
:
 ,
, - дисперсия признака в группе i (внутригрупповая дисперсия);
- дисперсия признака в группе i (внутригрупповая дисперсия);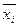 - среднее значение признака в группе i;
- среднее значение признака в группе i;
 где
где  - среднее значение признака в совокупности.
- среднее значение признака в совокупности.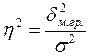 ,
, - коэффициент детерминации.
- коэффициент детерминации. .
.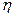 =0. В этом случае дисперсия групповых средних равна нулю (
=0. В этом случае дисперсия групповых средних равна нулю (  =0), т.е. все групповые средние равны между собой и межгрупповой вариации нет. Это означает, что группировочный признак не влияет на вариацию исследуемого признака х. Если связь функциональная, то
=0), т.е. все групповые средние равны между собой и межгрупповой вариации нет. Это означает, что группировочный признак не влияет на вариацию исследуемого признака х. Если связь функциональная, то  . В этом случае дисперсия групповых средних равна общей дисперсии ((
. В этом случае дисперсия групповых средних равна общей дисперсии ((  т.е. не будет внутригрупповой дисперсии. Это означает, что группировочный признак полностью определяет вариацию изучаемого признака, а влияние прочих факторных признаков равно нулю. При
т.е. не будет внутригрупповой дисперсии. Это означает, что группировочный признак полностью определяет вариацию изучаемого признака, а влияние прочих факторных признаков равно нулю. При 
 кг
кг кг.
кг.


 .
.
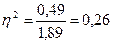 или 26 %.
или 26 %. .
.