 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Основные свойства средней арифметической
1. Произведение средней величины на сумму частот равно сумме произведений отдельных значений признака на соответствующие им частоты:
Используя данные таблицы, получим следующее равенство:
2. При уменьшении или увеличении частот каждого значения признака х в А раз величина средней арифметической не меняется:
Так, в нашем примере было бы удобнее рассчитывать среднюю, предварительно поделив все веса на 100:
Данное правило дает, таким образом, возможность: 1. Выражать многозначные числа частот в более компактных единицах измерения. 2. Заменять конкретные значения частот удельными весами, тогда:
если d выражена в %, или
если d представлена в долях единицы
3. Если каждое индивидуальное значение признака умножить или разделить на постоянное число А, то и среднее значение увеличится или уменьшится во столько же раз.
Предположим, что курс продажи в каждом случае возрастает в 1,2 раза, тогда и средний курс возрастет в 1,2 раза.
4. Если к каждому индивидуальному значению прибавить или из каждого значения вычесть постоянное число А, то и средняя величина возрастет или уменьшится на это же число А:
Используя это правило, вычтем из значений курса акций 100 рублей. Тогда:
5. Сумма отклонений индивидуальных значений признака от его среднего значения равна нулю:
Тогда для нашего примера:
Средняя гармоническая имеет более сложную конструкцию, чем средняя арифметическая. Среднюю гармоническую чаще всего применяют для расчетов тогда, когда в качестве весов используются не единицы совокупности – носители признака, а произведения этих единиц на значения признака (т.е. М= X · f). Например, есть данные о реализации продукта одного вида на трех рынках города:
Требуется рассчитать среднюю цену, по которой продавался товар. При расчете средней цены на один и тот же товар, который продается в трех разных торговых точках, необходимо выручку от реализации продукции поделить на количество реализованной продукции. Предположим, мы располагаем только данными о ценах на трех рынках и о количестве товара, проданного на каждом из них. При этом цены на отдельных рынках выступают в качестве вариантов, а количество проданного товара – в качестве весов. Тогда средняя цена определится по средней арифметической взвешенной, то есть:
Теперь предположим, что количество проданного товара неизвестно, а известны лишь цены и выручка от продажи. В этом случае логические рассуждения остаются теми же, но расчет следует записать в форме средней гармонической взвешенной. Чтобы исчислить среднюю, обозначим x·f=M, откуда f=M/x. Преобразуем формулу средней арифметической так, чтобы по имеющимся данным x и M можно было исчислить среднюю. В формулу средней арифметической взвешенной вместо x·f подставим M, вместо f – отношение M/x и получим формулу средней гармонической взвешенной:
Результат, как и следовало ожидать, получился тот же. Рассмотрим еще один пример расчета средней гармонической взвешенной. Допустим, в результате проверки двух партий муки потребителям установлено, что в первой партии муки высшего сорта было 3942 кг., что составляет 70,4 % общего веса муки этой партии. Во второй партии муки высшего сорта было 6520 кг, что составляет 78,6 % общего веса муки этой партии. Необходимо определить процент муки высшего сорта в среднем по первой и второй партиям вместе. Средний процент муки высшего сорта по двум партиям определяем по формуле средней гармонической взвешенной:
В том случае, если объемы явлений, т.е. произведения, по каждому признаку равны, применяется средняя гармоническая простая. К средней гармонической простой следует прибегать в случаях определения, например, средние затраты труда, времени, материалов на единицу продукции, не одну деталь по двум (трем, четырем и т.д.) предприятиям, рабочим, занятым изготовлением одного и того же вида продукции, одной и той же детали, изделия. Например, две автомашины прошли один и тот же путь: одна со скоростью 60 км/ч, а вторая – 80 км/ч. Тогда средняя скорость составит:
Таким образом,
где Cредняя геометрическая – это величина, применяемая для расчета средних из относительных величин. Поэтому средняя геометрическая используется в расчетах средних темпов роста. Формула средней геометрической выглядит следующим образом:
где x – цепной коэффициент роста (варьирующий признак); n – количество периодов, по которым имеются коэффициенты роста. Предположим, имеются следующие данные о тепах роста товарооборота фирмы за ряд лет.
Определим средние темпы роста с 2000 по 2003 годы. Значение темпов роста переводим из процентов в коэффициенты и подставляем в формулу средней геометрической.
Таким образом, средние темпы роста товарооборота фирмы составляют 1,063 или 106,3 % в год. Среднегодовые темпы роста могут рассчитываться с использованием другой формулы средней геометрической:
где у1 – абсолютная величина явления в первом году периода; уn – абсолютная величина явления в последнем году периода; n – количество лет периода.
Пример. Стоимость продукции, произведенной фирмой Х в 1991 г., составила 200000 долл., а в 1999 г. – 1200000 долл. Определим средние ежегодные (среднегодовые) темпы роста выпуска продукции фирмой Х:
Следовательно, средние ежегодные темпы роста составляли 1,251 или 125,1 %. Удобство данной формулы состоит в том, что при расчетах не требуются данные за все годы периода. Решение о том, какая из двух приведенных формул средней геометрической должна использоваться в каждом конкретном случае, принимается в зависимости от наличия исходных данных. Применение средней геометрической справедливо, если годовые коэффициенты роста за последующие годы составляют непрерывно возрастающий (или непрерывно убывающий) ряд. В случае же, когда среди данных имеются показатели роста как больше, так и меньше 1, расчет приобретает условный характер, и это надо специально оговаривать.
|








 ,
, ,
, .
. .
. руб.
руб. .
. руб.
руб. руб.
руб.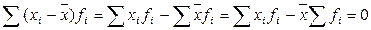 .
. .
. =
= 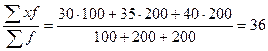 руб.
руб. ,
, руб.
руб. или 75,3 %.
или 75,3 %. км/ч.
км/ч. ,
, - сумма обратных значений вариант, n – число вариант.
- сумма обратных значений вариант, n – число вариант. ,
,
 ,
,