 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Основные теоретические положения
Основные теоретические положения. Закон Ома Участок ветви, содержащий один или несколько источников энергии, является активным. Рассмотрим участок электрической цепи (рис. 1.1).
При решении задач по теории электрических цепей выбирают положительное направление тока, которое указывается стрелкой. Направление тока характеризуется знаком тока. Понятия положительный или отрицательный участок имеют смысл, если сравнивать направление тока в проводнике с некоторым заранее выбранным направлением – так называемым положительным направлением тока. Запомнить! 1) Ток в сопротивлении всегда направлен от более высокого потенциала к более низкому, т.е потенциал падает по направлению тока (на рис. 1.1 условно точке «а» присвоим знак «+», а точке «с» – знак «–»). 2) Э.Д.С., направленная от точки «c» к точке «d», повышает потенциал последней на величину 3) Напряжение При обозначении напряжения (разности потенциалов) на схемах посредством стрелки она направляется от точки высшего потенциала к точке низшего потенциала. На рис. 1.1 ток протекает от точки «a» к точке «c», значит, потенциал На участке «c - d» Э.Д.С. Потенциал точки «b» равен:
Знак «–» перед Э.Д.С., совпадающей по направлению с током, объясняется следующим образом: напряжение на участке с Э.Д.С. противоположно направлено самой Э.Д.С. и определяемому напряжению. Напряжение
Ток на участке ab определяют по выражению
Формула (1.2) выражает обобщенный закон Ома, или закон Ома для активного участка цепи. Из формулы видно, что если ток, напряжение и Э.Д.С. совпадают по направлению, то в выражение закона Ома они входят с одинаковыми знаками. Если Э.Д.С. действует в сторону, противоположную положительному направлению тока, в выражении ставится знак «–». Закон Ома применяется как для участка ветви, так и для одноконтурной замкнутой схемы.
Пример 1.1
Пример 1.2
Подставим численные значения, получим:
Ответ:
Метод узловых напряжений Основные теоретические положения
Метод узловых напряжений заключается в определении на основании первого закона Кирхгофа потенциалов в узлах электрической цепи относительно некоторого базисного узла. Базисный узел в общем случае выбирается произвольно, потенциал этого узла принимается равным нулю. Разность потенциалов рассматриваемого и базисного узлов называется узловым напряжением. Положительное направление узловых напряжений указывается стрелкой от рассматриваемого узла к базисному. Число уравнений, составляемое по методу узловых напряжений, равно
где Для произвольной схемы, содержащей
где
Собственная проводимость узла равна сумме проводимостей ветвей, сходящихся в данном узле. Взаимная проводимость равна сумме проводимостей ветвей, соединяющих данные узлы. Выражение, стоящее в правой части уравнений системы, называют «узловой ток». Узловой ток (теоретическое понятие) – это алгебраическая сумма произведений Из системы (4.2) видно, что собственные проводимости входят в уравнения со знаком «+», а взаимные проводимости – со знаком «–». Алгоритм расчета электрических цепей по методу узловых напряжений: 1) Выбираем базисный узел. Желательно нулевой потенциал присвоить тому узлу, где сходится большее количество ветвей. Запомнить! Если в составе цепи имеется одна или несколько ветвей, содержащих идеальные Э.Д.С. (сопротивление таких ветвей равно нулю), то за базисный принимают один из узлов, между которыми находится ветвь с идеальной Э.Д.С. 2) Составляется система уравнений для неизвестных узловых напряжений в соответствии с общей структурой этих уравнений (4.2). 3) Решая данную систему, находят напряжения узлов относительно базиса. 4) Токи ветвей определяют по обобщенному закону Ома:
Частным случаем метода узловых напряжений является метод двух узлов. Если схема содержит только два узла, то в соответствие с методом узловых напряжений (в отсутствие идеальных Э.Д.С.) составляется только одно уравнение:
|




 (на рис. 1.1 условно зажиму Э.Д.С., подключенному к точке «c», присвоим знак «–», а зажиму, подключенному к точке «d» – знак «+»).
(на рис. 1.1 условно зажиму Э.Д.С., подключенному к точке «c», присвоим знак «–», а зажиму, подключенному к точке «d» – знак «+»). положительно, когда потенциал точки «a» выше, чем потенциал точки «c».
положительно, когда потенциал точки «a» выше, чем потенциал точки «c». будет меньше
будет меньше  на величину падения напряжения на сопротивлении
на величину падения напряжения на сопротивлении  , которое по закону Ома равно
, которое по закону Ома равно  :
:  .
.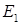 действует в сторону повышения потенциала, следовательно,
действует в сторону повышения потенциала, следовательно, 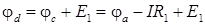 .
. .
. найдем как разность потенциалов:
найдем как разность потенциалов: .
. .
. Рис. 1.3
Рис. 1.3 если
если  ;
;  ;
;  ;
;  ;
;  ;
;  . Решение Запишем формулу для расчета напряжения между узлом «b» и узлом «a»
. Решение Запишем формулу для расчета напряжения между узлом «b» и узлом «a»  , Подставим численные значения, получим:
, Подставим численные значения, получим:  . Ответ:
. Ответ: 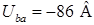 .
. 
 и
и  , если
, если  ;
;  ;
;  ;
;  ;
;  ;
;  ;
; 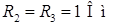 ;
;  ;
;  ;
;  ;
; 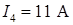 . Решение Используя обобщенный закон Ома для участка цепи, запишем формулы для определения напряжений
. Решение Используя обобщенный закон Ома для участка цепи, запишем формулы для определения напряжений 
 .
. ;
; .
. ,
,  .
.
 – количество узлов цепи,
– количество узлов цепи,  – количество идеальных источников Э.Д.С.
– количество идеальных источников Э.Д.С. узлов, система уравнений по методу узловых напряжений имеет вид:
узлов, система уравнений по методу узловых напряжений имеет вид:
 – собственная проводимость узла
– собственная проводимость узла  .
. – взаимная проводимость ветви, соединяющей узлы
– взаимная проводимость ветви, соединяющей узлы  .
.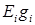 и
и  источника тока (если они есть) всех ветвей, примыкающих к рассматриваемому узлу. Слагаемое входит в выражение со знаком «+», если Э.Д.С. и источник тока направлены к узлу. В противном случае – ставится знак «–».
источника тока (если они есть) всех ветвей, примыкающих к рассматриваемому узлу. Слагаемое входит в выражение со знаком «+», если Э.Д.С. и источник тока направлены к узлу. В противном случае – ставится знак «–». .
. .
.