 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Параллельный колебательный контур и его свойства
Параллельным колебательным контуром называется двухполюсная электрическая цепь, подключенная к источнику гармонического сигнала и содержащая в своем составе резистор, конденсатор и индуктивность, соединенные параллельно (рис. 3.11). Резистор в контур может специально не включаться, но в контуре он всегда будет присутствовать, отражая потери, имеющие место в реальных реактивных элементах. Комплексная проводимость параллельного контура определяется следующими соотношениями
Изобразим для параллельного колебательного контура график зависимости реактивной проводимости Y от частоты (рис. 3.12), учитывая, что
Рис. 3.11. Параллельный колебательный контур
Анализ графика показывает, что на частоте ω0 реактивная проводимость контура становиться равной нулю. Это свидетельствует о том, что сопротивление цепи становиться чисто резистивным (активным) и сдвиг фаз между напряжением и током в контуре равен нулю. Следовательно, в параллельном контуре также имеет место явление электрического резонанса. Резонансная частота параллельного контура определяется той же формулой что и резонансная частотота последовательного контура
В диапазоне частот, когда частота источника сигнала меньше резонансной частоты f<f0 , преобладает реактивное сопротивление индуктивности, сопротивление контура имеет активно - индуктивный характер и фазовый сдвиг между напряжением и током есть величина положительная.
Рис. 3.12. График зависимости реактивной проводимости параллельного контура от частты
В области частот f>f0 преобладает реактивное сопротивление конденсатора, сопротивление контура активно – емкостное, ток источника опережает по фазе напряжение на выводах. Если рассмотреть, что происходит в параллельном контуре с энергией, то можно установить, что и при параллельном соединении реактивных элементов на резонансной частоте происходит непрерывный периодический процесс обмена энергиями между электрическим полем конденсатора и магнитным полем индуктивности, который сопровождается необратимыми потерями части энергии на резисторе. Энергия, поступающая от источника электрической энергии в контур, компенсирует тепловые потери на сопротивлении контура. Контур оценивается добротностью, показывающей отношение (с учетом 2π) величин энергий, накапливаемых на резонансной частоте в реактивных элементах параллельного контура к энергии, расходуемой в цепи в виде необратимых потерь, за период. Добротность параллельного контура определяется формулой
Следует иметь в виду, что, величины R, входящие в формулу добротности в параллельном (3.36) и последовательном (3.27, 3.28) контуре, существенно различны. Если не включать в контур дополнительный резистор, а учитывать только потери реактивных элементов, величины R в формулах добротности последовательного и параллельного контуров будут различаться на несколько порядков. При последовательном соединении L и C величина R = r, определяясь сопротивлением провода катушки r, будет составлять несколько десятков Ом. В параллельном контуре потери на тепловыделение за счет нагревания провода пересчитывают по формуле R =ρ2 /r, поэтому его величина десятки кОм. Отметим, что величина добротности параллельных контуров в зависимости от качества конденсатора и катушки индуктивности составляет Q =50 – 120. Поскольку реактивные проводимости на резонансной частоте равны и на них одно и тоже напряжение, то амплитуды токов на реактивных элементах контура равны ImL = ImC . К тому же,
Следовательно, на резонансной частоте амплитуды токов на реактивных элементах в Q раз превышают амплитуду тока, поданного на контур от источника. Комплексное сопротивление параллельного контура, если его выразить через добротность, равно
Тогда полное сопротивление цепи равно
График зависимости полного сопротивления параллельного контура от частоты показан на рис.3.13.
Рис. 3.13. График зависимости полного сопротивления параллельного контура от частоты
Полное сопротивление контура на резонансной частоте максимально и равно сопротивлению R. С отклонением от резонансной частоты (с увеличением расстройки относительно резонансной частоты) полное сопротивление контура уменьшается. Если параллельный контур подключить к реальному источнику гармонического тока, то можно утверждать, что параллельный контур «выделяет» напряжение резонансной частоты, а также сигналы, частоты которых находятся в полосе (диапазоне) частот примыкающей к резонансной частоте. Этот диапазон частот называют полосой пропускания контура. Границы полосы пропускания определяют частоты f1 и f2. Полоса пропускания контура определяется формулой
Резюмируя сказанное отметим, что параллельный колебательный контур обладает следующими свойствами. 1. В контуре наблюдается явление электрического резонанса. Поскольку ток на реактивных элементах увеличиваются в Q раз по сравнению с током источника, то правильнее говорить, что в контуре имеет место явление электрического резонанса токов. 2. В случае высокой добротности контура явление резонанса характеризуется тем, что контур мало энергии потребляет от источника, а внутри него идет непрерывно периодический процесс обмена энергиями реактивных элементов. Контур как бы становиться генератором гармонической ЭДС. 3. Ток на реактивных элементах может почти в 100 раз (точнее в Q раз) превышать ток источника. 4. Если источник гармонического тока вырабатывает сигналы с несколькими частотами, то параллельный контур выделяет сигналы, частоты которых лежат в его полосе пропускания. Выделение сигналов будет тем лучше, чем больше величина добротности контура. Это свойство можно использовать для выделения полезных сигналов, например в радиовещательном приемнике. 5. Сопротивление параллельного контура на резонансной частоте максимально. Для обеспечения передачи энергии от источника в нагрузку параллельный контур, при работе на резонансной частоте, должен подключаться к реальному источнику тока, обладающему большим внутренним сопротивлением. При малых величинах внутренних сопротивлений источника добротность контура существенно уменьшается.
|



 (3.33)
(3.33) (3.34)
(3.34)
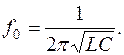 (3.35)
(3.35)

 (3.36)
(3.36) (3.37)
(3.37) (3.38)
(3.38) (3.39)
(3.39) (3.40)
(3.40)

 (3.41)
(3.41)