 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Средства и способы проведения эксперимента
Лабораторная работа № 6 Измерение характеристик и параметров сложных электрических цепей
Цели работы 1. Углубить и закрепить знания о понятиях, параметрах и характеристиках, которыми пользуются при описании сложных электрических цепей. 2. Сформировать практические умения математической записи, определения различными методами тока и напряжения на элементах сложной цепи, амплитудно-частотных и фазо–частотных, передаточных, импульсных характеристик для типовых звеньев электрической цепи, а также измерений их параметров с помощью контрольно-измерительной аппаратуры. 3. Выработать умения практической работы с моделирующей программой (программным эмулятором) ELECTRONICS WORKBENCH, необходимые для оценки параметров и характеристик сложных электрических цепей. 4. Выработать умения практической работы с системой MATLAB, необходимые для для оценки параметров и характеристик сложных электрических цепей. Самостоятельная работа студентов Перед выполнением лабораторной работы студенту необходимо. 1. Изучить теорию, которой пользуются в электротехнике для описания, оценки и расчетов сложных электрических цепей, понятия, которыми характеризуют сложные электрические цепи. 2. Провести самопроверку эффективности своей теоретической подготовки, ответив на вопросы, приведенные в разделе «Контрольные вопросы». 3. Изучить средства и способы проведения эксперимента, краткие описания измерительных приборов и методов измерений, используемых в работе. В результате исполнения этого пункта студент должен уметь объяснять порядок выполнения работы и то, какие результаты он ожидает получить. 4. Подготовить отчет о лабораторной работе. В тетради изобразить принципиальные схемы экспериментов. В тетради подготовить таблицы, в которые будут записываться данные, полученные в результате проведения экспериментов. Подготовить оси координат графиков, необходимых для изображения исследуемых сигналов или осциллограм. Выполняя предыдущее надо помнить, что схемы, таблицы, результаты исследований помещаются в тетради отдельно по каждому пункту задания, желательно на отдельных страницах отчета. Для заданной преподавателем схемы электрической цепи определить характер входного сопротивления схемы. Пользуясь понятием о делителе напряжения для заданной преподавателем схемы электрической цепи рассчитать комплексную амплитуду напряжения на конденсаторе. Пользуясь понятием о делителе тока для заданной преподавателем схемы электрической цепи рассчитать комплексную амплитуду напряжения на резисторе. Для заданной преподавателем схемы электрической цепи методом контурных токов рассчитать комплексные амплитуды всех токов и напряжений. Для заданной преподавателем схемы электрической цепи методом узловых напряжений рассчитать комплексные амплитуды всех токов и напряжений. Определить амплитуды и начальные фазы всех токов и напряжений. Построить векторные диаграммы токов и напряжений для всех элементов схемы. Для заданной преподавателем схемы электрической цепи рассчитать операторную передаточную характеристику. Для этой цепи построить диаграмму нулей и полюсов, АЧХ, ФЧХ, переходную и импульсную характеристики.
Средства и способы проведения эксперимента Лабораторная работа вначале выполняется на IBM PC с использованием моделирующей элементы и устройства электрической цепи программы (программного эмулятора) ELECTRONICS WORKBENCH. В данной лабораторной работе для проведения экспериментов, используются амперметр и вольметр, позволяющие измерять напряжение, силу тока. Пиктограммы приборов («иконки») показаны на рис. 3.16 слева вверху. Для визуального наблюдения графиков зависимостей напряжения от частоты – амплитудно-частотной характеристики (АЧХ) и фазы от частоты – фазо-частотной характеристики (ФЧХ) используется измеритель частотных характеристик (Bode Plotter). Иконка прибора и развернутое, более крупное его изображение, показаны на рис. 3.16. Для получения развернутого изображения прибора необходимо навести указатель мыши на иконку прибора и дважды щелкнуть левой кнопкой мыши. На иконке прибора показаны входные клеммы (порт входа – IN) и выходные (порт выхода –OUT). На экране измерителя частотных характеристик имеются оси координат и перемещающаяся в любое место экрана специальная визирная линейка. Переместив указатель мыши на линейку и, удерживая нажатой левую кнопку мыши, устанавливается требуемое значение амплитуды (фазы), как точка пересечения визирной линейки и графика u = F(f) или φ = F(f). Расположенные справа экрана цифровые дисплеи покажут значения амплитуды (фазы) и частоты для выбранной точки.
Рис. 3.16. Пример изображения «окна» Electronics Workbench вольтметром, амперметром и измерителем АЧХ и ФЧХ.
При работе с измерителем частотных характеристик требуется задавать масштаб по оси ординат и абсцисс графика. При нажатии кнопки «LIN» устанавливается линейный масштаб, при нажатии «LOG» -логарифмический. Выбор наблюдаемой АЧХ или ФЧХ производится кнопками « Magnitude» и «Phase». О средствах системы MATLAB будет рассказано в эксперименте 5.
Порядок выполнения работы Эксперимент 1. Иcследование свойств делителя напряжения. Для проведения эксперимента необходимо выполнить следующую последовательность действий. 1. Открыть диалоговое окно программы «Electronics Workbench». При появлении сообщения «Could not open file» нажмите кнопку «ОК». 2. Откройте необходимый файл, нажав, например, кнопку «открыть», и, выбрав необходимое в контекстном меню, открыть файл lr3-1. 3. На экране монитора появиться схема установки для эксперимента(рис. 3.17). Она содержит три резистора и три вольтметра. Резистор величиной 4.8 кОм может подключаться или отключаться нажатием клавиши «пробел» на клавиатуре. При этом должен быть установлен английский алфавит.
Рис. 3.17. Схема для исследования свойств делителя напряжения.
4.Запустить моделирующую программу, наведя указатель курсора на расположенную в правом верхнем углу пиктограмму включателя/выключателя I/O и щелкнув левой кнопкой мыши. 5. Произвести отсчет c дисплеев приборов (рис.3.18) величин напряжений на элементах делителя для разных сопротивлений (in– включить, off– выключить). Записать величины напряжений в таблицу 3.1.
Таблица 3.1. Результаты измерений
Рис. 3.18. Измерение напряжений на элементах делителя.
6. Перевести кнопку I/O в положение O. Рассчитать теоретические величины напряжений, какие должны показывать вольтметры. Сделать выводы о свойствах делителя напряжения.
Эксперимент 2. Иcследование свойств делителя тока. Для проведения эксперимента необходимо: 1. Используя команды «Файл. Открыть», выбрав в контекстном меню необходимое и нажав кнопку «ОК» открыть файл lr3-2. На вопрос о сохранении изменений в файле lr3-1 дать отрицательный ответ. 2. На экране монитора появится схема установки для эксперимента (рис. 3.19). Она содержит 4 амперметра, три резистора и два ключа. 3.Запустить моделирующую программу, наведя указатель курсора на расположенную в правом верхнем углу пиктограмму включателя/выключателя I/O и щелкнув левой кнопкой мыши. 4. Произвести отсчет c дисплеев приборов величин токов, протекающих через элементы для разных сопротивлений делителя (in– включить, off – выключить). Записать величины напряжений в таблицу 3.2.
Рис. 3.19 Схема для исследования свойств делителя тока.
Таблица 3.2. Результаты измерений.
5. Перевести кнопку I/O в положение O. Рассчитать теоретические величины токов, которые должны показывать амперметры. Сделать выводы о свойствах делителя тока.
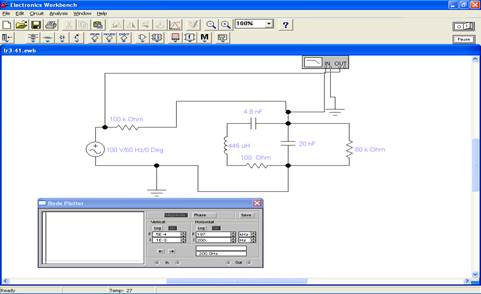
Эксперимент 3. Измерение параметров АЧХ и ФЧХ параллельного контура. Для проведения эксперимента необходимо выполнить следующую последовательность действий. 1. Используя команды «Файл. Открыть», выбрав в контекстном меню необходимое и нажав кнопку «ОК» открыть файл lr3-3. На вопрос о сохранении изменений в файле lr3-2 дать отрицательный ответ. 2. На экране монитора появится схема установки для эксперимента (рис. 3.20). Она содержит параллельный контур, измеритель частотных характеристик и вспомогательные элементы для измерения АЧХ и ФЧХ.
Рис. 3.20. Схема для исследования параметров АЧХ и ФЧХ параллельного контура.
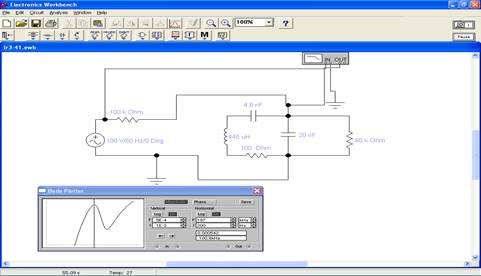
3.Запустить моделирующую программу, наведя указатель курсора на расположенную в правом верхнем углу пиктограмму включателя/выключателя I/O и щелкнув левой кнопкой мыши. 4. Просмотреть, что представляет собой графики АЧХ и ФЧХ параллельного контура. Определить соответствуют ли они теоретическим зависимостям, имеет ли место явление резонанса токов. Используя визирную линейку определить резонансную частоту f0 параллельного контура (рис.3.21). Значение резонансной частоты записать в таблицу. 5. Сдвигая визирную линейку влево и вправо, измерить частоты fЛ и fП , на которых АЧХ уменьшается в 1.4 раза. Частоты fЛ и fП записать в таблицу. Рассчитать полосу пропускания контура и его добротность; результаты занести в таблицу 3.3.
Рис. 3.21. Определение резонансной частоты параллельного контура. Таблица 3.3. Результаты измерений.
6. Сделать выводы о свойствах параллельного контура.
Эксперимент 4. Измерение частотных характеристик кварцевого пьезорезонатора. Для проведения эксперимента необходимо выполнить следующую последовательность действий. 1. Используя команды «Файл. Открыть», выбрав в контекстном меню необходимое и нажав кнопку «ОК» открыть файл lr3-4. На вопрос о сохранении изменений в файле lr3-3 дать отрицательный ответ.
Рис. 3.22. Схема измерения частотных характеристик кварцевого пьезорезонатора.
Рис. 3.23. Определение резонансной частоты кварцевого пьезорезонатора.
2. На экране монитора появится схема установки для эксперимента (рис. 3.22). Она содержит представленный схемой замещения кварцевый пьезорезонатор, а также измеритель частотных характеристик и вспомогательные элементы для измерения АЧХ и ФЧХ. 3.Запустить моделирующую программу, наведя указатель курсора на пиктограмму I/O и щелкнув левой кнопкой мыши. 4. Просмотреть, что представляют собой графики АЧХ и ФЧХ кварцевого пьезорезонатора. Определить соответствуют ли они теоретическим зависимостям. Используя визирную линейку определить и записать в отчет величины частот параллельного и последовательного резонанса (рис. 3.23). 5. Сделать выводы о частотных свойствах кварцевого пьезорезонатора.
Эксперимент 5. Измерение частотных характеристик ЦТС –(PZT-) керамического пьезорезонатора. Для проведения эксперимента необходимо выполнить: 1. Используя команды «Файл. Открыть», выбрав в контекстном меню необходимое и нажав кнопку «ОК» открыть файл lr3-5. На вопрос о сохранении изменений в файле lr3-4 дать отрицательный ответ. 2. На экране монитора появится схема установки для эксперимента (рис. 3.24). Она содержит представленный схемой замещения ЦТС –(PZT-) керамический пьезорезонатор, а также измеритель частотных характеристик и вспомогательные элементы для измерения АЧХ и ФЧХ.
Рис. 3.24. Схема измерения частотных характеристик ЦТС –(PZT-) керамического пьезорезонатора. 3.Запустить моделирующую программу, наведя указатель курсора на расположенную в правом верхнем углу пиктограмму включателя/выключателя I/O и щелкнув левой кнопкой мыши. 4. Просмотреть, что представляют собой графики АЧХ и ФЧХ ЦТС –(PZT-) керамического пьезорезонатора. Определить соответствуют ли они теоретическим зависимостям. Используя визирную линейку определить и записать в отчет величины частот параллельного и последовательного резонанса (рис.3.25).
Рис. 3.25. Определение резонансной частоты ЦТС –(PZT-) керамического пьезорезонатора.
5. Сделать выводы о частотных свойствах ЦТС –(PZT-) керамического пьезорезонатора.
Эксперимент 6. Измерение и анализ характеристик сложной электрической цепи. Для выполнения задания необходимо выполнить следующие операции: 1. Закрыть ELECTRONICS WORKBENCH. Запустить из главного меню операционной системы Windows MATLAB. Для запуска MATLAB, как обычно, необходимо дважды щелкнуть по специфической иконке с надписью. 2. После запуска системы MATLAB на экране появится основное окно пользовательского интерфейса в открытом виде как на рис.3.26.
Рис. 3.26. Пример изображения «окна» MATLAB после загрузки.
Рис. 3.27. Изображение окна интерактивной системы для исследования RLC цепей.
3. Набрать в командной строке >>rlcdemo (малыми буквами – RLCDEMO). Через некоторое время откроется окно интерактивной системы для исследования RLC цепей, показанное на рис. 3.27. С его помощью можно провести исследование семи Г-образных RLC схем с различными вариантами исполнения продольного и поперечного элементов. Схема соединения элементов выбирается в строках меню (SYSTEM, TOPOLOGY). При этом в диалоговом окне системы отображаются АЧХ и ФЧХ цепи (BODE DIAGRAM), переходная характеристика (STEP RESPONSE), диаграмма полюсов и нулей (POLE – ZERO MAP) и диаграмма Найквиста. Параметры выбранной RLC цепи задаются в разделе SYSTEM PARAMETRS ползунковыми движками. Кроме того, под каждой схемой приведены выражения для операторной передаточной характеристики. Для проведения эксперимента необходимо выполнить следующую последовательность действий. 1. Выбрать исследуемую Г- образную схему и записать ее функциональное назначение. 2. При среднем положении ползунков зарисовать для выбранной схемы графики АЧХ и ФЧХ цепи (BODE DIAGRAM), переходной характеристики (STEP RESPONSE) и диаграмму (POLE – ZERO MAP). Описать словесно расположение полюсов и нулей и на этом основании дать характеристику цепи с точки зрения ее устойчивости, резонансных свойств. Выявить связь между параметрами АЧХ и ФЧХ цепи (BODE DIAGRAM) и переходной характеристикой (STEP RESPONSE). 3. Варьируя величинами R, L, C установите связь между значениями R, L, C и положением нулей и полюсов. Отразите пунктирными линиями направление перемещения нулей и полюсов. 4. Варьируя величинами R, L, C установите связь между значениями R, L, C и формой АЧХ. Отразите штриховыми линиями изменения графиков. 5. Варьируя величинами R, L, C установите связь между значениями R, L, C и формой переходной характеристики. Отразите штриховыми линиями изменения графиков. Для понимания происходящих изменений целесообразно представлять, какими величинами определяются коэффициенты полиномов числителя и знаменателя передаточной операторной характеристики. Решение:
>> rlcdemo
Transfer function: s ----------- s^2 + s + 1
Eigenvalue Damping Freq. (rad/s)
-2.50e-002 + 1.00e+000i 2.50e-002 1.00e+000 -2.50e-002 - 1.00e+000i 2.50e-002 1.00e+000 3.2.5. Последовательный колебательный контур и его свойства Последовательным колебательным контуром называется двухполюсная электрическая цепь, подключенная к источнику гармонического сигнала и содержащая в своем составе резистор, конденсатор и индуктивность, соединенные последовательно (рис. 3.8).
Рис. 3.8. Последовательный колебательный контур
Резистор может в контур может специально не включаться, но в контуре он всегда будет присутствовать, отражая потери, имеющие место в реальных реактивных элементах. Комплексное сопротивление последовательного контура определяется следующими соотношениями
Изобразим для последовательного колебательного контура график зависимости реактивного сопротивления Х от частоты (рис.3.9), учитывая, что
Анализ графика показывает, что на частоте ω0 реактивное сопротивление контура X становиться равным нулю. Это свидетельствует о том, что сопротивление цепи становиться чисто резистивным (активным) и сдвиг фаз между напряжением и током в контуре равен нулю. Явление в электрической цепи, содержащей индуктивность и емкость, при котором сдвиг фаз между напряжением и током равен нулю, называется электрическим резонансом. Частота, на которой наблюдается данное явление, получило название резонансной частоты.
Рис. 3.9. График зависимости реактивного сопротивления от частоты
Резонансную угловую частоту ω0, как скорость изменения полной фазы, можно определить из
Соответственно, резонансная частота f0 равна
В диапазоне частот, когда частота источника сигнала меньше резонансной частоты f<f0 , преобладает реактивное сопротивление емкости, сопротивление контура имеет активно-емкостной характер и фазовый сдвиг между напряжением и током есть величина отрицательная. В области частот f>f0 преобладает реактивное сопротивление индуктивности, сопротивление контура активно-индуктивное, напряжение на выводах цепи опережает по фазе ток. Для более детальной характеристики явления резонанса рассмотрим процессы обмена энергией, которые происходят в последовательном контуре. Если исходить из (2.29) и (2.37) а также из того, что через реактивные элементы протекает ток одинаковой амплитуды, то можно показать, что на резонансной частоте средние значения энергий емкости и индуктивности одинаковы, а их сумма является величиной постоянной, не зависящей от времени. Это свидетельствует о том, что энергия, которую первоначально (при подключении) накопили емкость и индуктивность в своих электрических и магнитных полях в последующем только перераспределяется между ними или, другими словами, перекачивается из емкости в индуктивность и обратно, причем уже без участия в этом процессе источника энергии. В идеале, если бы при этом исключить резистор и потери в реактивных элементах, то источник можно было бы вообще отключить и, несмотря на это, в последовательном колебательном контуре все равно бы протекал непрерывный периодический процесс обмена энергией между электрическим полем емкости и магнитным полем индуктивности. В реальном последовательном контуре из-за сопротивления часть энергии обменных процессов превращается в тепло, поэтому источник энергии все время восполняет необратимые потери энергии в сопротивлении. Отношение величин энергий, накапливаемых на резонансной частоте в реактивных элементах последовательного контура к энергии, расходуемой в цепи в виде необратимых потерь, за период, называется добротностью контура. Обычно при оценке величины добротности указанное отношение умножают на множитель 2π.
Из формул следует, что величина добротности помимо того, что характеризует соотношение энергий, отражает также во сколько раз реактивные сопротивления элементов контура больше активного сопротивления R. Отметим, что величина добротности последовательных контуров в зависимости от качества конденсатора и катушки индуктивности составляет Q = 50 – 120. Поскольку реактивные сопротивления на резонансной частоте равны и через них протекает один и тот же ток. то амплитуды напряжений на реактивных элементах контура равны UmL = UmC . К тому же,
Следовательно, на резонансной частоте амплитуды напряжений на реактивных элементах в Q раз превышают амплитуду напряжения, поданного на контур от источника. Комплексное сопротивление последовательного контура (3.23) можно выразить через добротность
Тогда полное сопротивление цепи равно
График зависимости полного сопротивления последовательного контура от частоты показан на рис. 3.10.
Рис. 3.10. График зависимости полного сопротивления последовательного контура от частоты Полное сопротивление контура на резонансной частоте минимально и равно сопротивлению R. Если последовательный контур подключить к реальному источнику гармонической ЭДС, то, исходя из правила простейшего делителя напряжения, можно утверждать, что последовательный контур подавляет («вырезает», осуществляет режекцию) напряжения резонансной частоты. Резюмируя сказанное отметим, что последовательный колебательный контур обладает следующими свойствами. 1. В контуре наблюдается явление электрического резонанса. Поскольку напряжения на реактивных элементах увеличиваются в Q раз по сравнению с напряжением источника, то правильнее говорить, что в контуре имеет место явление электрического резонанса напряжений. 2. В случае высокой добротности контура явление резонанса характеризуется тем, что контур мало энергии потребляет от источника, а внутри него идет непрерывно периодический процесс обмена энергиями реактивных элементов. Контур как бы становиться генератором гармонической ЭДС. 3. Напряжение на реактивных элементах может почти в 100 раз (точнее в Q раз) превышать напряжение источника. 4. Сопротивление контура на резонансной частоте минимально и практически равно нулю. Если источник гармонической ЭДС вырабатывает сигналы с несколькими частотами, то последовательный контур подавляет сигнал, частота которого совпадает с резонансной частотой. Режекция будет тем лучше, чем больше величина добротности контура. Это свойство можно использовать для подавления сигналов – помех. 5. Для обеспечения передачи энергии от источника в нагрузку контур, при работе на резонансной частоте, должен подключаться к реальному источнику ЭДС, обладающему малым внутренним сопротивлением.
|

















 (3.23)
(3.23) (3.24)
(3.24)

 (3.25)
(3.25) (3.26)
(3.26) (3.27)
(3.27) (3.28)
(3.28) (3.29)
(3.29) (3.30)
(3.30) (3.31)
(3.31) (3.32)
(3.32)
