ПОЗНАВАТЕЛЬНОЕ

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Динамическое рассеяние света

Определение размеров наночастиц в водных суспензиях

Методом динамического рассеяния света

Цель работы:

знакомство с возможностями анализатора размеров частиц Horiba LB-550 при оценке параметров ансамбля наночастиц, взвешенных в жидкости, в процессе изготовления и хранения различных суспензий.

Задачи, решаемые в процессе выполнения работы:

Освоить методику проведения измерений параметров исследуемых образцов водных суспензий наночастиц различного состава.
Освоить проведение расчетов основных параметров распределения наночастиц в исследуемом образце
Провести измерения параметров распределения наночастиц в исследуемых образцах и сравнить расчетные параметры (задание необходимо согласовать с преподавателем):

а) полученные в ходе последовательных измерений одного образца;

б) полученные при измерении параметров одного образца в различных состояниях;

в) полученные при измерениях разных образцов.

Сделать выводы о характере распределения по размерам параметров ансамбля наночастиц в исследуемых образцах и характере наблюдаемых в проведенном эксперименте изменениях.

В работе используется анализатор размеров частиц Horiba LB-550, принцип работы которого основан на динамическом рассеянии света.

Технические характеристики прибора Horiba LB-550

Ø Принцип измерения: основан на динамическом рассеянии света

Ø Диапазон размера частиц: он 1 нм до 6 мкм

Ø Количество пробной жидкости необходимой для измерения: от 2 мл до 4 мл

Ø Источник излучения: лазерный диод 650 нм, 5мВт

Динамическое рассеяние света

(фотонная корреляционная спектроскопия; квазиупругое рассеяние света)

Для измерения размеров наночастиц используется метод динамического рассеяния света (ДРС). Данный метод позволяет определить коэффициент диффузии наночастиц в жидкости путем анализа характерного времени флуктуаций интенсивности рассеянного света. Далее, из коэффициента диффузии рассчитывается радиус наночастиц.

Метод динамического рассеяния света используется также для измерения скоростей потоков жидкости и газа. Традиционно, этот вариант метода носит название лазерной доплеровской анемометрии (ЛДА).

В качестве примера рассмотрим диффузию монодисперсных наночастиц, взвешенных в жидкости. Хаотическое броуновское движение частиц вызывает микроскопические флуктуации их локальной концентрации. В свою очередь, эти флуктуации приводят к локальным неоднородностям показателя преломления среды. При прохождении лазерного луча через такую среду часть света будет рассеяна на этих неоднородностях. Флуктуации интенсивности рассеянного света будут соответствовать флуктуациям локальной концентрации дисперсных частиц. Информация о коэффициенте диффузии частиц содержится в зависящей от времени корреляционной функции флуктуаций интенсивности. Временная автокорреляционная функция согласно определению имеет следующий вид:

⁽¹⁾

где интенсивность I имеет различные значения во время t и (t-τ). t_m - это время интегрирования (время накопления корреляционной функции). Очевидно, что при τ = 0, автокорреляционная функция равна среднеквадратичной интенсивности <I²>. Для больших времен корреляция отсутствует, и автокорреляционная функция равна квадрату средней интенсивности рассеяния:

⁽²⁾

В соответствии с гипотезой Онзагера, релаксация микроскопических флуктуаций концентрации к равновесному состоянию может быть описана первым законом Фика (уравнением диффузии):

⁽³⁾

где c(r, t) - концентрация и D - коэффициент диффузии частиц. Можно показать, что автокорреляционная функция интенсивности экспоненциально затухает во времени и характерное время релаксации однозначно связано с D. Корреляционная функция интенсивности рассеянного света имеет вид:

⁽⁴⁾

где в соответствии с решением уравнения диффузии обратное время корреляции равно:

⁽⁵⁾

Волновой вектор флуктуаций концентрации описывается выражением:

⁽⁶⁾

В выражениях 4-6: a и b - экспериментальные константы, n- показатель преломления жидкости, в которой взвешены дисперсные частицы,λ - длина волны лазерного света и θ - угол рассеяния.

Рис. 1. Схема процесса рассеяния света

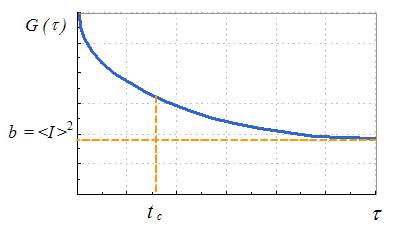
Рис. 2. Автокорреляционная функция рассеянного света

G(τ) –корреляционная функция интенсивности рассеянного света; t_c – обратное время корреляции;

b – экспериментальная константа;

Константы t_c, a и b могут быть найдены путем аппроксимации измеренной корреляционной функции теоретической экспоненциальной функцией. Если форма частиц известна или задана, их размер может быть рассчитан с использованием соответствующей формулы. Например, для сферических частиц можно использовать формулу Стокса-Эйнштейна:

⁽⁷⁾

где k_B - константа Больцмана, T - абсолютная температура и η - сдвиговая вязкость среды, в которой взвешены частицы радиуса R.

С помощью динамического рассеяния света может быть решена также задача измерения вязкости жидкости. Для случая рассеяния света на частицах известного размера, измеренное характерное время флуктуаций позволяет рассчитать вязкость жидкости.

Проблема аппроксимации экспериментальных данных проста для рассмотренного случая рассеяния света монодисперсными сферическими частицами. Для полидисперсных образцов интерпретация экспериментальных данных усложняется. Для реально достижимой точности измерений могут быть получены только два-три параметра полидисперсного распределения: средний размер частиц, ширина распределения и асимметрия распределения.