 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Проверка существования минимума функции 12
Тема 6.8. Лабораторная работа Методы многомерной оптимизации
Вопросы, подлежащие изучению
1.Постановка задачи многомерной оптимизации. 2.Классификация задачи оптимизации. 3.Основные понятия: выпуклое множество, целевая функция, линии уровня, поверхности уровня, градиент скалярной функции и его свойства, локальный и глобальный минимум, выпуклая функция, условия существования минимума функции нескольких переменных. 4.Градиентные методы и алгоритмы оптимизации: метод с дроблением шага; метод наискорейшего спуска аналитический; метод наискорейшего спуска численный. 5.Основные свойства градиентных методов оптимизации, различия методов. 6.Начальная точка траектории поиска минимума, свойства траектории, условия окончания процесса оптимизации.
Задание
1. Выбрать индивидуальное заданиеиз табл. 6.8-1 для решения задачи оптимизации функции нескольких переменных: · функцию – f(x, y); · метод оптимизации для «ручного расчета» – определяется значением параметра p; · метод оптимизации для «расчета на ПК» – значения параметровt и r. 2. Проверить условия существования точки минимумазаданной функции f(x). 3. Решить задачу многомерной оптимизации аналитическим методом. 4. Выбрать начальную точку x0, y0итерационного процесса оптимизации. 5. Решить задачу оптимизации « ручным расчетом»(3 итерации) выбранным методом. 6. Вычислить погрешности 7. Составить схему алгоритма, программу решения задачи оптимизации и провести контрольное тестирование. 8. Решить задачу многомерной оптимизации «расчетом на ПК» при точности определения минимума E=0.1, 0.05, 0.01, 0.001. 9. Построить траекторию поиска минимума по результатам «расчета на ПК» и изобразить схематически линии уровня, проходящие через точки траектории. На графике указать точку минимума, найденную в п.3 задания. 10. Решить задачу оптимизации спомощью математических пакетов.
Варианты задания Таблица 6.8-1
В табл. 6.8-1 р, t – номер метода решения задачи оптимизации: 1 – ГДШ; 2 – НСЧ;
Содержание отчета
1.Индивидуальное задание. 2.Результаты проверки условия существования точки минимума. 3.Аналитическое решение задачи оптимизации. 4.Начальная точка численного процесса оптимизации. 5.Результаты «ручного расчета» задачи оптимизации выбранными методами (3 итерации), представленные в табл. 6.8-2. Таблица 6.8-2
6.Значения погрешностей 7.Схемы алгоритмов и программы используемых численных методов оптимизации и результаты контрольного тестирования при точности вычисления минимума E = 0.1; 0.05; 0.01; 0.001.
8.Результаты решения задачи многомерной оптимизации «расчетом на ПК», представленные в табл. 6.8-3. Таблица 6.8-3
9.Траектория поиска минимума. 10.Результаты выполнения задания, полученные с помощью математических пакетов.
Пример выполнения задания
1. Задание для решения задачи многомерной оптимизации: · функция – · метод оптимизации для «ручного расчета» - значение параметра p=3; · метод оптимизации для расчета на ПК – значение параметра t=1.
Проверка существования минимума функции Из [2] известно, что всякий глобальный минимум выпуклой функции является одновременно и локальным. Проверить, что функция Матрица Гессе для функции
а угловые миноры:
Таким образом, функция 12 |








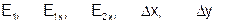 выбранных методов после
выбранных методов после


 ;
; ,
,
 .
. - выпуклая на множестве R.
- выпуклая на множестве R.