 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса - ваш вокал
Игровые автоматы с быстрым выводом
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший "Салат из свеклы с чесноком"
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
 Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
 Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
| Решение задачи Коши ОДУ с помощью математических пакетов
Для решения с использованием пакета Mathcad ОДУ 1-го порядка методом Эйлера необходимо задать начальные условия: x0, y0, шаг интегрирования – h и количество вычисляемых точек – n. Используемый в расчетах параметр i показывает номер итерации. Результаты, полученные по формулам метода Эйлера, выводятся в форме таблицы, где помимо приближенного решения (yi) получено точное решение (yi) и погрешности (yi - yti): Пакет MatLab включает несколько функций, реализующих различные методы решения задачи Коши для ОДУ. Синтаксически эти функции различаются лишь именами, способ обращения к ним одинаков. Так, например, в функции ode45( ) используется явный метод Рунге-Кутты 4-го и 5-го порядков. Если характеристики задачи неизвестны, рекомендуется первую попытку решения сделать с помощью этой функции. В функции ode23( ) используется явный метод Рунге-Кутты 2-го и 3-го порядков. В функции ode23t ( ) реализован неявный метод Рунге-Кутты с первым шагом по методу трапеции и вторым шагом по методу «дифференцирования назад» 2-го порядка. Простейшее обращение к любой функции ode***( ) имеет следующий вид: [xout, yout]=ode***(fun,xspan, y0), где: fun - указатель на функцию вычисления правых частей дифференциального уравнения; tspan - вектор, содержащий “контрольные значения” независимой переменной; y0- начальное значение зависимой переменной; xout - вектор-столбец контрольных значений независимой переменной; yout - решение, представленное массивом, в котором каждая строка соответствует одному элементу в столбце tout. Опишем функцию вычисления правых частей дифференциального уравнения | function dydx = fun(x,y) dydx = [y]; | Задав начальные условия, обратимся к функциям ode23( ) и ode45( ) | xspan=0:0.1:1 y0=[1]; options=odeset('InitialStep',0.1); [xout,yout]=ode23(@fun,xspan,y0); xout yout | xspan = 0.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000 0.9000 1.0000 | xout = 0.1000 0.2000 0.3000 0 .400 0.5000 0.6000 0.7000 0.8000 0.9000 0.0000 | yout = 1.0000 1.1052 1.2214 1.3498 1.4918 1.6487 1.8221 2.0137 2.2255 2.4595 2.7182 | | xspan=0:0.1:1 y0=[1]; options=odeset('InitialStep',0.1); [xout,yout]=ode45(@fun,xspan,y0); xout yout | xspan= 0.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000 0.9000 1.0000 | xout= 0.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000 0.9000 1.0000 | yout= 1.0000 1.1052 1.2214 1.3499 1.4918 1.6487 1.8221 2.0138 2.2255 2.4596 2.7183 |
6.5.6. Контрольные вопросы по теме
Методы решения дифференциальных уравнений
- Что такое обыкновенное дифференциальное уравнение?
- Что такое порядок ОДУ?
- Что называется аналитическим решением ОДУ 1-го порядка?
- Что является общим решением ОДУ
 ? ? - Что является геометрической интерпретацией общего решения ОДУ
 ? ? - Что является частным решением ОДУ
 ? ? - Что является численным решением ОДУ
 ? ? - Что относится к начальным условиям при решении ОДУ 1-го порядка численными методами?
- Имеет ли задача Коши для дифференциального уравнения 1-го порядка единственное решение?
- По какому правилу проводят оценку погрешности решения методов Рунге-Кутты?
- Как выглядит формула для определения очередного значения функции по методу Рунге-Кутты 1-го порядка?
- Уменьшение шага интегрирования при использовании методов Рунге-Кутты приводит к уменьшению или увеличению погрешности?
- В обыкновенном дифференциальном уравнении присутствуют производные разных порядков от одной переменной или только первая производная от нескольких переменных?
- Методы Рунге-Кутты являются одношаговыми или двухшаговыми методами?
- Сколько раз на каждом шаге необходимо вычислять
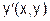 в модифицированном методе Эйлера? в модифицированном методе Эйлера? - Очередная точка решения ОДУ методом Рунге-Кутты вычисляется на основании одного или двух предыдущих значений функции?
- Возможно ли в методах Рунге-Кутты применение переменного шага интегрирования?
- Процесс решения дифференциального уравнения называется интегрированием или дифференцированием?
- Каковы формулы оценки погрешности методов Рунге-Кутты?
- Почему метод Эйлера называют методом Рунге-Кутты первого порядка?
- Модифицированный метод Эйлера относится к методам Рунге-Кутты решения ОДУ 1-го или 2-го порядка?
- Что требуется предварительно сделать, чтобы применить методы Рунге-Кутты при решении ОДУ 2-го порядка?
- С помощью чего при оценке погрешности метода автоматического выбора шага учитывается порядок используемого метода Рунге-Кутты?
- С помощью какого параметра происходит достижение заданной точности решения ОДУ в методе автоматического выбора шага?
- Можно ли оценить погрешность решения ОДУ,не зная точного решения?
- В каком методе решения ОДУподынтегральная функция на отрезке аппроксимируется интерполяционным многочленом 1-го порядка, а затем интегрируется методом прямоугольников?
- В каком методе решения ОДУ подынтегральная функция на отрезке [xi;xi+1] аппроксимируется интерполяционным многочленом 1-го порядка, а затем интегрируется методом трапеции?
- Что является начальными условиями ОДУn-го порядка (для n=2)?
29.Сколько ОДУ 1-го порядка будет содержать система, построенная для решения n-го порядка?
|





 ?
? ?
?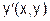 в модифицированном методе Эйлера?
в модифицированном методе Эйлера?