ПОЗНАВАТЕЛЬНОЕ

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Точное аналитическое решение заданного дифференциального уравнения

Вопросы, подлежащие изучению

1.Постановка задачи численного решения обыкновенных дифференциальных уравнений. Задача Коши.

1.Методы Рунге-Кутты различных порядков, общие свойства.

2.Погрешности методов.

3.Выбор шага интегрирования.

4.Графическая иллюстрация методов Рунге-Кутты.

Задание

1. Выбрать индивидуальное заданиевтабл. 6.5-1 для решения обыкновенных дифференциальных уравнений:

· дифференциальное уравнение ;

· интервал [a;b] , где ищется решение дифференциального уравнения;

· начальные условия x₀, y₀;

· шаг интегрирования h₀_.

2. Найти аналитическое решение заданного дифференциального уравнения, полагая его точным.

3. Вычислить значения полученного решения на отрезке [a;b] с шагом h₀.

4. Найти численное решение дифференциального уравнения методом Эйлера - в точках отрезка [a;b] с шагом h₀ с помощью «ручного счета».

5. Вычислить значения погрешностей для , , .

6. Составить схему алгоритма, написать программу интегрирования дифференциальных уравнений методом Рунге-Кутты 4-го порядка с автоматическим выбором шага и провести контрольное тестирование на примере, рассмотренном в п. 6.5.5.

7. Получить решение «расчетом на ПК» с шагом h₀ и E =10^-4.

8. Вычислить значения погрешностей ,

9. Графически проиллюстрировать решения .

Получить решение с помощью математических пакетов.

Варианты задания

Таблица 6.5-1

№ вар	Уравнение	x₀	y₀	h₀	a	b
	y' = x y²		-2	0.4
	y' = y² (x²+ x + 1)		-2	0.2
	y' = x³ y²		-2	0.2
	y' = y / cos²(x)			0.1
	y' = y cos(x)			0.5
	y' = y² cos(x)		-1	0.4
	y' = x² y + y			0.2
	y' = (x – 1)² y²		-1	0.5
	y' = x³ y			0.2
	y' = y² sin(x)		0.5	0.2
	y' = y sin(x)			0.4
	y' = x y			0.2
	y' = y² / x			0.2
	y' = x² y			0.2
	y' = y² (2 – x)		-1	0.4
	y' = 3 x² y²		-4	0.2
	y' = y² (e^x + 4x)		-1	0.4
	y' = y (x – 1)			0.4
	y' = x (1 + y²)			0.2		1.6
	y' = x / (2y)			0.4
	y' = y / (3 x²)			0.2
	y' = 4 x e^-3y			0.2
	y' = 2 x y			0.2
	y' = 2 x (y^1/2)			0.4
	y' = y² e^x		-2	0.4
	y' = x (1 – y²)^1/2			0.4		1.6
	y' = (1 + x) y			0.2
	y' = x² (1 – y²)^1/2			0.4		1.6
	y' = (x² + x) y²		-1	0.4
	y' = y² / cos²(x)		-1	0.3		1.5
	y' = y²sin x			0.1
	y' = cos(x) y			0.1
	y' =			0.1
	y' = (x-1)² y²			0.1
	y' = y² cos(x)		-1	0.1
	y' = 0.5 y²			0.1
	y' = y² x		-2	0.1
	y' =			0.1
	y' = y² e^x		-1	0.1
	y' = e^-y			0.1
	y' = y (x-1)			0.1
	y' = 3 y² x²		-4	0.1
	y' = (x+1) e^y			0.1
	y' = y cos(x			0.1
	y' = 2y			0.1
	y' =			0.1
	y' =			0.1
	y' = y²/x			0.1
	y' = y /x²			0.1
	y' = (1-x²) /cos(y)			0.1
	y' = (1+y) sin(x)			0.1
	y' = y e^-2x			0.1
	y' = x cos²(y)			0.1
	y' = cos(y)/ (1+x)			0.1
	y' = 0.5 (x+2) y²			0.1
	y' = x cos(y)			0.1
	y' = x²sin(y)			0.1
	y' = y²e^-x			0.1
	y' = y²			0.1
	y' = e^-y/x			0.1
	y' = 3 (sin x) y			0.1
	y' = (cos x) /y			0.1
	y' = x			0.1
	y' = (x-1)² y²/2			0.1
	y' = 1.5 y² cos(x)			0.1
	y' = y²/4			0.1
	y' = 2 y² x³		-2	0.1
	y' = 1.7			0.1
	y' = y² e^x/2		-1	0.1
	y' = ye^-y+x			0.1
	y' = y (x-1)/2			0.1
	y' = 3 (x+1) y²		-1	0.1
	y' = 2 e^y x		-1	0.1
	y' = 0.5 y cos(x)			0.1
	y' = y /5			0.1
	y' = x			0.1
	y' = 2 y²/x			0.1
	y' = (4-x²) cos(y)			0.1
	y' = (2+y) sin(x)			0.1
	y' = y tg(x)			0.1
	y' = y e^x			0.1
	y' = 2 y			0.1
	y' = x sin²(y)			0.1
	y' = 3 x² y			0.1
	y’=0.5 e^x-y			0.1
	y' = y			0.1
	y’=sin(x) e^-y			0.1
	y' = (x/ )y²			0.1
	y' = x² y³/4			0.1
	y' =			0.1

Содержание отчета

1.Индивидуальное задание.

2.Решение ОДУ аналитическим методом.

3.Значения полученного решения y(x) на отрезке [a;b] с шагом , записанные в табл. 6.5-2.

4.Значения численного решения ОДУ, вычисленные методом Эйлера - в точках отрезка [a;b] с шагом h₀_, используя «ручной расчет», и записанные в табл. 6.5-2.

5.Значения погрешностей для , , , записанные в табл. 6.5-2.

6.Схема алгоритма, программа решения дифференциального уравнения методом Рунге-Кутты, результаты контрольного тестирования.

7.Значения решения с шагом h₀ и E =10^-4 , полученные по программе, записанные в табл. 6.5-2 с указанием числа разбиений и фактического шага интегрирования для каждой точки.

8.Значения вычисленных погрешностей , , записанные в табл. 6.5-2.

9.Графическая иллюстрация решений .

10.Решения, полученные с помощью математических пакетов.

Все решения в итоге должны быть оформлены в виде табл. результатов 6.5-2.

Таблица 6.5-2

x_i
…	…	…	…	…	…

Пример выполнения задания

1. Задание для численного решения обыкновенных дифференциальных уравнений:

· дифференциальное уравнение ;

· интервал [0;1];

· начальные условия x₀=0, y₀=1;

· шаг интегрирования h₀=0.1_.

Точное аналитическое решение заданного дифференциального уравнения

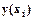
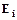
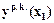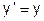Найдем точное аналитическое решение заданного дифференциального уравнения (решение y=y(x))методом разделения переменных. Для этого запишем уравнение в виде и проинтегрируем с учетом начальных условий. Получим . Из начальных условий следует, что с=0.

Аналитическое решение дифференциального уравнения .