 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Коэффициент вариации по среднему квадратичному отклонению - 12
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Государственное образовательное учреждение высшего профессионального образования «Юго-Западный государственный университет» (ЮЗГУ) Кафедра высшей математики
УТВЕРЖДАЮ: Первый проректор − Проректор по учебной работе _____________ Е.А.Кудряшов «____»___________2011г.
НАХОЖДЕНИЕ ЧИСЛОВЫХ ХАРАКТЕРИСТИК СЛУЧАЙНОЙ ВЕЛИЧИНЫ ИЗ ОПЫТА
Методические указания по выполнению лабораторной работы № 28
УДК 510 (083)
Составитель Е.В.Журавлева
Рецензент Кандидат технических наук, доцент кафедры высшей математики Дроздов В.И.
Нахождение числовых характеристик случайной величины из опыта: методические указания к выполнению лабораторной работы №28 / Юго-Зап. гос. ун-т; сост.: Е.В.Журавлева. Курск, 2011. 19 с. табл. 6. Библиогр.: 2. с..
В данной работе содержатся краткие теоретические положения, необходимые для выполнения работы. Работа предназначена для студентов технических специальностей.
Текст печатается в авторской редакции
Подписано в печать _______ . Формат 60х84 1/16. Усл. печ. л. . Уч.-изд. л. .Тираж 50 экз. Заказ. Бесплатно. Юго-Западный государственный университет. 305040 Курск, ул. 50 лет Октября, 94
Содержание
1. Общие положения………………………………………………..4 1.1 Графическое изображение вариационных рядов…………5 1.2 Точечные оценки параметров распределения…………… 1.3 Интервальные оценки параметров распределения……… 2. Использование ЭВМ…………………………………………….. 2.1 Использование программного продукта MATHCAD……. 2.2 Использование программного продукта EXCEL Контрольные вопросы Библиографический список Приложения
Цель работы. 1. Изучить основы методов обработки результатов наблюдения. 2. Ознакомиться с методикой расчета числовых характеристик случайной величины 3. Научиться применять пакет прикладных программ ЕХСЕL при обработке результатов наблюдения
Задание
По исходным данным: 1. Постройте статистический ряд распределения организаций по указанному для каждого варианта признаку. 2. Рассчитайте числовые характеристики дискретного ряда распределения. 3. Постройте интервальный ряд распределения и рассчитайте для него числовые характеристики: выборочное среднее, среднее квадратическое отклонение, коэффициент вариации. 4. Для полученного ряда распределения постройте графики: полигон и кумулятивную кривую. Графически определите значение моды и медианы. 5. Постройте гистограмму и графически определите значение моды. 6. Сравните выборочное среднее для дискретного и интервального рядов между собой. Объясните причину расхождения. Сделайте выводы по результатам выполнения задания.
1. ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
1.1. Вариационные ряды Пусть в результате какого-либо статистического наблюдения конкретного явления получены числовые данные, характеризующие его (для изучения случайной величины X извлечена выборка объема n): x1,x2, . . . ,xn (2.1) Значения x i называют вариантами, m i - число, показывающее, сколько раз встречается вариант x i, называют частотой варианта (mi). Проведя ранжирование вариантов (обычно располагают в порядке возрастания) и указав относительно каждого варианта его частоту, получают статистическое распределение выборки или вариационный ряд. Различают дискретные и интервальные вариационные ряды. Пример 1. При взвешивании 50 одинаковых деталей, изготовленных на одном станке, были получены численные значения веса их в граммах. Вариационный ряд для веса данной детали представлен в табл. 2.1. Таблица 2.1 − Дискретный вариационный ряд
Для построения интервального ряда необходимо определить величину интервала, установить полную шкалу интервалов, в соответствии с ней сгруппировать результаты наблюдений. Для определения оптимальной величины интервала h, при которой ряд не был бы слишком громоздким и, в тоже время, позволил бы выявить характерные черты случайной величины X, используют формулу Стэрджеса
где x min и x max - максимальная и минимальная варианты. За начало первого интервала рекомендуется принимать величину, равную a1 = (x min - h/2), тогда
Построение интервалов продолжают до тех пор, пока начало следующего по порядку интервала не будет равным или большим xmax. Пример 2.Производится замер диаметра (в мм) шейки плунжера после шлифования. Всего исследовалось n = 200 деталей, причем x max = 6.83, x min = 6.68. Величина интервала
a1 = 6.68 - 0.01 = 6.67, a2 = 6.67 + 0.02 = 6.69, . . . a9 = 6.83. Для каждого интервала подсчитывается количество вариант, попавших в данный интервал, причем в интервал включаются варианты больше нижней границы и меньше или равные верхней границы интервала. Таблица 2.2 − Интервальный вариационный ряд
1.2. Графическое изображение вариационных рядов
Графическое изображение вариационных рядов позволяет представить приближенно законы распределения случайной величины X: дифференциальную и интегральную функции распределения. Вариационные ряды могут быть изображены в виде полигона, гистограммы и комулятивной кривой (комуляты).
1.2.1. Полигон и гистограмма
Полигон, как правило, служит для изображения дискретного вариационного ряда. Для построения полигона (полигона относительных частот) на оси абсцисс откладывают значения вариант xi, а на оси ординат относительные частоты wi = mi / n. Точки (xi,wi) соединяют отрезками прямых. Крайние левую и правую точки соединяют соответственно с точками, изображающими варианты, ближайшей снизу к xmin (точка А) и ближайшей сверху к xmax (точка В) (см. рис. 1.1.) Пример 3. Построить полигон для ряда, статистический закон распределения представлен в табл.2.3. Таблица 2.3 − Статистический закон распределения
Полигон представлен на рис.2.1.
Рис.1.1. Полигон дискретного вариационного ряда
Гистограмма служит для изображения только интервального вариационного ряда. Для построения гистограммы (гистограммы относительных частот) на оси абсцисс откладывают частичные интервалы и на них, как на основаниях, строят прямоугольники с высотами, равными wi / h. Здесь wi / h называют плотностью относительной частоты. В результате получается ступенчатая фигура, состоящая из прямоугольников, которая и называется гистограммой. Площадь гистограммы равна единице. Пример 4. Построить гистограмму для ряда из табл.2.2. Значения относительной плотности представлены в табл.2.4.
Таблица 2.4 − Значения относительной плотности частот
Гистограмма для данного ряда представлена на рис.2.2.
Иногда интервальный ряд изображают с помощью полигона. В этом случае интервалы заменяют их серединными значениями и к ним относят интервальные частоты. Для полученного дискретного ряда строят полигон. Полигон изображен на рис.1.2. ломаной линией.
1.2.2. Кумулятивная кривая
Кумулятивная кривая (кривая накопленных относительных частот) строится следующим образом. Если вариационный ряд дискретный, то в прямоугольной системе координат строят точки (xi,wiнак) и соединяют их отрезками; где
причем miнак - накопленная частота, т.е. сумма частот вариант x, удовлетворяющих условию x £ xi. Для вариационного ряда
Пример 5. Построить комуляту для ряда из табл.2.1. Значения накопленных частот представлены в табл.2.5., а комулята на рис.2.3.
Таблица 2.5 − Относительные частоты
Рис.2.3. Кумулятивная кривая
Если вариационный ряд интервальный, то по оси абсцисс откладывают интервалы. Верхним границам интервалов соответствуют накопленные частоты, нежней границе первого интервала - накопленная частота, равная нулю. Значения накопленных частот для интервального ряда из табл.2.2. представлены в табл.2.6., а комулята представлена на рис. 2.4. Таблица 2.6 − Накопленные относительные частоты
Рис.1.4. Кумулятивная кривая для интервального ряда
Таким образом, полигон и гистограмма являются приближением к графику дифференциальной функции распределения случайной величины X, а комулята - интегральной функции распределения для X.
1.2 Точечные оценки параметров распределения
Законы распределения случайной величины полностью ее описывают, однако на практике закон распределения не всегда может быть найден, кроме этого при решении многих практических задач нет необходимости характеризовать случайную величину исчерпывающим образом, а достаточно указать только отдельные числовые характеристики, которые определяют существенные черты распределения случайной величины. Характеристики распределения случайной величины X оценивают посредством характеристик выборки (характеристик вариационных рядов), которые при увеличении n сходятся по вероятности к соответствующим характеристикам X, и при достаточно большом n могут быть приближенно равными им [1 - 5]. К основным несмещенным и состоятельным оценкам [1 - 3] относятся характеристики вариационных рядов: выборочная средняя - `x, исправленная дисперсия - S*2, среднее квадратичное отклонение - S*, коэффициент вариации - V, размах вариации - R, асимметрия - As , эксцесс - Ex , которые определяются по следующим формулам. Средняя арифметическая - `x
или
Дисперсия - S*2
или
Среднее квадратичное отклонение (эмпирический стандарт) - S* S* = или S* =
Коэффициент вариации по среднему квадратичному отклонению -
Размах вариации - R
R = max. Xi - min Xi (2.13)
Асимметрия - As
или
Эксцесс - Ex
или
Средние величины являются обобщающими количественными характеристиками совокупности однотипных явлений по варьирующему признаку. Среднее арифметическое характеризует среднее значение, около которого группируются возможные значения случайной величины, а дисперсия есть мера разбросанности этих значений относительно среднего. Среднее квадратичное отклонение, так же как и дисперсия, является мерой колеблемости, но в отличие от дисперсии представляет собой абсолютную величину, выраженную в тех же единицах, что и варианты. Коэффициент вариации является относительным показателем колеблемости. Вариационный размах (или широта распределения) неустойчивая, чрезвычайно зависящая от случайностей величина, служащая для приблизительной оценки вариации. Асимметрия и эксцесс являются показателями отклонения функции распределения f(x) для X от нормального закона распределения. Если As = 0, то кривая для f(x) симметрична, при As ¹ 0 - асимметрична. Эксцесс характеризует крутизну кривой распределения. Если Ex ¹ 0, то вершина кривой для f(x) находится либо выше (при Ex > 0), либо ниже (при Ex < 0) вершины кривой нормального распределения.
1.3. Интервальные оценки параметров распределения
В п.1.2. были рассмотрены точечные оценки некоторых характеристик распределения случайной величины X через характеристики выборки. Поэтому точечные оценки сами являются случайными величинами, законы которых зависят от закона распределения X и объема выборки n [2]. Чтобы дать представление о точности и надежности точечных оценок используют так называемые доверительные интервалы и доверительные вероятности. Доверительным интервалом для некоторой характеристики Q называют такой интервал (e1,e2), который с заранее выбранной вероятностью Ã содержит истинное значение параметра Q, т.е. P (e1 < Q < e2) = Ã. (2.18) Здесь Ã называют доверительной вероятностью. Обычно значение Ã выбирают близкое к единице: 0,9; 0,95; 0,99; 0,999. a = 1 - Ã называют уровнем значимости.
1.3.1. Построение доверительного интервала для математического ожидания
Если случайная величина X подчиняется нормальному закону распределения, то доверительный интервал для истинного значения x измеряемой величины может быть построен следующим образом. Первый способ. Доверительная оценка при известной точности измерений. Если заранее известно среднее квадратичное отклонение
где n - объем выборки, `x - среднее арифметическое, t(Ã) определяется по заданной доверительной вероятности из условия [1,2]:
2 Ф( t ) = Ã (2.20)
Здесь Ф( t ) = Второй способ. Доверительная оценка при неизвестной точности измерений. Если среднее квадратичное отклонение s заранее неизвестно, то вместо него используют эмпирическое отклонение. Известно [2], что статистика
подчиняется закону Стьюдента с f = n - 1 степенями свободы. Исходя из этого , доверительный интервал в данном случае имеет вид [1,2]
где t (Ã, n - 1) зависит и от объема выборки. t (Ã, n - 1) определяется из таблицы приложения 2.
1.3.2. Построение доверительного интервала для дисперсии и среднего квадратичного отклонения
Известно [2], что статистика
подчиняется закону распределения Пирсона или « c - распределению » с f = n - 1 степенями свободы. Исходя из этого, доверительный интервал для дисперсии s2 случайной величины имеет вид [1,2]
где c12 и c22 - значения, определяемые из таблиц для распределения Пирсона ([3], приложение 5) соответственно для вероятностей Ã1 = (1 - Ã) / 2 и Ã2 = = (1 + Ã) / 2 и числа степеней свободы f = n − 1. Пусть
g12 × S*2 < s2 < g22 × S*2 , (2.25)
где значения g2 протабулированы для n и Ã (приложение 4). Для интервальной оценки среднего квадратичного отклонения служит неравенство
g1 × S* < s < g2 × S* . (2.26)
2. ИСПОЛЬЗОВАНИЕ ЭВМ
2.1. Использование программного продукта MATHCAD
Можно рекомендовать следующий алгоритм выполнения работы с использованием программного продукта MATHCAD. 1.Выписать из таблицы данные для одного статистического ряда. 2.Загрузить MATHCAD. Набрать m:=30(m – объем выборки или количество вариант в данном статистическом ряду), А:=. На математической палитре выбрать «Векторы и матрицы». Сформировать свой вектор, задав число строк матрицы, равное 1, а число столбцов, равное объему выборки. При вводе чисел в матрицу используйте клавишу “Tab” или мышь. 3.Для удобства преобразуем вектор-строку А в вектор-столбец Х. Для этого наберем ниже x:=AT с помощью палитры «Векторы и матрицы», выбрав там операцию транспонирования. 4.Для того чтобы построить дискретный вариационный ряд отсортируем данные в порядке возрастания: x1:=sort(x). Чтобы вывести результат напишем x1T=, нажмем клавишу «Enter» или щелкнем левой кнопкой мыши в произвольном месте, рядом со знаком равно получим результат. По получившейся таблице составим вариационный ряд , подсчитывая вручную частоты вариант. Наберем М1:=. Используя палитру «Векторы и матрицы» сформируем матрицу, состоящую из двух строк и стольких столбцов , сколько встречается различных вариант. В первую строку вводим значения вариант, а во вторую – значения соответствующих частот. Это и будет дискретный вариационный ряд. 5.Для того, чтобы построить полигон, на математической палитре выбираем палитру «Графики», а на ней «Декартов график». Заполняя рабочую область с помощью палитры «Векторы и матрицы», по оси абсцисс вводим (М1Т)<0>, а по оси ординат – (М1Т)<1>. Щелкнув мышью вне области графика, получим полигон частот. 6.Для построения интервального вариационного ряда воспользуемся формулой Стэрджеса, чтобы найти оптимальный шаг. Введем
Выведем полученные значения x1i= ; x2т= . Подчитаем число вариант, попавших в каждый интервал: L:=hist(x2,x1т). Таким образом, интервальный вариационный ряд имеет вид x1т, Lт. 7. Для того чтобы построить гистограмму найдем относительные плотности частот, которые получим следующим образом:
8. Для построения кумулятивной кривой необходимо сначала получить матрицу накопленных частот. Для этого введем следующее: g:=(M1т)<1>, i:= 0..0,i1 yi= где yi – значения накопленных частот, il – количество столбцов в матрице М1. При построении кривой воспользуемся палитрой «Декартов график». Заполняя рабочую область, по оси X введем X введем (М1т) )<0>, а по оси Y – g. Щелкнув мышью вне области графика, получим изображение искомой кривой. 9. Для нахождения числовых характеристик: среднего выборочного, средней выборочной дисперсии, выборочного среднего квадратичного отклонения, размаха выборки и др. необходимо ввести соответствующие формулы с помощью математической палитры и встроенных в нее палитр и рядом вывести получившиеся значения. Например,
среднее выборочное
выборочная дисперсия S*2:=
выборочное среднее квадратичное отклонение
S*: 10. Для того чтобы доверительный интервал для математического ожидания при неизвестной точности измерений необходимо воспользоваться следующей формулой:
где
Р – доверительная вероятность; n – объем выборки; S* - исправленное среднее квадратичное отклонение. Взяв значения выборочных характеристик из п.8, а квантиль распределения из таблиц, найдем значения концов интервала ε1, ε2. Пусть Р:=0,95, m:=30, t:=2,05 ε1:= xcp-
ε2:= xcp- 11. Для того чтобы построить доверительный интервал для дисперсии, необходимо по таблицам найти квантали распределения Пирсона и воспользоваться следующими формулами:
Здесь
где х2(Р,n) – квантиль распределения Парсона; S*2 – исправленная выборочная дисперсия; n – объем выборки;
Зададимся доверительной вероятностью Р:=0,99, по таблицам найдем
Тогда δ1:= Искомый интервал и будет (δ1, δ2).
12 |



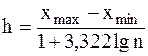 , (2.2)
, (2.2) , где i = 2,3,... (2.3)
, где i = 2,3,... (2.3)
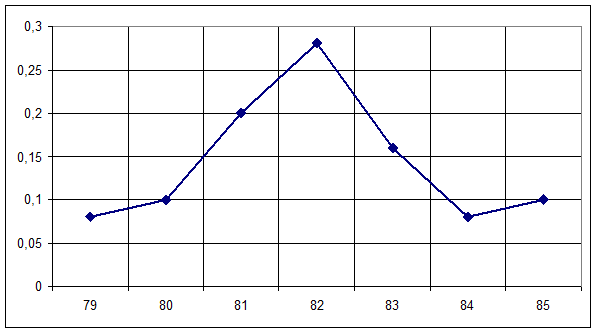
 Рис.1.2. Гистограмма
Рис.1.2. Гистограмма

 , (2.4)
, (2.4) , (2.5)
, (2.5)

 (2.6)
(2.6)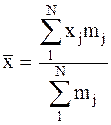 (2.7)
(2.7) (2.8)
(2.8) (2.9)
(2.9) =
=  (2.10)
(2.10) (2.11)
(2.11) (2.12)
(2.12) (2.14)
(2.14) (2.15)
(2.15) (2.16)
(2.16) (2.17)
(2.17) (или другая связанная с ней характеристика точности измерений), то доверительный интервал имеет вид
(или другая связанная с ней характеристика точности измерений), то доверительный интервал имеет вид , (2.19)
, (2.19) - функция Лапласа, значения которой представлены в таблице приложения 1.
- функция Лапласа, значения которой представлены в таблице приложения 1. (2.21)
(2.21) , (2.22)
, (2.22) (2.23)
(2.23)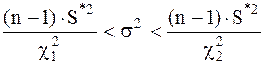 , (2.24)
, (2.24) , тогда (2.24) примет вид
, тогда (2.24) примет вид . Выведем значение h. Округлим полученное значение до одного знака после запятой и введем его в качестве h. Посчитаем число интервалов:
. Выведем значение h. Округлим полученное значение до одного знака после запятой и введем его в качестве h. Посчитаем число интервалов: и выведем его. Сформируем границы интервалов: j:=1..ml+1; x1i:=min(xl); x2j:=x1i+h*(j-1,5).
и выведем его. Сформируем границы интервалов: j:=1..ml+1; x1i:=min(xl); x2j:=x1i+h*(j-1,5). . Затем на палитре «Графики» выбрать трехмерную гистограмму. В рабочей области гистограммы ввести массив L, щелкнув мышью вне графика, получим изображение гистограммы. В отчете необходимо будет проставить концы интервалов по оси Х самостоятельно.
. Затем на палитре «Графики» выбрать трехмерную гистограмму. В рабочей области гистограммы ввести массив L, щелкнув мышью вне графика, получим изображение гистограммы. В отчете необходимо будет проставить концы интервалов по оси Х самостоятельно.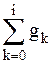 yт= . ,
yт= . , xcp= ;
xcp= ; S*2= ;
S*2= ; S*=
S*=
 <М[x]<
<М[x]<  ,
, - выборочная средняя;
- выборочная средняя; - квантиль распределения Стьюдента;
- квантиль распределения Стьюдента; ε1= ;
ε1= ;
 S*2<D[x]<
S*2<D[x]<  S*2 или
S*2 или  S*2<D[x]<
S*2<D[x]<  S*2
S*2 =
=  ,
,  =
= 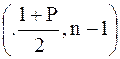 ,
,