 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Порядок выполнения работы. 12
Лабораторная работа № 6 Гармонические колебания. Теоретическое введение.Пружинным маятником называют колебательную систему, представляющую собой материальную точку массой Период колебаний пружинного маятника Математический маятник — это колебательная система, состоящая из материальной точки массой Если точка подвеса математического маятника покоится или движется равномерно прямолинейно относительно инерциальной системы отсчета, связанной с поверхностью Земли, то период малых колебаний математического маятника Формула для определения периода согласуется с экспериментальными законами малых колебаний математического маятника, которые были открыты Галилеем. Согласно этим законам, период малых колебаний математического маятника не зависит от амплитуды колебаний и массы маятника. Кроме того, этот период прямо пропорционален корню квадратному из длины маятника и обратно пропорционален корню квадратному из ускорения свободного падения. Если точка подвеса математического маятника движется в гравитационном поле Земли с ускорением
Цель опытов. Обеспечить овладение экспериментальными методами проверки законов колебаний пружинного и математического маятников и выяснение границ их применимости.
Работа 6.1.1. Изучение колебаний пружинного маятника. Цель работы:Исследованиезависимости характеристик пружинных маятников от амплитуды колебаний, массы грузов и жесткости пружины. Оборудование: штатив с двумя зажимами, пружина с держателем, два груза различной массы, весы, разновес, секундомер, оптический датчик. Порядок выполнения работы. 1. Установка для выполнения опыта схематически изображена на рисунке 1.
Рис. 1
2. Для экспериментального исследования законов колебаний пружинного маятника закрепите в лапках штатива держатель пружины и оптоэлектрический датчик. 3. Подключите оптоэлектрический датчик к гнезду 1на задней панели цифрового секундомера. Включите прибор и переключите секундомер в режим (г P ) измерения периода колебаний. 4. Закрепите в держателе штатива пружинный маятник в вертикальном положении. 5. Убедитесь, что груз маятника свободно проходит через створ оптического датчика. 6. Выведите маятник из положения устойчивого равновесия и не менее трех раз измерьте период колебаний при различных значениях амплитуды колебаний. Результаты измерений занесите в таблицу 1. Убедитесь, что период Т колебаний не зависит от амплитуды А колебаний. 7. Повторите измерения периода колебаний маятника при других значениях массы груза, проверьте выполнимость соотношения 8. Измените, жесткость пружины, зафиксировав металлическими скобами сначала четверть, а затем половину ее длины. 9. Измерьте абсолютные удлинения 10. Повторите измерения периода колебаний маятника при различных значениях жесткости, проверьте выполнимость соотношения 11. Рассчитайте отношение экспериментально измеренного значения периода колебаний маятника к рассчитанному теоретически значению 12. Результаты измерений и вычислений занесите в таблицу. Таблица 1
12 |



 , закрепленную на одном конце спиральной пружины, другой конец которой неподвижен (пружина может находиться как в вертикальном, так и в горизонтальном положении). Причем в простейшем случае закрепленный конец пружины находится в покое относительно инерциальной системы отсчета, в которой происходят колебания маятника. Внутренними силами, которые вызывают колебательное движение пружинного маятника, являются силы упругости пружины.
, закрепленную на одном конце спиральной пружины, другой конец которой неподвижен (пружина может находиться как в вертикальном, так и в горизонтальном положении). Причем в простейшем случае закрепленный конец пружины находится в покое относительно инерциальной системы отсчета, в которой происходят колебания маятника. Внутренними силами, которые вызывают колебательное движение пружинного маятника, являются силы упругости пружины. , где
, где 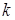 — жесткость пружины. При точных расчетах периода и частоты колебаний пружинного маятника необходимо учитывать также массу пружины
— жесткость пружины. При точных расчетах периода и частоты колебаний пружинного маятника необходимо учитывать также массу пружины 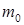 . В этом случае
. В этом случае  , где
, где  .
. и способная совершать колебания в гравитационном поле Земли, или в другом силовом поле. В реальных условиях — это тело, масса которого во много раз больше массы нити, а размеры малы по сравнению с длиной нити (колебательная система состоит из материальной точки, нити и гравитационного поля Земли). Внутренней силой, вызывающей колебательное движение, является равнодействующая силы тяжести и силы упругости нити.
и способная совершать колебания в гравитационном поле Земли, или в другом силовом поле. В реальных условиях — это тело, масса которого во много раз больше массы нити, а размеры малы по сравнению с длиной нити (колебательная система состоит из материальной точки, нити и гравитационного поля Земли). Внутренней силой, вызывающей колебательное движение, является равнодействующая силы тяжести и силы упругости нити. , где
, где  — длина маятника, ускорение силы тяжести.
— длина маятника, ускорение силы тяжести.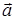 , которое направлено под углом
, которое направлено под углом  к ускорению силы тяжести
к ускорению силы тяжести  , то период малых колебаний маятника определяется по формуле
, то период малых колебаний маятника определяется по формуле  , где
, где  .
.
 и покажите, что период колебаний Т прямо пропорционален корню квадратному из массы груза.
и покажите, что период колебаний Т прямо пропорционален корню квадратному из массы груза.
 пружины с незафиксированными и с зафиксированными витками, подвесив к ней груз, масса
пружины с незафиксированными и с зафиксированными витками, подвесив к ней груз, масса  .
. и покажите, что период колебаний Т обратно пропорционален корню квадратному из жесткости пружины
и покажите, что период колебаний Т обратно пропорционален корню квадратному из жесткости пружины  .
. и проверьте справедливость формулы
и проверьте справедливость формулы  , м
, м
 , м
, м
 , с
, с