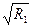 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Определение радиуса кривизны линзы с помощью колец Ньютона
(«Оптика», «Кольца Ньютона») Цель работы: •Знакомство с моделированием явления интерференции света в тонких плёнках. • Изучение интерференции полос равной толщины в схеме колец Ньютона. • Определение радиуса кривизны линзы.
Краткая теория: Классическим примером полос равной толщины являются кольца Ньютона. Они наблюдаются при отражении света от воздушного зазора, образованного плоскопараллельной пластинкой и соприкасающейся с ней плосковыпуклой линзой с большим радиусом кривизны (рис.1).
Если на линзу падает пучок монохроматического света, то световые волны, отражённые от верхней и нижней поверхностей воздушной прослойки, будут интерферировать между собой. При этом образуются интерференционные полосы, имеющие форму концентрических светлых и тёмных колец убывающей ширины. В отражённом свете оптическая разность хода с учётом потери полуволны будет равна
где d- толщина воздушного зазора. Из рис. 1 следует, что
Учитывая, что ct является величиной второго порядка малости, то из (2) получим
Следовательно,
В точках, для которых оптическая разность хода равна
возникают тёмные кольца. Из формул (4) и (5) радиус k-ого тёмного кольца будет равен
Формула (6) позволяет определить радиус кривизны линзы
Вследствие деформации стекла, а также наличия на стекле пылинок невозможно добиться плотного примыкания линзы и пластины в одной точке. Поэтому при определении радиуса кривизны линзы пользуются другой формулой, в которую входит комбинация из двух значений радиусов интерференционных колец rm и rn, что позволяет исключить возможный зазор в точке контакта линзы и стеклянной пластины:
Методика и порядок измерений: 1. Зацепив мышью движок регулятора длины волны монохроматического света и установите первое значение длины волны из таблицы 1 для вашей бригады. Аналогичным образом установите первое значение радиуса кривизны линзы R
Таблица 1.Значение длины волны и радиуса кривизны линзы.
2. По формуле
Таблица 2. Результаты измерений и расчетов.
3. По формуле (7) для m1=3 и n1=5, m2=4 и n2=6 рассчитайте радиусы кривизны линзы R1 и R1* и запишите значения в таблицу 2.
4. Установите мышью второе значения радиуса кривизны линзы и длины волны из таблицы 1 и выполните измерения п.п. 3 и 4.
5. Проанализируйте полученные результаты и оцените погрешность проведённых измерений.
Ответ: По результатам измерений и расчётов получены значения радиусов кривизны линз, равные R1=( ± ) R2=( ± )
Вывод по ответу Полученные экспериментально значения радиусов кривизны линз равные и с точностью до ошибок измерений, составляющих и совпадает (не совпадает) с установленными значениями данных величин и .
Вопросы и задании для самоконтроля 1. Что называется интерференцией? Каковы условия наблюдения интерференции? 2. Какие волны называются когерентными? Назовите способы получения когерентных волн? 3. Проведите расчёт интерференционной картины в тонкой плёнке. 4. Запишите условия минимума и максимума интерференции. 5. Выведите формулу для вычисления темных и светлых колец Ньютона. 6. Как изменится картина колеи Ньютона, если воздушный зазор между линзой и пластиной заполнить водой? 7. Почему в отражённом свете в центре наблюдаемся темное кольцо? 8. Как изменится картина колец Ньютона, если наблюдение проводить в проходящем свете? 9. Почему масляное пятно на поверхности жидкости имеет радужную окраску? 10. Объясните, как явление интерференции света в тонких плёнках используется для просветления оптики? Запишите формулу для определения толщины просветляющей пленки.
ЛАБОРАТОРНАЯ РАБОТА №4. ДИФРАКЦИОННАЯ РЕШЕТКА («Оптика», «Дифракционная решётка») Цель работы: •Знакомство с моделированием процесса сложения когерентных электромагнитных волн. •Экспериментальное исследование закономерностей взаимодействия световых волн с периодической структурой (дифракционной решеткой). Краткая теория: ДИФРАКЦИОННОЙ РЕШЕТКОЙ называется совокупность большого числа N одинаковых, отстоящих друг от друга на одно и то же расстояние, прямоугольных щелей в плоском непрозрачном экране. ПЕРИОДОМ (постоянной) дифракционной решетки называется расстояние d между серединами соседних щелей или сумма ширины щели b и ширины непрозрачного участка а. При анализе излучения, проходящего через решетку, обычно используют линзу и экран, расположенный в фокальной плоскости линзы на расстоянии L от нее. Линза собирает параллельные лучи в одну точку на экране. Положение X точки на экране зависит от угла падения θ лучей на линзу: X=Lsin(0). Для очень малых углов sin(θ) и Х = θL РАЗНОСТЬ ХОДАлучей от соседних щелей Δ = dsin(θ). РАЗНОСТЬ ФАЗ лучей от соседних щелей ИНТЕНСИВНОСТЬ ИЗЛУЧЕНИЯ, идущего от решетки под углом θ:
где I0 - интенсивность, создаваемая одной щелью против центра линзы, b-ширина щели. Первый множитель обращается в 0 в точках, для которых bsin(θk) = ±кλ (к ~ 1,2,...). Второй множитель принимает значение N2 в точках, удовлетворяющих условию dsin(θm) = ±mλ (т=- О,1,2,.,.). Последнее условие определяет положение ГЛАВНЫХ МАКСИМУМОВ излучения, a m называется порядком максимума. Интенсивность в главном максимуме преобразуем, раскладывая синус в ряд и ограничиваясь первыми двумя членами разложения:
Обозначим Отношение Rm интенсивности в m-том максимуме к интенсивности в нулевом максимуме называется «относительной интенсивностью m-того максимума».
Формулу соответствующего графика получить ширину щели.
МЕТОДИКА и ПОРЯДОК ИЗМЕРЕНИЙ:
1. При включении программы моделирования автоматически устанавливаются следующие параметры: порядок максимума m=l, длина волны 0.45 мкм, расстояние между щелями d = 20 мкм. Нажимая левую кнопку мыши, установив ее маркер на дифракционной картине, меняйте т от 0 до 3 и наблюдайте изменение числового значения координаты максимума на экране. Установите длину волны излучения, соответствующую желтому цвету и, меняя т и d, снова наблюдайте картину интерференции. 2. Установите расстояние между щелями d= 20 мкм. 3. Подведите маркер мыши к кнопке на спектре и нажмите левую кнопку мыши. Удерживая кнопку в нажатом состоянии, перемещайте кнопку до тех пор, пока над спектром не появится значение длины волны, равное величине из таблицы 1 для вашей бригады. 4. Измерьте линейкой на экране монитора длины светящихся отрезков, соответствующих интенсивности соответствующих максимумов на дифракционной картине. Запишите значения интенсивности в таблицу 2, 5. Увеличивая d на 1 мкм, повторите измерения по п.З. 6. Установив новое значение длины волны из таблицы 1, повторите измерения, записывая результаты в таблицу 3.
Таблица 1. Примерные значения длины волны
Таблицы 2 Результаты измерений при λ1= нм.
Таблицы 3 Результаты измерений при λ2= нм.
ОБРАБОТКА РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЕТА: 1,Вычислите и запишите в таблицы 2 и 3 корни из относительных амплитуд максимумов. Постройте по таблице 2 на одном рисунке графики экспериментальных зависимостей корня из относительной амплитуды от обратного квадрата периода решетки для всех максимумов (указав на них номер максимума). На втором рисунке постройте результаты по таблице 3.
2. По наклону каждого графика определите экспериментальное значение ширины щели, используя формулу
3. Вычислите среднее значение ширины щели, проанализируйте ответы и графики. Истинное значение b=5 мкм.
Вопросыи задания для самоконтроля 1. Дайте определение световой волны. 2. Дайте определение гармонической волны. 3. Дайте определение электромагнитной волны. 5. Какие волны называются когерентными? 6. Дайте определение дифракции. 7. Что такое дифракционная решетка? 8.Для каких целей используется дифракционная решетка? 9. Что такое постоянная (период) дифракционной решетки? 10.Зачем между дифракционной решеткой и экраном ставится собирающая линза? 11.Напишите формулу разности хода лучей, идущих от двух соседних щелей дифракционной решетки. 12.Напишите формулу разности фаз лучей от соседних щелей. 13.Как формируются главные максимумы дифракционной картины? ЛАБОРАТОРНАЯ РАБОТА №5. |
(1)
(2)
(3)
(4)
(5)
(6)
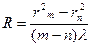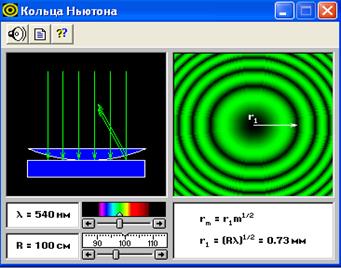
(7)
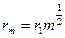и указанному значению r1 в правом нижнем прямоугольнике окна опыта рассчитайте значение радиусов3,4,5, и 6-го тёмных колец Ньютона и запишите эти значения в таблицу 2.
можно проверить экспериментально и из
