 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Примеры расчета действительных погрешностей базирования 12
Поверхности, по которым базируются заготовки, обычно имеют плоскую, цилиндрическую или, реже, коническую форму, В отдельных случаях заготовки базируются сразу по нескольким таким поверхностям, однако, число наиболее употребительных комбинаций невелико. Также ограничено число принципиально различных устройств, предназначенных для базирования. Установка по плоскости. На рис. 3.3 представлен наиболее простой случай: заготовка базируется по плоской поверхности; требуется выдержать размер 30-0,15 (рис. 3.3,а).
а) б) Рис. 3.3 Варианты простановки размеров на операционном чертеже. Примем среднюю экономическую точность D=0,1 мм (предварительное фрезерование по 10-му квалитету). Следовательно, [eб.]=0,15 - 0,1 = 0,05 мм. Выдерживаемый размер 30-0,15 связывает обрабатываемую поверхность с нижней поверхностью М, являющейся, следовательно, исходной базой. Поскольку поверхность М опирается на неподвижную поверхность (стола станка или приспособления), которая в процессе обработки не поднимается и не опускается, геометрически исходная база у всех заготовок будет находиться в неизменном по высоте положении, т.е. eб.действ.= 0. Поэтому выдержать заданный допуск вполне возможно. Теперь допустим, что при тех же условиях обработки нужно выдержать с тем же допуском размер 20+0,15 (рис.3.3,б). Здесь дело обстоит иначе. Поскольку выдерживаемый размер 20+0,15 связывает обрабатываемую поверхность не с нижней поверхностью М, а с верхней N, последняя является исходной базой. При намеченной схеме базирования положение исходной базы обуславливается размером 50-0,2 . Поэтому полный дифференциал по формуле (3) D 20 = D50 и eб.действ. = Т50 = 0,2 мм, а, т.к. допуск по выдерживаемому размеру не изменился и [eб.] = 0,05 мм то, очевидно, что действительное значение поля рассеивания погрешностей базирования больше допустимого. Если принять намеченную схему базирования, получится брак.
Чтобы сделать eб.действ. £ [eб.], можно осуществить одно из следующих мероприятий: 1. Увеличить допуск по размеру 20; 2. Сузить допуск по размеру 50; 3. Изменить схему базирования. Если исходную базу(поверхность N) будем прижимать к неподвижному упору, то получим eб.действ. = 0 (рис. 3.4).
Рис. 3.4. Схема усовершенствованного фрезерного приспособления: 1 - клин; 2 - неподвижный упор (элементы приспособления).
Установка вала в призме. В качестве исходного примера рассмотрим случай установки деталей в призме по наружной цилиндрической поверхности, приведенный на рис.3.5, где в детали требуется профрезеровать паз. В соответствии с конструкторскими соображениями может потребоваться соблюдение любого из размеров h, m или n ( см. рис.3.2). В зависимости от того, какой из этих размеров ограничен на чертеже соответствующим допуском, возможны принципиально различные случаи. В первом случае исходной базой служит центр С, во втором - точка А, в третьем - точка В ( см. рис.3.2). Схема базирования цилиндров и дисков с помощью призмы является основной: расчетные погрешности базирования других способов установки цилиндров и дисков получаются как частные случаи.
Рис. 3.5. Исходные данные для расчета действительной погрешности базирования при установке заготовки в призме: 1 - заготовка; 2 - призма.
1. Требуется выдержать размер h. Положение исходной базы - центра С по отношению к призме (технологическая база - точка О) обуславливается вектором ОС. Проецируя этот вектор на направление выдерживаемого размера h, получим:
L = MC = OC cos g.
Из DOCK находим где a - угол призмы, D - диаметр заготовки. Следовательно,
Полный дифференциал:
а поле рассеивания погрешности базирования eб.действ где TD - допуск по диаметру заготовки. Как видно из выражения (8) , eб.действ при данном угле призмы a зависит от угла g. В случае, если g = 0 eб.действ при g=45° и a=90° eб.действ Схему базирования, показанную на рис.3.6 , можно рассматривать как случай, когда g=90°, поэтому eб.действ = 0.
Рис. 3.6. Случай g=90° при базировании в призме.
При установке в самоцентрирующем приспособлении (в трехкулачковом самоцентрирующем патроне, самоцентрирующих тисках и т.д. ) центр всех заготовок, независимо от их диаметра, будет занимать неименное положение. Вследствие этого, как и в предыдущем случае eб.действ = 0.
2. Требуется выдержать размер m (рис. 3.7) .
Рис. 3.7. Расчетная схема базирования в призме при выдерживании размера m. Положение исходной базы - точки А - по отношению к призме обуславливается вектором ОА. Проецируя этот вектор на направление размера m, получим :
L = MA = CM - CA.
Из D ОСМ имеем : СМ = OC cos g = Очевидно, что CA = Следовательно, L = Тогда полный дифференциал по формуле (3) : DL = а поле рассеяния, соответствующее действительной погрешности базирования, составит eб.действ
Погрешность базирования равна нулю в следующих случаях: а) если cosg = sin (a/2), в частности, при a = 90°, если g = 45° ; б) при g = 0° и a = 180° (т.е. при установке на плоскость). При базировании по схеме, показанной на рис.6, что соответствует g = 90°, eдейств
В случае, когда g = 0 eб.действ 3. Требуется выдержать размер n( рис. 3.8). Положение исходной базы - точки В относительно призмы обуславливается вектором ОВ. Проецируя последний на направление выдерживаемого размера n, получим: L = MB = MC + CB =
Рис. 3.8. Расчетная схема базирования в призме при выдерживании размера n. Тогда полный дифференциал по формуле (3): DL = а поле рассеяния, соответствующее действительной погрешности базирования, составит: eб.действ ри g = 0° , имеем : eб.действ
При g = 90° и a = 180° оказывается, что eб.действ = ТD.
Сопоставление различных схем базирования
Допустим, что у диска, показанного на рис. 3.9,а, нужно просверлить отверстие и выдержать размер m с соответствующим допуском. Сравним при помощи выведенных зависимостей две схемы кондукторов, схематически показанных на рис. 3.9,б) и в).
а) б) в)
Рис. 3.9. Варианты конструкции сверлильного приспособления - кондуктора.
Схема кондуктора на рис. 3.9,б аналогична схеме, приведенной для размера m выше (см. рис. 3.2) при g = 0° (см. рис. 3.5). Поэтому e’б.действ Схема кондуктора на рис. 3.9, в) аналогична схеме, приведенной выше для размера n (см. рис. 3.2), следовательно, e’’б.действ Отношение
При a=90° Таким образом, несущественная, с первого взгляда, разница в схемах конструкций кондукторов ведет к увеличению значения eб.действ при второй схеме по сравнению с первой почти в 6 раз.
12 |







 .
. ,
, , (8)
, (8)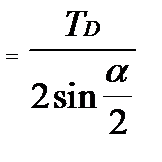 ;
; .
.

 .
.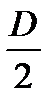 .
. .
.
 ,
, .
. .
. .
.
 ,
, .
.

 (11)
(11)