ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Расчетные формулы для определения параметров регрессии и корреляции 12
Система нормальных линейных алгебраических уравнений относительно
Решение системы: a = 2.38315; b = 0,00868. Коэффициент регрессии (альтернативные формулы)
Свободный член уравнения регрессии
Коэффициент корреляции
Индекс корреляции
Коэффициент детерминации
Скорректированный коэффициент детерминации
Более 76% дисперсии результативного показателя (Стоимость полиграфических работ) обусловлено изменением фактора-аргумента (Объем заказа в тыс. л.-отт.). По этому показателю рассматриваемая модель регрессии удовлетворяет необходимым требованиям.
Стандартная ошибка регрессии
F-критерий Фишера
Fтабл =FРАСПОБР(0.05;1;25) = 4.2417
Fтабл =FРАСПОБР(0.01;1;11) = 7.7698
При уровне значимости a = 0,05 и при более строгом подходе (a = 0,01) уравнение регрессии в целом является значимым.
Стандартные ошибки параметров регрессии и коэффициента корреляции
Расчетные значения T-критериев Стьюдента
Соотношение между T-критериями Стьюдента и F-критерием Фишера
Табличное значение T-критерия Стьюдента Tтабл =СТЬЮДРАСПОБР(0.05;25) = 2.05954
Tтабл =СТЬЮДРАСПОБР(0.01;25) = 2.7874
При уровне значимости a = 0,05 и при a = 0,01 параметры уравнения регрессии a и b, а также коэффициент корреляции r являются значимыми.
Точечный прогноз
Ошибка прогноза
Доверительный интервал прогноза с учетом индивидуального рассеивания результирующего показателя при x = 1.1xсредн.
Доверительный интервал прогноза без учета индивидуального рассеивания результирующего показателя при x = 1.1xсредн.
Доверительные интервалы прогноза с учетом и без учета индивидуального рассеивания результирующего показателя при различных значениях x
Результаты расчетов с помощью пакета
Матричные вычисления
Расчеты с помощью пакета STATISTICA
Линейная модель
Параметры регрессии
Регрессионные остатки
Доверительные интервалы прогноза
Пунктирная линия на графике соответствует прогнозу для значения фактора, превышающего на 10% его среднюю величину (ранее было получено: 1,49376 ≤ yр ≤ 9,37264).
Парная нелинейная регрессия
Гипербола
Результаты расчетов совпадают с полученными ранее в Excel:
Дополнительно получена скорректированная величина индекса детерминации 0,2286 и уровни значимости свободного члена и коэффициента регрессии.
Обратная функция
Результаты расчетов в Excel:
Для гиперболической и обратной функций регрессии результаты, полученные пакетом STATISTICA, полностью совпадают с параметрами линеаризованных моделей регрессии, рассчитанных ранее с помощью функции Excel "ЛИНЕЙН".
12 |








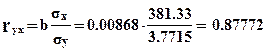




 (для парной линейной регрессии).
(для парной линейной регрессии).