 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| УРАВНОВЕШИВАНИЕ ВРАЩАЮЩИХСЯ МАСС, РАСПОЛОЖЕННЫХ В ПАРАЛЛЕЛЬНЫХ ПЛОСКОСТЯХ
В общем случае неуравновешенные массы расположены на разных дисках, хотя те и насажены на один вал. Получается, что массы вращаются в параллельных плоскостях, каждая из которых перпендикулярна оси вращения звена. Поэтому именно здесь решаются задачи статистического и динамического уравновешивания (п. 4.1). Даны неуравновешенные массы m1, m2, m3, которые устанавливаются на неуравновешенные (средних) дисках; r1, r2, r2 - радиус-векторы их центров тяжести: α1, α2, α2,- углы расположения неуравновешенных масс, которые отмеряются по часовой стрелке от вертикальной оси. При статическом уравновешивании ротор находится в состоянии покоя под действием сил тяжести. Поэтому уравнение равновесия одно и будет удовлетворять условию: SFиi= 0, Fи1 + Fи2 + Fи3 + Fур= 0. (4.1) Необходимо определить массу одного противовеса. В данном случае противовес будет устанавливаться на крайних дисках, которые называются плоскостями уравновешивания I и II (рис. 2, а). Центробежная сила инерции вычисляется по формуле: Fи = mw2r. (4.2) Масса груза определится из формулы силы тяжести: m = G/g. Тогда уравнение равновесия (4.1) примет вид:
где w - угловая скорость вращения вала с диском, на котором расположены грузы. Преобразуем выражение (4.3), получим формулу (1):
Т.к. отношение
Каждый вектор
Высчитываются чертежные значения векторов
и строится план сил (рис. 2, б). Замыкающий вектор укажет направление того радиуса, на котором расположен противовес. Определяем его действительное значение Gурrур = Массу противовеса вычисляем методом подбора. Для этого считаем радиус установки противовеса:
Массу противовеса подбираем из набора масс так, чтобы численное значение радиуса попало в пределы радиусов установки грузов (см. п.1. «Технические данные ротора»). Противовес вычисленного груза устанавливается на любой плоскости уравновешивания (I или II). В данном примере противовес установлен на первой плоскости (рис. 2, а). Для определения уравновешивающего угла αур необходимо вектор При динамическом уравновешивании ротор приводится во вращение с угловой скоростью w. Поэтому, чтобы уравновесить систему, нужно решить два уравнения равновесия SFиi = 0, SMиi = 0. Следовательно, наименьшее число противовесов будет 2.
SFиi= 0, Fи1+ Fи2+ Fи3+ FI + FII = 0. (4.7) SMиi = 0; Fи1a1 + Fи2а2 + Fи3 а3 + FиIIa = 0. Известно, что центробежная сила инерции вычисляется по формуле (4.2). Тогда уравнения (4.7) примут вид:
где а1, а2, а3 - расстояния между плоскостью уравновешивания дисками; а – расстояние между I и II плоскостями уравновешивания. Так же как и в предыдущем случае (для статического уравновешивания), система уравнений решается графически построением векторных уравнений. Сначала решается 2-ое уравнение. Считается масштабный коэффициент mGrа:
Затем рассчитываются чертежные значения векторов
Рис. 2. Статистическое и динамическое уравновешивание ротора: а - кинематическая схема ротора; б - план сил для статического уравновешивания; в, г - планы сил для динамического уравновешивания
Строится план сил (рис. 2, в) и определяется действительное значение полученного вектора: GIIrIIа = Методом подбора находятся уравновешенная на плоскость II масса mII и радиус-вектор ее центра тяжести rII
Массу противовеса подбираем из набора масс так, чтобы численное значение радиуса попало в пределы радиусов установки грузов (см. п. 1. «Технические данные ротора»). Затем приступают к решению 1-го уравнения. Для этого у найденного произведения исключают расстояние а GIIrII = GIIrIIа / a = (Hм). Высчитывают масштабный коэффициент mGr = G1r1 / [G1r1] = (Hм/мм) и строят план сил. Вектор GIIrII переносят параллельно вектору GIIrIIа с предыдущего плана (рис. 2, г). Замыкающий вектор покажет направление радиус-вектора Методом подбора определяются mI и rI:
Массу противовеса подбираем из набора масс так, чтобы численные значения радиуса находились в пределах радиусов установки грузов (см. п. 1. «Технические данные ротора»). Найденные массы устанавливаются: mII - на плоскость II, mI – на плоскость I. Для определения углов αI, αII необходимо вектора Рассмотренный метод уравновешивания может быть применен для определения величины противовесов коленчатых валов многоцилиндровых двигателей.
ПРИМЕРНЫЕ ВОПРОСЫ К ЗАЩИТЕ ЛАБОРАТОРНОЙ РАБОТЫ № 5 1. Задачи уравновешивания механизмов. 2. Рассказать влияние сил инерции на работу механизма и машины в целом. 3. Как достигается балансировка вращающихся масс? 4. Что такое статическое уравновешивание ротора? 5. Что такое динамическое уравновешивание ротора? 6. Рассказать построение схемы механизма (ротора) в масштабе µℓ в двух проекциях. 7. Рассказать статическое уравновешивание вращающихся масс в параллельных плоскостях. 8. Рассказать динамическое уравновешивание вращающихся масс в параллельных плоскостях.
СОДЕРЖАНИЕ 1. Технические данные установки ТММ*35А 3 2. Устройство и работа установки ТММ*35А 3 3. Порядок выполнения лабораторной работы 4 4. Методические указания по выполнению работы6 5. Примерные вопросы к защите лабораторной работы 12 |



 (4.3)
(4.3) .
. ¹ 0, то уравнение (1) примет вид:
¹ 0, то уравнение (1) примет вид: . (4.4)
. (4.4) имеет такое же направление, как и радиус-вектор центра тяжести, а тот в свою очередь направлен в ту же сторону, что и центробежная сила инерции Fи. Поэтому уравнение (4.4) легко решается построением векторного уравнения. Для этого считается масштабный коэффициент mGr
имеет такое же направление, как и радиус-вектор центра тяжести, а тот в свою очередь направлен в ту же сторону, что и центробежная сила инерции Fи. Поэтому уравнение (4.4) легко решается построением векторного уравнения. Для этого считается масштабный коэффициент mGr (4.5)
(4.5)


 mGr = (Hм).
mGr = (Hм).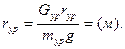 (4.6)
(4.6) перенести на схему механизма и замерить угол от вертикальной оси по часовой стрелке (рис. 2, а).
перенести на схему механизма и замерить угол от вертикальной оси по часовой стрелке (рис. 2, а). За начало координат выбираем точку «0» – точка пересечения оси ротора с плоскостью I уравновешивания. Условия равновесия имеют вид
За начало координат выбираем точку «0» – точка пересечения оси ротора с плоскостью I уравновешивания. Условия равновесия имеют вид
 (4.8)
(4.8)


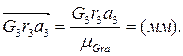

 a) РиII Риур
a) РиII Риур



 I 1 2 3 II Ри1
I 1 2 3 II Ри1

 mур mур
mур mур



 mII mII РиI
mII mII РиI



 mI m1 a1 m1
mI m1 a1 m1





 O mI
O mI

 а1 m3 m3 a2
а1 m3 m3 a2


 а2 m2 Ри3 a3 m2
а2 m2 Ри3 a3 m2 а3
а3 а Ри2
а Ри2
 mGrа = (Hм2).
mGrа = (Hм2).
 . Рассчитывается его действительное значение GIrI =
. Рассчитывается его действительное значение GIrI = 
 ,
,  перенести на схему механизма и замерить углы от вертикальной оси по часовой стрелке (рис. 2, а).
перенести на схему механизма и замерить углы от вертикальной оси по часовой стрелке (рис. 2, а).