 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Вероятностью появления случайного события А называется отношение числа исходов, благоприятствующих появлению события А, к общему числу равновозможных исходов. 12
Обозначается вероятность Р(А) и вычисляется по формуле:
где m – число благоприятствующих исходов, т.е. тех исходов, когда событие А наступает, n – число всех равновозможных исходов, т.е. всех исходов, каждый из которых не является более возможным, чем другой. Примеры. 1) При бросании игрального кубика выпало четное количество очков. Найти вероятность этого события. Решение. Событие А – выпадение четного количества очков. К равновозможным исходам этого события относятся все возможные варианты выпадения очков:1, 2, 3, 4, 5, 6 очков. Всего таких 6 вариантов, значит n=6. К благоприятствующим исходам относятся все те варианты, когда выпадет четное число: 2, 4, 6 очков, значит этих вариантов 3. Следовательно, 2) Чему равна вероятность достоверного и невозможного события? Решение. Для достоверного события, которое всегда происходит в опыте, любой равновозможный исход наступления этого события является и благоприятствующим. Значит m=n, следовательно, Р(А)=1. Невозможное событие никогда в данном опыте не происходит, значит благоприятствующих исходов его появления нет, т.е. Значит m=0, следовательно, Р(А)=0. Вывод 0 ≤ Р(А) ≤ 1. Задание 8.Решить следующие задачи: 1) В ящике 3 белых, 4 черных и 5 красных шаров. Наудачу вынимается один шар. Какова вероятность того, что это красный шар? Решение. Событие А – вынут один красный шар из 12 шаров. Всего шаров 12, значит один шар можно вынуть 2) Куб, все грани которого окрашены, распилен на 125 кубиков одинакового размера, которые затем тщательно перемешаны. Найти вероятность того, что наудачу извлеченные два кубика имеют три окрашенные грани. Решение. Событие А – извлечен кубик, имеющий три окрашенных грани. Всего равновозможных исходов Кубиков с тремя окрашенными гранями всего 8, т.к. всего вершин у куба было 8, и при распиливании этого куба кубики, расположенные в этих вершинах, будут иметь три окрашенные грани. Значит, благоприятствующим исходом будет любой из вариантов, когда два кубика будут выбраны среди этих 8. А таких вариантов будет 3) В мешке 6 одинаковых бочонков, на каждом из которых написан его порядковый номер. Все бочонки по одному наудачу извлекают. Найти вероятность того, что номера извлеченных бочонков появятся в возрастающем порядке. Решение. Событие А – номера извлеченных бочонков появились в порядке возрастания. Всего вариантов появления всех бочонков равно P6 =6!=720, т.е. n=720. Но только в одном варианте все номера будут расположены в возрастающем порядке, т.е. m=1. Значит, 4) В группе 5 юношей и 10 девушек. Среди них случайным образом распределяются три билета в театр. Найти вероятность того, что два билета окажутся у девушек, а один у юноши. Решение. Событие А – два билета у девушек, один у юноши. Три билета распределяются наудачу среди 15 человек. Значит, всего вариантов
12 |



 ,
, .
.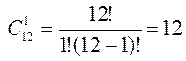 способами, т.е. n = 12. Красных шаров 5, значит именно красный шар можно вынуть
способами, т.е. n = 12. Красных шаров 5, значит именно красный шар можно вынуть 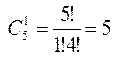 способами, т.е. m=5. Значит,
способами, т.е. m=5. Значит,  .
. . т.е. . n=7750.
. т.е. . n=7750. , т.е. m=28. Значит,
, т.е. m=28. Значит,  .
. .
. , т.е. n=455. Благоприятными будут исходы, когда двум девушкам из 10 достанутся билеты, это возможно сделать
, т.е. n=455. Благоприятными будут исходы, когда двум девушкам из 10 достанутся билеты, это возможно сделать  способами. Но при этом один билет должен достаться одному юноше из 5. это можно сделать
способами. Но при этом один билет должен достаться одному юноше из 5. это можно сделать 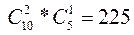 . Значит,
. Значит,  .
.