 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Методические указания к выполнению домашнего задания 12
Исходные данные для выполнения домашнего и лабораторного задания приведены в табл. 4.1. Таблица 4.1. Исходные данные
При выполнении домашнего задания следует воспользоваться описанными ниже соотношениями. 1. Сначала следует рассчитать погонную индуктивность исходя из известного соотношения для фазовой скорости 2. Волновое сопротивление 3. Длина линии 4. Частота резонанса четвертьволнового резонатора f0 расчитывается исходя из соотношений Следует отметить, что f0 равна минимальному значению частоты, на которой коэффициент передачи по напряжению длинной линии принимает максимальное значение, если RL > Rв , или минимальное значение, если RL < Rв. 5. Погонное сопротивление R п следует взять в 100 раз меньше реактивного сопротивления погонной индуктивности на частоте f0: R п = 2π f 0 L п / 100. 6. При воздействии одиночного импульса, напряжение на выходе линии без потерь в моменты времени t = t з + и t = 3t з + соответственно: u2(t з +) = u1(0+) (1 + ρ 2) и u2(3t з +) = u1(0 +) ρ 1 ρ 2 (1 + ρ 2), где u1(0+) = Е R в/(R i + R в) – напряжение на входе линии в момент времени t = 0+, ρ 1 = (R i – R в)/(R i + R в) и ρ 2 = (R L – R в)/(R L + R в) – коэффициенты отражения в начале и конце линии соответственно. 7. Добротность четвертьволнового резонатора рассчитывается двумя способами: а) по максимуму коэффициента передачи четвертьволнового отрезка линии QK = Kmax» 1 / (α l); б) по полосе пропускания четвертьволнового резонатора QП = f 0 / Пf » π / (4α l), где коэффициент ослабления α » Домашнее задание 1. В соответствии с вариантом работы рассчитайте минимальное и максимальное значения коэффициента передачи по напряжению линии без потерь при заданном сопротивлении нагрузки RL. Определите минимальные значения частот, на которых они наблюдаются. Постройте качественно график АЧХ. 2. Найдите выражения для АЧХ и ФЧХ коэффициента передачи по напряжению той же линии, согласованной с нагрузкой. Постройте графики АЧХ и ФЧХ в диапазоне от нуля до частоты, втрое превышающую найденную выше максимальную частоту. 3. Рассчитайте высоту импульсов напряжения на выходе той же линии при заданных сопротивлениях источника и нагрузки на интервале времени 4. Рассчитайте эквивалентную добротность и полосу пропускания четвертьволнового резонатора при заданных погонных параметрах линии. Лабораторное задание 1. Получите с помощью программы Multisim графики АЧХ и ФЧХ коэффициента передачи по напряжению линии без потерь при согласованной нагрузке и при заданной резистивной нагрузке, если ко входу линии подключен идеальный источник напряжения (Ri = 0). Проверьте точность расчетов домашнего задания. Проверьте в широком диапазоне частот, меняются ли максимальные и минимальные значения коэффициента передачи при отсутствии потерь. 2. Получите временные диаграммы напряжений на входе и выходе линии без потерь при ЭДС источника в виде прямоугольного импульса и заданных сопротивлениях источника и нагрузки. Получите еще 2 аналогичных графика: а) при заданном сопротивлении источника и согласованной нагрузке, б) при заданном сопротивлении нагрузки и согласованном с линией источнике. 3. Получите АЧХ и ФЧХ коэффициента передачи линии с потерями в режиме холостого хода на выходе (не следует удалять из схемы сопротивление RL, принять RL = 1Е9 Ом) и при подключении к линии идеального источника напряжения (так же не следует удалять сопротивление Ri,принятьRi= 1Е-3 Ом). Проверьте в широком диапазоне частот, меняются ли максимальные значения коэффициента передачи линии при наличии потерь. По первому максимуму АЧХ линии с потерями определите резонансную частоту f 0 , полосу пропускания П f и максимальное значение коэффициента передачи четвертьволнового резонатора Kmax. Определите добротность резонатора двумя способами: а) QK = Kmax, б) QП = f 0 / П f . 4. Получите временные диаграммы напряжений на входе и выходе линии с потерями при ЭДС источника в виде прямоугольного импульса и заданных сопротивлениях источника и нагрузки. Оцените искажения прямоугольного импульса (увеличение длительности задержанного импульса, длительность фронта и скол вершины) при использовании многозвенной модели. Контрольные вопросы 1. Чем принципиально отличаются уравнения электрического равновесия для мгновенных значений токов и напряжений цепей с сосредоточенными и распределенными параметрами? 2. Запишите общее решение телеграфных уравнений для комплексных амплитуд напряжений. Как называются слагаемые решения? 3. Сколько первичных параметров описывают однородную длинную линию? Как они называются, какова их размерность и физический смысл? 4. Какой физический смысл и размерность имеют характеристические (вторичные) параметры длинной линии? 5. Приведите классификацию длинных линий. Какие устройства моделирует каждый класс линий? 6. Чем отличаются однородная и неоднородная линии? 7. Как определяются коэффициент ослабления и коэффициент фазы? Какие размерности они имеют? 8. При каких условиях в длинной линии устанавливается режим а) режим бегущих волн, б) режим стоячих волн, в) режим смешанных волн? 9. Что такое коэффициент бегущей волны? Какие значения он может принимать при различных режимах работы длинной линии? 10. Что называется коэффициентом отражения по напряжению в конце линии? Как этот коэффициент связан со значением сопротивления нагрузки? Что называется коэффициентом отражения по напряжению в начале линии? 11. В каких случаях линию передачи следует считать «длинной»? Как выглядит простейшая схема замещения «короткой» линии передачи? 12. Какой длительности импульс напряжения, передаваемый по данной линии, можно считать «коротким»? 13. Что называется согласованием длинной линии с нагрузкой? 14. Каким образом можно заменить последовательный и параллельный колебательные контуры отрезком линии? 15. Что в теории длинных линий называется шлейфом? 16. Чему равна длина линии, если коэффициент распространения линии 17. Чему равен коэффициент затухания в линии длиной 60 км, если при согласованной нагрузке напряжение в начале линии U1 = 24 В, напряжение в конце линии U2 = 20 В? 18. Для линии без потерь построить график U(x′) и определить Кб, Rв, ρ2, если в конце линии наблюдается максимум напряжения Umax= 2 В. Минимум действующего значения напряжения Umin= 1,5 В, фазовая скорость vф = 2∙10 8м/с, частота гармонического воздействия f = 200 МГц, сопротивление нагрузки Rн = 100 Ом. 19. Длинная линия без потерь нагружена на емкостный элемент Сн = 10 пФ. Построить график U(x′), определить λ и Rв, если фазовая скорость vф = 3∙10 8м/с, частота гармонического воздействия f = 50 МГц, расстояние до ближайшего к концу линии узла напряжения x0' = 1 м. 20. Длинная линия без потерь нагружена на сопротивление Rн, в конце линии наблюдается максимум действующего значения напряжения. Кб = 0,9. Построить график U(x′), определить λ, f, Rн и ρ2, если фазовая скорость vф = 3∙10 8м/с, волновое сопротивление линии Rв = 50 Ом, расстояние до ближайшего к концу линии узла напряжения x0' = 1 м. 21. Линия без потерь нагружена на резистивный элемент Rн = 100 Ом. Погонные параметры линии L1 = 8∙10 – 7 Гн/м, С1 = 20∙10 – 12 Ф/м, длина линии l = 1 м. Рассчитать максимальное и минимальное значения АЧХ комплексного коэффициента передачи линии и построить график АЧХ. 22. Погонные параметры короткозамкнутого отрезка линии без потерь L1 = 10∙10 – 7 Гн/м, С1 = 16∙10 – 12 Ф/м. Постройте зависимость xк(l). Определите минимальную длину короткозамкнутого отрезка, если на частоте f = 200 МГц отрезок эквивалентен а) емкости Сэк = 100 пФ, б)индуктивности Lэк = 1,5 мкГн, в) последовательному контуру, г) параллельному контуру. 23. Для разомкнутого отрезка линии без потерь Rв = 75 Ом, vф = 3∙10 8 м/с. Постройте зависимость xх(l). Определите минимальную длину разомкнутого отрезка, если на частоте f = 100 МГц отрезок эквивалентен а) емкости Сэк = 100 пФ, б)индуктивности Lэк = 1,5 мкГн, в) последовательному контуру, г) параллельному контуру. 24. Линия без потерь нагружена на резистивный элемент Rн = 50 Ом. Волновое сопротивление линии Rв = 100 Ом. Рассчитайте комплексную входную проводимость линии, если длина линии а) l = λ/8; б) l = 3λ/8. 25. Длинная линия без потерь (Rв = 100 Ом, vф = 3∙108, l = 3 м) подключена к источнику напряжения в виде одиночного прямоугольного импульса (высота импульса E = 1 В, длительность импульса tи = t0 /5, внутреннее сопротивление источника Ri = 50 Ом). Рассчитать и построить график зависимости напряжения на выходе линии от времени (t
Для выполнения домашнего задания и подготовки к защите данной лабораторной работы необходимо изучить подраздел 4.2 данного руководства, повторить материал учебника [1, стр. 462 – 491] и задачника [2, № 8.1, 8.5, 8.9, 8.11, 8.16, 8.17, 8.31, 8.39, 8.41].
12 |
.
.
.
.
.
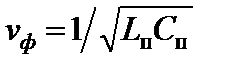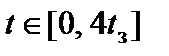, где tз – время задержки. Высоту импульса источника ЭДС принять E = 1 В, длительность импульса tи = tз / 4.
км – 1, постоянная ослаблении A = 0,9 Нп?
[0, 4t0+tи]), если сопротивление нагрузки а) Rн = 200 Ом; б) Rн = 50 Ом; в) Rн = 100 Ом; г) Rн = 0 Ом; д) Rн → ∞.