 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Описание исследуемых цепей 12
НЕЛИНЕЙНЫЕ РЕЗИСТИВНЫЕ ЦЕПИ Цель работы. Изучение методов графического анализа, аппроксимации характеристик и расчета гармонических составляющих отклика нелинейных резистивных цепей. Описание исследуемых цепей В работе исследуется две цепи – цепь (а) и цепь (б), схемы которых приведены на рис 3.1. Схема исследуемой цепи быстрее всего может быть получена путем преобразования (и переименования) схемы на рис. 1.5 (файл D.ms10). Исследуемые цепи содержат следующие элементы: V1– независимый источник гармонического напряжения; D1 –диод; R1 и R2 – резистивные элементы. Параметры элементов указаны в табл. 3.1. Рис. 3.1. Схемы нелинейных цепей Таблица 3.1 Параметры элементов нелинейных цепей
Методические указания к выполнению домашнего задания 3.2.1. Графоаналитический метод анализа нелинейных цепей Рассмотрим метод определения передаточных характеристик исследуемых цепей с помощью уравнений электрического равновесия и графических построений. Передаточная характеристика нелинейной цепи – это зависимость выходного напряжения цепи от входного напряжения u 2 = f (u 1) (для цепей, приведенных на рис. 3.1, u2 = uR2, u1 = uV1). Основная система уравнений электрического равновесия (ОСУ) цепи (а) имеет вид:
Исключив из ОСУ мгновенные значения токов, получим уравнения напряжений ветвей цепи (а):
Далее с помощью среды MATHCAD можно составить программу расчета передаточной характеристики цепи (а) (рис. 3.2)*.
Рис. 3.2. Программа расчета и график зависимости u 2 = f (u 1) цепи (а) Из ОСУ цепи (б) можно получить уравнения напряжений ветвей этой цепи:
и затем составить программу расчета передаточной характеристики цепи (б) (рис. 3.3).
Рис. 3.3. Программа расчета и график зависимости u 2 = f (u 1) цепи (б) 3.2.2. Аппроксимация табличной зависимости Для аппроксимации зависимости u2 = f (u1) сначала необходимо получить таблицу значений {u1 k , u2 k}, k = 1, 2, ..., N (N – количество точек). Значения {u1 k , u2 k} необходимо определять из графика передаточной характеристики с тремя-четырьмя точными значащими цифрами (см. рис. 3.2 или рис. 3.3). Коэффициенты аппроксимирующей функции (полинома) определяют методом наименьших квадратов (МНК) или методом выбранных точек (МВТ) с помощью приведенных ниже программ на языке MATHCAD. Графики экспериментальных и аппроксимирующих функций приведены на рис. 3.4. Программа аппроксимации табличной зависимости
Метод наименьших квадратов Начальные (приближенные) значения коэффициентов аппроксимирующего полинома:
Сумма квадратов абсолютных погрешностей в k-й точке:
Результаты минимизации:
Аппроксимирующий полином для МНК:
Максимальная абсолютная погрешность аппроксимации для МНК:
Метод выбранных точек
Решение СЛАУ:
Аппроксимирующий полином для МВТ:
Максимальная абсолютная погрешность аппроксимации для МВТ:
Рис. 3.4. Передаточная характеристика нелинейного четырехполюсника: Домашнее задание 1. Постройте график передаточной характеристики исследуемой цепи u 2 = f (u 1) при – 1,5 В ≤ u 1 ≤ 1,5 В, используя графоаналитический метод анализа нелинейных резистивных цепей. 2. Используя полученную в п. 1 зависимость u 2 = f (u 1), постройте график u 2 (t) при u 1 (t) = 1,5sin(2π∙1000t) В. 3. Аппроксимируйте рассчитанную в п. 1 зависимость u 2 = f (u 1) в диапазоне – 1,5 В ≤ u 1 ≤ 1,5 В степенным полиномом третьего порядка u 2 = a 0 + a 1 u 1 + a 2 u 12 + a 3 u 13 методом наименьших квадратов или выбранных точек. Найдите максимальную по модулю абсолютную ошибку аппроксимации. Постройте графики исходной зависимости u 2 = f (u 1) и аппроксимирующей функции на одном рисунке. 4. Используя найденные параметры аппроксимации a 0, a 1, a 2, a 3 , определите постоянную составляющую и амплитуды первых трех гармоник выходного напряжения u 2 (t) при максимальной для выбранного диапазона амплитуде входного гармонического напряжения(Um ВХ = 1,5 В). 5. Определите амплитуды гармонических составляющих u 2 (t) с разностной и суммарной частотами при подаче на вход цепи суммы двух гармонических колебаний с разными частотами, амплитуды которых равны половине амплитуды Um Вх , заданной в предыдущем пункте (Um ВХ 1 = Um ВХ 2 = 0,75 В). Лабораторное задание 1. С помощью программы Multisim получите передаточную кривую u 2 = f (u 1) заданной цепи (DC Sweep analysis), выбрав в качестве анализируемой функции напряжение u2 при – 1,5 В ≤ u1 ≤ + 1,5 В. 2. Получите отклик u2 (t) для трех амплитуд гармонического воздействия: 0,15; 1,5 и 15 В, выполнив анализ заданной цепи во временной области (Transient analysis). Амплитуды воздействия устанавливаются поочередно (параметр Voltage Pk источникагармонического напряжения V1)и при каждой амплитуде выполняется временной анализ. Остальные параметры источника V1следующие: постоянная составляющая Voltage Offset = 0 В; частота Frequency = 1 кГц; начальная фаза Phase= 0°. 3. С помощью гармонического анализа заданной цепи (Fourier Analysis) определите те же величины, что и в п. 4 домашнего задания. Частота воздействия равна 1 кГц. 4. Подключите к заданной цепи второй источник гармонического напряжения последовательно с первым источником и с помощью гармонического анализа полученной цепи определите те же величины, что и в п. 5 домашнего задания. Частота первого воздействия f 1 = 1 кГц, второго f 2 = 800 Гц В диалоговом окне Fourier Analysis установите основную частоту Fundamental frequency= 200 Гц и число определяемых гармоник Number of harmonics = 12. 5. Повторите п. 3 и п. 4 лабораторного задания при уменьшении амплитуды напряжения на входе в 10 раз. Контрольные вопросы 1. Какая характеристика сопротивления называется основной? 2. Какие резистивные элементы называются линейными, нелинейными? 3. Как классифицируются нелинейные резистивные элементы по виду основной характеристики? 4. Что называется статическим сопротивлением? 5. Что называется дифференциальным сопротивлением? 6. Какие резистивные элементы называются элементами с отрицательным сопротивлением? На какие две группы разделяют эти элементы? 7. Каким образом можно графически найти отклик u2(t) при входном напряжении u1(t) произвольной формы? 8. Какие нелинейные элементы называются управляемыми? Приведите примеры управляемых нелинейных элементов. 9. Каким идеализированным элементом можно заменить нелинейный резистивный элемент? 10. Какая цепь называется нелинейной? Чем отличаются математические модели линейных и нелинейных цепей? 11. Что называется гармоникой тока (напряжения)? 12. Какие гармоники содержит отклик, если нелинейная характеристика аппроксимируется: а) степенным полиномом n-го порядка; б) четным полиномом; в) нечетным полиномом; г) экспонентой? 13. Если нелинейная характеристика описывается полиномом четвертого порядка, то обязательно ли отклик содержит вторую гармонику? 14. Что называется аппроксимацией? 15. Какими методами определяются параметры аппроксимации? Приведите примеры аппроксимирующих функций. 16. Могут ли совпасть аппроксимирующие одну и ту же зависимость полиномы, полученные методами выбранных точек и наименьших квадратов? 17. Какой режим работы нелинейной цепи называется «режимом малого сигнала»? 18. Как определить экспериментально, в режиме большого или малого сигнала находится анализируемая цепь при гармоническом воздействии? 19. Всегда ли гармонические составляющие отклика являются гармониками? 20. Какие частоты имеют комбинационные составляющие отклика при аппроксимации передаточной зависимости u2 = f (u1) полиномом третьего порядка? 21. Определите графически напряжение на входе цепи состоящей из двух параллельно-соединенных нелинейных сопротивлений, ВАХ которых приведены на рис. 3.5, если ток на входе цепи I_= 1,5 мА. 22. Определите графически ток на входе цепи состоящей из двух последовательно-соединенных нелинейных сопротивлений, ВАХ которых приведены на рис. 3.5, если напряжение на входе цепи U_= 3 мА. Рис. 3.5. ВАХ нелинейных резистивных элементов 23. Постройте график ВАХ цепи состоящей из двух параллельно-соединенных нелинейных сопротивлений, ВАХ которых приведены на рис. 3.5. 24. Постройте график ВАХ цепи состоящей из двух последовательно-соединенных нелинейных сопротивлений, ВАХ которых приведены на рис. 3.5. 25. Для нелинейных сопротивлений, ВАХ которых приведены на рис. 3.6, построить графики зависимостей Rст(u) и Rдиф(u). 26. Для нелинейных сопротивлений, ВАХ которых приведены на рис. 3.6, построить графики зависимостей Gст(u) и Gдиф(u). Рис. 3.6. Кусочно-линейные ВАХ 27. ВАХ нелинейного сопротивления имеет вид i(u) = 0,1 +0,5 u + u2, мА. Постройте графики зависимостей i(u) и Gдиф(u) при 28. ВАХ нелинейного сопротивления имеет вид u(i) = 1 +2 i +4 i2 В. Постройте графики зависимостей i(u) и Rдиф(u) при 29. ВАХ нелинейного сопротивления имеет вид i =0,1 + u + 0,2 u2, мА. Определите амплитуды и частоты гармонических составляющих тока, если приложенное к нелинейному сопротивлению напряжение u = 2 sin (2π∙100t), В. 30. ВАХ нелинейного сопротивления имеет вид i = 0,5 u2, мА. Определите амплитуды и частоты гармонических составляющих тока, если приложенное к нелинейному сопротивлению напряжение u = 2 sin (2π∙100t) + cos (2π∙300t) , В.
Для выполнения домашнего задания и подготовки к защите данной лабораторной работы необходимо изучить подраздел 3.2 данного руководства, повторить материал учебника [1, стр. 275 – 305] и задачника [2, № 5.20, 5.22, 5.35]. ДЛИННАЯ ЛИНИЯ Цель работы. Изучение частотных характеристик и переходных процессов в длинной линии средствами симулятора Multisim. Описание исследуемых цепей В работе исследуются две цепи. В первой из них, показанной на рис. 4.1, длинная линия моделируется идеальным элементом задержки W1 с параметрами Z0 – волновое сопротивление и TD – время задержки. Эта модель полностью эквивалентна отрезку однородной линии без потерь с соответствующими параметрами. Рис. 4.1. Длинная линия без потерь с подключенным источником энергии и нагрузкой Схема на рис. 4.1 содержит: V1 – независимый источник напряжения в виде прямоугольного импульса, описание которого при длительностях импульса 1 нс и фронтов 1 пс приведено на рис. 4.2;
Рис. 4.2. Описание кусочно-линейного напряжения в виде импульса, Ri и RL – резистивные элементы, моделирующие внутреннее сопротивление источника и нагрузку; W1 – модель однородной длинной линии без потерь, для ввода которой необходимо осуществить следующую последовательность действий: Components → Вторая цепь, моделирующая длинную линию с потерями, имеет вид многозвенной цепи, состоящей из 32-х секций. К многозвенной цепи подключается источник напряжения V1с внутренним сопротивлением Ri и нагрузкаRL, параметры этих элементов такие же, как и для линии без потерь. На рис 4.3, а приведена схема первых трех звеньев линии, подключенных к источнику, а на рис 4.3, б – последних трех звеньев, с подключенной нагрузкой. Рис. 4.3. Схема замещения длинной линии с потерями (а – начало линии с источником V1, Ri, б – конец линии с нагрузкой RL) Параметры элементов многозвенной цепи следующие: L k = L п l / N, R k = R п l / N, C k = C п l / N, за исключением C 0 = C 32 = C п l / (2N), где N = 32 – число звеньев, k – номер звена, l – длина линии, L п , C п , R п – погонные параметры. Длина линии, погонные параметры, время задержки линии, параметры источника и нагрузки выбираются в соответствии с заданным вариантом (подразд. 4.2). Для ввода схемы многозвенной цепи необходимо увеличить размер рабочей области поля ввода схемы следующим образом: Options → Sheet properties… → Workspace → Custom size → Width: 150 cm, Height: 20 cm. Вначале рекомендуется ввести первое звено и задать параметры его элементов L 1 , R 1, C 1 , затем скопировать это звено в буфер обмена и вставлять до получения 32-х звеньев, которые необходимо соединить в соответствии с рис. 4.3. Размещать элементы схемы рекомендуется в один ряд. 12 |








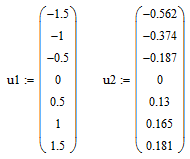













 и рассчитайте значения Gст и Gдиф при u = 2 В.
и рассчитайте значения Gст и Gдиф при u = 2 В. и рассчитайте значения Rст и Rдиф при i = 1 А.
и рассчитайте значения Rст и Rдиф при i = 1 А.
 Place miscellaneous →
Place miscellaneous →  .
.