 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Задания для аудиторной работы 12
Задание 1.1.Найти канонические разложения чисел Решение.
Задание 1.2.Найти НОД (627,399), воспользовавшись: а) алгоритмом Евклида; б) разложением чисел на простые множители. Решение. Применим алгоритм Евклида: 627 = 399 ∙ 1 + 228; 399 = 228 ∙ 1 + 171; 228 = 171 ∙ 1 + 57; 171 = 57∙ 3. Следовательно, НОД (627; 399) = 57. Найдем НОД (а, 627 = 3 ∙ 11∙ 19; 399 = 3 ∙ 7 ∙ 19. Следовательно, наибольшим общим делителем будет произведение одинаковых множителей, входящих как в одно, так и в другое разложения чисел НОД (627; 399) = 3 ∙ 19 = 57. Найдем НОД (а, 627 – 399 = 228; 399 – 228 = 171; 228 – 171 = 57; 171 – 57 = 114; 114 – 57 = 57; 57 – 57 = 0. Следовательно, НОД (627; 399) = 57. Задание 1.3.С помощью расширенного алгоритма Евклида найти целые числа Решение. Сначала найдем по алгоритму Евклида НОД (110, 48): 110 = 48 ∙ 2 + 14; 48 = 14 ∙ 3 + 6; 14 = 6 ∙ 2 + 2; 6 = 3 ∙ 2. Следовательно, НОД (110, 48) = 2. Теперь построим соотношение Безу для данных 110 = 48 ∙ 2 + 14; поэтому 14 = 110 + 48 ∙ (–2); 48 = 14 ∙ 3 + 6; поэтому 6 = 48 + 14 ∙ (–3); 14 = 6 ∙ 2 +2; поэтому 2 = 14 + 6 ∙ (–2). В это равенство подставим выше полученное выражение для 6 и приведем подобные относительно чисел 48 и 14. Итак 2 = 14 + 6 ∙ (–2) = 14 + (48 + 14 ∙ (–3))( –2) = 14 ∙ 7 + 48 ∙ (–2). В полученное выражение для НОД (110, 48) = 2 подставим вышеприведенное выражение числа 14. Получим окончательно 2 = 14 ∙ 7 + 48 ∙ (–2) = (110 + 48 ∙ (–2)) 7 + 48 ∙ (–2) = 110 ∙ 7 + 48 ∙ (–16) = 2. Задание 1.4. а) записать в двоичной системе счисления число 137. Решение. Проведем последовательные деления на 2:
_137 | 2 12 | _68 | 2 _17 68 | _34 | 2 16 0 34 | _17 | 2
1 8 | _4 | 2 0 4 | _2 | 2 0 2 | _1 | 2 0 0 | 0 1
Число записываем по остаткам деления на 2, но в обратном порядке: 137 = 100010012;
б) перевести число 100010012 в десятичную систему: 1 0 0 0 1 0 0 12 = (1 ∙ 27 + 0 ∙ 26 + 0 ∙ 25 ∙ 0 ∙ 24 + 1 ∙ 23 + 0 ∙ 22 + 0 ∙ 21 + 1 ∙ 20) = = 7 6 5 4 3 2 1 0. (27 +23 +1)10 = 128 + 8 +1 = 13710; в) перевести число 10000 в восьмеричную систему счисления:
_10000 | 8 8 | _1250 | 8 _20 8 | _156 | 8 16 _45 8 | _19 | 8 _40 40 _76 16 | _2 | 8 40 _50 72 3 0 | 0
1000010 = 234208.
Задание 1.5.Умножение и сложение в 16-ричной системе счисления. В 16-ричной системе счисления используются цифры и латинские буквы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, B, C, D, E, F. Здесь буква А – это число 10, буква В – 11, С – 12, D – 13, E – 14, F – 15. Для выполнения арифметических операций в 16-ричной системе построим таблицу 1.1 и таблицу 1.2.
Таблица 1.1 Сложение чисел в 16-ричной системе счисления
Таблица 1.2 Умножение чисел в 16-ричной системе счисления
Разберем пример сложения чисел непосредственно и с применением табл. 1.1.
Табл. 1.1 используется так: первое слагаемое (в данном примере
Таблицу сложения (см. таблицу 1.1) можно использовать и как таблицу для вычитания чисел:
6 – 8 (для вычитания берем единицу второго разряда и превращаем в 10 единиц первого, во втором разряде осталось 7 единиц); 10 + 6 – 8 = 16 – 8 = Е; 7 – 8 (для вычитания берем единицу третьего разряда, но так как записан 0, берем единицу четвертого разряда, превращаем ее в 10 единиц третьего разряда и единицу третьего – в 10 единиц второго; в четвертом разряде остались 2 единицы, в третьем – F единиц); 10 + 7 – 8 = 17 – 8 = F; F – 9 – 6; 2 – 8 (для вычитания единицу пятого разряда превращаем в 10 единиц четвертого); 10 + 2 – 8 = 12 – 8 = А. Для нахождения разности двух чисел по табл. 1.1 вычитаемое отыскивается в верхней строке, уменьшаемое – внутри таблицы в столбце, соответствующем вычитаемому, разность берется в крайнем левом столбце в соответствии с уменьшаемым. Здесь умножение выполнялось следующим образом:
Отобразим схему решения (используем таблицу 1.2):
Задание 1.6. а) найти остаток от деления 2100 на 3. Решение.1-й способ: 2 делится на 3 с остатком 2, 22 делится на 3 с остатком 1. При дальнейшем возведении двойки в степень остатки от деления будут чередоваться: 2, 1, 2, 1, 2 … . Значит, в силу четности степени 100 остаток от деления требуемого числа на 3 будет равен 1.2-й способ – методом сравнений, по аналогии с примером 1.6: б) найти остаток от деления Решение. Заменим каждое число на его остаток от деления на 7:
_1989 | 7 _1990 | 7 1991 = 7 ∙ 284 + 3; 14 | 284 14 | 284 _58 _59 1992 = 7 ∙ 284 + 4. 5656 _29 _30 2828 1 2 1 ∙ 2 ∙ 3 + 43 = 6 + 64 = 70. 70 : 7 = 10. Следовательно, остаток равен нулю; в) найти остаток от деления Решение. Заменим 9 на его остаток 1 от деления на 8. Имеем г) найти остаток от деления Решение. 3 делится на 7 с остатком 3. 12 |





 Следовательно, 627 = 3∙11∙19, 399 = 3∙7∙19.
Следовательно, 627 = 3∙11∙19, 399 = 3∙7∙19. ), воспользовавшись разложением на простые множители чисел
), воспользовавшись разложением на простые множители чисел  и
и  полученным в решении задания 1.1:
полученным в решении задания 1.1: , удовлетворяющие соотношению Безу:
, удовлетворяющие соотношению Безу:  для целых чисел
для целых чисел 
 :
:
 1 0 16 | _8 | 2
1 0 16 | _8 | 2 0 48 4 2
0 48 4 2
 (2 пишем, 1 переносим в старший разряд);
(2 пишем, 1 переносим в старший разряд); (
(  пишем в сумме);
пишем в сумме); (1 пишем, 1 переносим в старший разряд);
(1 пишем, 1 переносим в старший разряд); (4 пишем, 1 переносим в старший разряд);
(4 пишем, 1 переносим в старший разряд);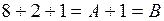 (
(  пишем).
пишем). или
или  ) отыскивается в строке таблицы сверху; второе слагаемое
) отыскивается в строке таблицы сверху; второе слагаемое
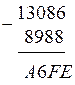
 (0 пишем, 2 переносим в старший разряд).
(0 пишем, 2 переносим в старший разряд). (А пишем, 4 – в старший разряд);
(А пишем, 4 – в старший разряд); (3 пишем, С – пишем);
(3 пишем, С – пишем); (С пишем, 1 – в старший разряд);
(С пишем, 1 – в старший разряд); (0 пишем, 4 – в старший разряд);
(0 пишем, 4 – в старший разряд); (3 пишем, 5 пишем);
(3 пишем, 5 пишем); (С пишем);
(С пишем); (B пишем, 1 – в старший разряд);
(B пишем, 1 – в старший разряд); (1 пишем, 6 пишем).
(1 пишем, 6 пишем). ;
; на 7.
на 7. на 8.
на 8. . Значит, остаток от деления
. Значит, остаток от деления  на 8 равен 1;
на 8 равен 1; на 7.
на 7. делится на 7 с остатком 2. Далее достаточно на 3 умножить только остаток и сделать выводы.
делится на 7 с остатком 2. Далее достаточно на 3 умножить только остаток и сделать выводы.  делится на 7 с остатком 6,
делится на 7 с остатком 6,  делится на 7 с остатком 4,
делится на 7 с остатком 4, 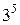 делится на 7 с остатком 5,
делится на 7 с остатком 5,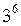 делится на 7 с остатком 1,
делится на 7 с остатком 1,  делится на 7 с остатком 3. Получили один из предыдущих остатков, значит «зациклились». Число
делится на 7 с остатком 3. Получили один из предыдущих остатков, значит «зациклились». Число  дает тот же остаток деления на 7, что и 31. Значит, длина цикла равна 6.
дает тот же остаток деления на 7, что и 31. Значит, длина цикла равна 6.  . Число
. Число  дает тот же остаток от деления на 7, что и
дает тот же остаток от деления на 7, что и