 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Основные свойства сравнений. 12
Теория чисел Теоретические сведения
Ниже рассматриваются N – множество натуральных чисел, Z – множество целых чисел. Множество целых чисел Z – счетное, состоит из элементов 1) ассоциативность: коммутативность: 2) существует нейтральный элемент – 0 или 1 соответственно: 3) 4) для каждого целого Теорема 1.1 (о делении с остатком). Для любых целых чисел a и b, В этом равенстве Следствие. Пусть
Такое равенство записывают сокращенно Лемма 1.1. Если в равенстве Определение 1.1.Если целые числа В дальнейшем речь идет только о положительных целых делителях. Определение 1.2.Максимальный из общих делителей целых чисел Теорема 1.2. Если Теорема 1.2 позволила Евклиду (примерно 2300 лет тому назад) обосновать следующий факт. Теорема 1.3. Наибольший общий делитель целых чисел a и b
…………………
Теорема 1.3 формулирует алгоритм Евклида для нахождения наибольшего общего делителя целых чисел. Его вариантом является следующий (второй способ вычисления наибольшего общего делителя по алгоритму Евклида): вычисляем последовательно разности Пример 1.1. С помощью алгоритма Евклида найти НОД (72, 26). Решение. В соответствии с теоремой 1.2 Теорема 1.4. Если Пример 1.2. Из примера 1.1 следует, что
Такой способ получения соотношения Безу для конкретных целых чисел называется расширенным алгоритмом Евклида. Он состоит из двух этапов: собственно алгоритма Евклида – прогонки вниз и прогонки вверх – и последовательного выражения остатков в каждом из шагов предыдущего этапа (с соответствующим приведением подобных на каждом шаге). Определение 1.3. Натуральное число Теорема 1.5. Всякое натуральное число Заметим, что из соотношения Теорема 1.6 (теорема Евклида). Простых чисел бесконечно много. Значение простых чисел в том, что они по теореме 1.5 являются составными кирпичиками всех натуральных чисел. Определение 1.4. Целые числа Теорема 1.7 (критерий взаимной простоты целых чисел). Целые числа a и b взаимно просты тогда и только тогда, когда существуют такие целые u и v, что выполняется равенство Следствие. Важным в теории чисел и ее приложениях является следующее свойство взаимно простых целых чисел. Лемма 1.2. Пусть произведение целых чисел Теорема 1.8 (основная теорема арифметики). Всякое целое число
Если в этом равенстве собрать одинаковые множители, то получим каноническое разложение целого числа Пример 1.3. Приведем примеры канонических разложений целых чисел: Теорема 1.9.Пусть 1) 2) 3) Определение 1.5.Целые числа Пример 1.4. –5 Пример 1.5. Если Основные свойства сравнений. 1. Пусть 2. Сравнения можно почленно складывать и вычитать: если 3. Сравнения можно почленно перемножать: если 4.Сравнения можно почленно возводить в любую натуральную степень: если 5. Если в сравнении 6. Сравнение можно сократить на общий множитель, взаимно простой с модулем: если 7. Сравнение можно умножить на любой целый множитель: если 8. Рефлексивность: 9. Симметричность: если 10. Транзитивность: если Теорема 1.10 (малая теорема Ферма). Пусть Теория сравнений и малая теорема Ферма позволяют быстро находить остаток от деления большого числа на простое число. Пример 1.6. Найдем остаток от деления Решение. 39 не делится на простое число 31. Поэтому
Таким образом, остаток от деления 12 |



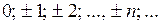 . На нем определены две алгебраические операции – сложение и умножение. Эти операции обладают следующими свойствами (для любых
. На нем определены две алгебраические операции – сложение и умножение. Эти операции обладают следующими свойствами (для любых  ):
): ;
;  ;
; ;
;  ;
;
 – закон дистрибутивности;
– закон дистрибутивности; существует единственное противоположное целое
существует единственное противоположное целое  такое, что
такое, что  .
. , существуют единственные целые числа q и
, существуют единственные целые числа q и  ,
,  , такие, что
, такие, что  .
. – частным (неполным частным – при
– частным (неполным частным – при  ) от деления
) от деления  на
на  величины
величины  натуральное число,
натуральное число,  Для всякого целого числа
Для всякого целого числа 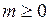 с условием
с условием  существуют единственные целые
существуют единственные целые  такие, что
такие, что
 или
или  (если
(если  Кажется естественной привычная десятичная позиционная система записи целых чисел
Кажется естественной привычная десятичная позиционная система записи целых чисел  . В различных ситуациях более удобными оказываются другие основания. Например, во всех компьютерах на микроуровне вычисления проводятся в двоичной системе счисления. Для перехода к ней с десятичной применяют промежуточную 16-ричную систему счисления.
. В различных ситуациях более удобными оказываются другие основания. Например, во всех компьютерах на микроуровне вычисления проводятся в двоичной системе счисления. Для перехода к ней с десятичной применяют промежуточную 16-ричную систему счисления. все слагаемые – целые числа и все, кроме может быть одного, делятся на целое
все слагаемые – целые числа и все, кроме может быть одного, делятся на целое  , то и это исключенное слагаемое также делится на
, то и это исключенное слагаемое также делится на 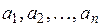 делятся на целое
делятся на целое  называется их наибольшим общим делителем и обозначается
называется их наибольшим общим делителем и обозначается , то
, то 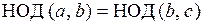 .
. равен последнему отличному от нуля остатку цепочки равенств:
равен последнему отличному от нуля остатку цепочки равенств: ;
; ;
; т. е.
т. е.  .
. .
. до получения последней ненулевой разности, которая и совпадает с
до получения последней ненулевой разности, которая и совпадает с  .
. ;
;  ;
;  ;
;  . Следовательно, НОД (72, 26) = 2.
. Следовательно, НОД (72, 26) = 2. , то существуют такие целые
, то существуют такие целые  и v, что выполняется следующее соотношение (соотношение Безу):
и v, что выполняется следующее соотношение (соотношение Безу):  .
.
 называется простым, если оно делится только на 1 и на себя.
называется простым, если оно делится только на 1 и на себя. либо является простым числом, либо имеет простой делитель.
либо является простым числом, либо имеет простой делитель.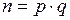 натуральных чисел, больших единицы, следует, что либо
натуральных чисел, больших единицы, следует, что либо  , либо
, либо  . Легко видеть, что наименьший натуральный делитель
. Легко видеть, что наименьший натуральный делитель  , носит название «решета Эратосфена». К настоящему времени разработан достаточно большой цикл алгоритмов проверки числа на простоту.
, носит название «решета Эратосфена». К настоящему времени разработан достаточно большой цикл алгоритмов проверки числа на простоту. .
. .
. тогда и только тогда, когда
тогда и только тогда, когда 

 делится на целое число
делится на целое число  и
и  . Тогда
. Тогда  .
. .
.
 – натуральное число,
– натуральное число,  Для любых целых чисел
Для любых целых чисел  следующие условия равносильны:
следующие условия равносильны:
 делится на
делится на  т. е.
т. е.  для подходящего целого
для подходящего целого 
 для некоторого целого
для некоторого целого 
 если они удовлетворяют одному из условий теоремы 1.9. Этот факт обозначают формулой
если они удовлетворяют одному из условий теоремы 1.9. Этот факт обозначают формулой  или
или  и называют данную формулу сравнением.
и называют данную формулу сравнением. 7(mod 4)
7(mod 4)  то
то  всякое целое число сравнимо по модулю
всякое целое число сравнимо по модулю  Это следует из определения 1.5 и второго условия теоремы 1.9. Ведь
Это следует из определения 1.5 и второго условия теоремы 1.9. Ведь  делится на
делится на  Тогда
Тогда  для всякого целого числа
для всякого целого числа  то есть к обеим частям сравнения можно добавить (или вычесть из обеих частей) одно и то же число.
то есть к обеим частям сравнения можно добавить (или вычесть из обеих частей) одно и то же число.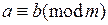 ,
,  то
то 



 то
то 
 имеют общий множитель
имеют общий множитель  то на него сравнение можно сократить
то на него сравнение можно сократить  .
. ,
,  , то из сравнения
, то из сравнения  следует сравнимость
следует сравнимость  и
и  по модулю
по модулю  .
. для всякого целого числа
для всякого целого числа 
 для любого целого
для любого целого 
 то
то 
 и
и 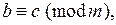 то
то 
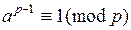 .
. на 31.
на 31.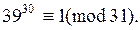 Следовательно,
Следовательно,  Далее
Далее  Поэтому в силу свойства 4 сравнений
Поэтому в силу свойства 4 сравнений  Двоичная запись 29 = 11101. Следовательно, для любого натурального
Двоичная запись 29 = 11101. Следовательно, для любого натурального 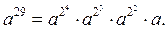
 Поэтому
Поэтому  Тогда
Тогда 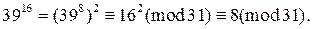 Следовательно,
Следовательно,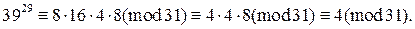
 на 31 равен 4.
на 31 равен 4.