 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Примеры программной реализации рассмотренных методов 12
Лабораторная работа №2 «Вычисление определенных интегралов и определенных интегралов специального вида.» Волгоград 2012
СОДЕРЖАНИЕ 1. Цель работы.. 4 2. Краткие теоретические сведения. 4 3. Примеры программной реализации рассмотренных методов. 12 4. Задание к выполнению... 18 5. Контрольные вопросы.. 19 6. Рекомендуемая литература.. 19
1.Цель работы: научиться осуществлять приближенное численное вычисление определенного интеграла и ознакомиться с приемами вычисления несобственных интегралов путем написания специализированных программ на языке высокого уровня. Общие теоретические сведения. Задача численного интегрирования функции заключается в вычислении определенного интеграла на основании ряда значений подынтегральной функции. Численное вычисление однократного интеграла называется механической квадратурой. Мы будем рассматривать способы приближенного вычисления определенных интегралов
основанные на замене интеграла конечной суммой:
где Сk- числовые коэффициенты, а xk Î [a, b], k = 0, 1, …, n. Приближенное равенство
называется квадратурной формулой, а xk – узлами квадратурной формулы. Погрешность квадратурной формулы определяется соотношением
В общем случае погрешность квадратурной формулы (5.4) зависит как от выбора коэффициентов Ск , так и от расположения узлов хк. Введем на отрезке [a, b] равномерную сетку с шагом h, тогда xi = a + ih, где (i = 0, 1, ..., n;h·n = b-a). Теперь выражение (5.1) можно представить в виде суммы интегралов по частичным отрезкам:
Таким образом, для построения формулы численного интегрирования на отрезке [a, b] достаточно построить квадратурную формулу на частичном отрезке [xi-1, xi] и воспользоваться формулой (5.5). Формула прямоугольников На частичном отрезке [xi-1, xi] заменим подынтегральную функцию полиномом Лагранжа нулевого порядка, построенным в одной точке. Естественно в качестве этой точки выбрать среднюю: xi-0.5 = xi - 0.5h. Тогда получим формулу
Подставив (5.6) в (5.5), получим составную формулу средних прямоугольников:
Графическая иллюстрация метода средних прямоугольников представлена на рис. 5.1.
Рис. 5.1. Интегрирование методом средних прямоугольников Погрешность формулы (5.7) определяется выражением
Здесь Замечание. Формулу (5.7) можно представить в ином виде:
Эти формулы в выражении (5.9) называются формулой левых и правых прямоугольников соответственно. Графически метод левых и правых прямоугольников представлен на рис. 5.2.
а) б) Рис. 5.2. Метод левых (а) и правых (б) прямоугольников Однако из-за нарушения симметрии в формулах (5.9) их погрешность значительно больше, чем в методе средних прямоугольников и ~O(h). Формула трапеций Если на частичном отрезке подынтегральную функцию заменить полиномом Лагранжа первой степени, то есть
тогда искомый интеграл запишется следующим образом:
После подстановки выражения (5.11) в (5.5) составная формула трапеций примет вид
Графически метод трапеций представлен на рис. 5.3.
Рис. 5.3. Метод трапеций Погрешность формулы (5.12) определяется выражением:
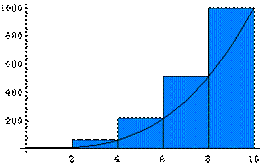
Таким образом, погрешность метода трапеций Ψ ~ O(h²), но она в два раза больше, чем для формулы средних прямоугольников. Формула Симпсона В этом методе предлагается подынтегральную функцию на частичном отрезке аппроксимировать параболой, проходящей через точки (xj, f(xj)), где j = i-1; i-0.5; i, то есть подынтегральную функцию аппроксимируем интерполяционным многочленом Лагранжа второй степени:
Проведя интегрирование, получим:
Это и есть формула Симпсона или формула парабол. На отрезке [a, b] формула Симпсона примет вид
Графическое представление метода Симпсона показано на рис. 5.4.
Рис. 5.4. Метод Симпсона Избавимся в выражении (5.16) от дробных индексов, переобозначив переменные:
Тогда формула Симпсона примет вид
Погрешность формулы (5.18) оценивается следующим выражением:
где h·n = b - a, Замечание. Следует отметить, что в формуле Симпсона отрезок интегрирования обязательно разбивается на четное число интервалов. Таким образом, определенный интеграл Метод прямоугольников - простейший способ численного интегрирования, при котором функция y=f(x) заменяется интерполяционным многочленом нулевого порядка ( горизонтальным отрезком). Для повышения точности интегрирования отрезок [a, b] разбивается на m частей и формула площади прямоугольника применяется к каждому отрезку. Таким образом, исходная функция y=f(x) аппроксимируется ломаной, состоящей из горизонтальных и вертикальных отрезков и обобщенная формула численного интегрирования имеет вид:
Вследствие низкой точности данный метод практически не применяется. Для повышения точности используется модифицированный метод прямоугольников, который базируется на представлении f(x) ординатами, смещенными на величину 0,5h, где h=(b-a)/m . Таким образом, получаем
где f’’(x) - значение второй производной в точке x=x, , где она максимальна. Метод трапеций заключается в линейной аппроксимации y=f(x) на отрезке [a, b]. Для уменьшения погрешности отрезок также разбивается на m частей длины h=(b-a)/m . С учетом суммирования смежных ординат внутри отрезка обобщенная формула имеет вид
В связи с легкостью программной реализации примеры программ для этих методов не приводятся. Метод Ньютона - Котеса (1686-1722)основан на интерполяции функции в n промежутках полиномом Лагранжа.
В общем случае f(xi) должна задаваться (n+1) ординатами. Формулы интегрирования увеличивают точность с ростом степени многочлена. При n=1 получаем метод трапеций. Частным случаем метода Ньютона- Котеса является также метод Симпсона (парабол), получающийся при n=2. Для трех узлов формула имеет вид:
При разбиении отрезка [a, b] на m равных отрезков получаем обобщенную или составную формулу Симпсона:
Выражение для остаточного члена показывает, что точность этого метода очень высока, что объясняет преимущественное применение этого метода при отыскании определенных интегралов. При повышении степени полинома до n=3 увеличивается точность вычислений, что приводит к интегрированию по формуле Бодэ.
При использовании полинома Лагранжа пятого порядка реализуется интегрирование по методу Уэддля.
Приведенные ранее методы интегрирования имеют равномерное расположение абсцисс xi, для которых вычисляются y=f(x) . При этом крайние значения xi равны a и b за исключением модифицированного метода прямоугольников. Однако равномерный шаг по оси абсцисс не является обязательным условием для численного определения интеграла. Метод Чебышева основан на вычислении значения определенного интеграла по формуле при неравномерном расположении абсцисс.
Для n=3 абсциссы ti располагаются неравномерно и, соответственно, равны t1=-Ö2/2, t2=0, t3=Ö2/2. Переход от параметра t к переменной x осуществляется подстановкой:
Метод Гаусса основан на интерполяции y=f(x) полиномом Лагранжа, но абсциссы xi выбираются из условия минимума погрешности интерполяции. При этом интеграл с помощью предыдущей подстановки сводится к виду
Метод Гаусса обычно обеспечивает повышенную точность. Для n=3 A1=5/9, t1=--Ö(1/3), A2=8/9,t2=0, A3=5/9, t3=Ö(1/3). При этом погрешность равна:
Для дальнейшего повышения точности интегрирования отрезок [a,b] дробится на m частей. При численном интегрировании для обеспечения заданной погрешности требуется вычислять высшие производные от подынтегральной функции, что не всегда удобно. Поэтому на практике принято проводить интегрирование для ряда разбиений отрезка на m частей. Несобственный интеграл представляет собой обобщение классического понятия интеграла на случай неограниченных функций и функций, заданных на бесконечном интервале интегрирования. Определенный интеграл, как предел интегральных сумм, может существовать (т.е. иметь определенное конечное значение ) лишь для ограниченных функций, заданных на конечном интервале. Поэтому, если интервал интегрирования или подинтегральная функция не ограничены, для определения интеграла используется ещё один предельный переход. Если этот предел существует, то говорят, что несобственный интеграл сходится, в противном же случае интеграл является расходящимся. Таким образом, несобственными интегралами называются интегралы, у которых f(x)®µ на отрезке [a,b], либо f(a) ®µ или f(b) ®µ. Вычисление несобственных интегралов с f(x)®µ на концах отрезка может быть осуществлено методами Гаусса и Чебышева, так как у них узлы интерполяции не совпадают с пределами интегрирования. При этом наличие особенности влияет на точность интегрирования. Метод Ньютона-Котеса (в частности, метод Симпсона) удобно применять, если f(x0 )®µ при х0 принадлежащем интервалу (a,b). Равномерное расположение узлов интерполяции облегчает контроль за их расположением и позволяет исключить ситуацию когда xi=x0. Сходящиеся несобственные интегралы с бесконечными пределами интегрирования могут вычисляться с помощью специальных приемов. Так, интеграл вида
может вычисляться как обыкновенный при выборе промежуточного предела интегрирования b из условия
e - заданная погрешность интегрирования. Для обеспечения этого условия производится автоматическое увеличение предела интегрирование до тех пор пока на i-ой стадии разность между двумя значениями интеграла не станет меньше допустимой погрешности. Важной областью применения несобственных интегралов в автоматике является построение переходных процессов в САУ. Это является завершающим этапом исследования системы, позволяющим определить основные параметры качества управления и их соответствие нормам технического задания. Основным путем получения кривых переходного процесса систем автоматического управления в настоящее время является применение ЭВМ. Другие методы (аналитические и графические) построения переходных процессов являются вспомогательными и применяются в случае простых систем, а также на этапе предварительного исследования при существенном упрощении системы. Как известно из курса теории автоматического управления переходная функция h(t) связана с действительной и мнимой частями передаточной функции Wз(jw)=Uз(w)+jVз(w) следующими соотношениями:
Uз(0) представляет собой значение h(µ). Если ранее, ввиду ограниченных вычислительных возможностей, для нахождения этого интеграла использовался метод нормированных трапеций, предложенный В.В. Солодовниковым для построения переходной функции по вещественной части Uз(w) , то в настоящее время переходной процесс может быть построен прямым численным интегрированием по приведенным выше формулам. Для этого вначале необходимо провести преобразование передаточной функции замкнутой системы, выделив из неё в явном виде действительную часть и подставить это выражение в одну из рассматриваемых далее программ. При этом устраняется необходимость в графическом построении вещественной части АЧХ. Двойные (кратные)интегралы вида
могут вычисляться по кубатурной формуле Симпсона. При этом область интегрирования на плоскости XOY разбивается на четыре квадрата и значение интеграла I вычисляется по формуле:
Кубатурная формула Гаусса с n=2 имеет вид:
Сложная кубатурная формула Гаусса реализуется разбивкой отрезков [a,b] и [c,d] на М и N частей с последующим применением предыдущей формулы к этим частям. При этом повышается точность вычислений. Примеры программной реализации рассмотренных методов Метод Симпсона 01 cls 05 Print "Численное интегрирование по методу Симпсона" 10 Input "Введите нижний предел интегрирования A=",a 15 Input " Введите верхний предел интегрирования B=",b 20 Input " Введите число интервалов интегрирования M=",m 25 h=(b-a)/m: x=a:gosub 110: i=f 30 for j=1 to m step 2 35 x=a+j*h:gosub 110:if j<m then i=i+4*f 40 next j 60 for j=2 to m step 2 65 x=a+j*h: gosub 110:if j<m then i=i+2*f 70 next j 75 x=b: gosub 110: i=(i+f)*h/3 80 print " Значение интеграла i=";i 90 end 100 rem задание подынтегральной функции 110 f=sqr(2*x+1): return
Метод Боде 01 cls 05 Print "Численное интегрирование по методу Боде" 10 Input "Введите нижний предел интегрирования A=",a 15 Input " Введите верхний предел интегрирования B=",b 20 Input " Введите число интервалов интегрирования M=",m 25 h=(b-a)/m: e=h/4:x=a 30 gosub 110 35 i=7*f 40 for n=1 to m 45 x=x+e 50 gosub 110:i=i+32*f:x=x+e 55 gosub 110:i=i+12*f:x=x+e 60 gosub 110:i=i+32*f:x=x+e 65 gosub 110:i=i+14*f 70 next n 75 i=i-7*f: i=i*2*e/45 80 print " Значение интеграла i=";i 90 end 100 rem задание подынтегральной функции 110 f=sqr(2*x+1): return Метод Уэддля 01 cls 05 Print "Численное интегрирование методом Уэддля" 10 Input "Введите нижний предел интегрирования A=",q 15 Input " Введите верхний предел интегрирования B=",b 20 Input " Введите число интервалов интегрирования M=",m 25 a=q:h=(b-a)/m:x=a:gosub 110 30 i=f:l=h/6 35 for e=1 to m 45 x=x+l:gosub 110:i=i+5*f 50 x=x+l:gosub 110:i=i+f 55 x=x+l:gosub 110:i=i+6*f 60 x=x+l:gosub 110:i=i+f 65 x=x+l:gosub 110:i=i+5*f 70 x=x+l:gosub 110:i=i+2*f 75 a=x 80 next e 85 i=(i-f)*3*l/10 90 print "i=";i 95 end 100 rem задание подынтегральной функции 110 f=sqr(2*x+1): return
Метод Чебышева 01 cls 05 Print "Численное интегрирование по методу Чебышева" 10 Input "Введите нижний предел интегрирования A=",q 15 Input " Введите верхний предел интегрирования B=",b 20 Input " Введите число интервалов интегрирования M=",m 25 a=q:t=sqr(2)/2:i=0:h=(b-a)/m 35 for e=1 to m 37 w=a+h:c=(w+a)/2:d=(w-a)/2:x=c-d*t 40 gosub 110:i=i+f:x=c 45 gosub 110:i=i+f:x=x+d*t 50 gosub 110:i=i+f:a=w 55 next e 85 i=i*h/3 90 print " Значение интеграла i=";i 95 end 100 rem задание подынтегральной функции 110 f=sqr(2*x+1): return
Метод Гаусса 01 cls 05 Print "Численное интегрирование по методу Гаусса" 10 Input "Введите нижний предел интегрирования A=",q 15 Input " Введите верхний предел интегрирования B=",b 20 Input " Введите число интервалов интегрирования M=",m 25 a=q:t=sqr(0.6):i=0:h=(b-a)/m 35 for e=1 to m 37 b1=a+h:c=(b1+a)/2:d=(b1-a)/2:x=c-d*t 40 gosub 110:y=d*5*f/9:i=i+y:x=c 45 gosub 110:y=d*8*f/9:i=i+y:x=c+d*t 50 gosub 110:y=d*5*f/9:i=i+y:a=b1 55 next e 90 print "i=";i 95 end 100 rem задание подынтегральной функции 110 f=sqr(2*x+1): return 12 |
(5.3)
. (5.4)
(5.5)
. (5.6)
. (5.7)
(5.8)
. Таким образом, погрешность формулы (5.7) пропорциональна O(h2).
. (5.9)
, (5.10)
(5.11)
(5.12)
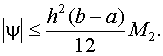(5.13)
(5.14)
(5.15)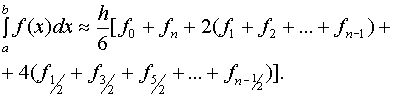
(5.16)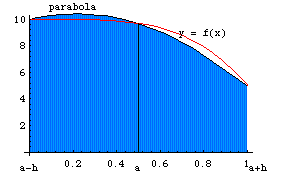
(5.17)
(5.18)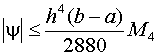
, (5.19)
. Таким образом, погрешность формулы Симпсона пропорциональна O(h4).
с пределом интегрирования a и b можно трактовать как площадь фигуры, ограниченной вертикальными линиями в точках a и b, осью абсцисс и графиком подынтегральной функции f(x) . Аналитическое вычисление определенного интеграла для которого известна его первообразная F(x) производится по формуле Ньютона-Лейбница 
. Поэтому для вычисления определенного интеграла достаточно вычислить значения F(x) для пределов интегрирования. Если же нахождение вида первообразной сложно или невозможно, то применяется численное интегрирование. Оно заключается в аппроксимации f(x) на отрезке [a, b] некоторой более простой функцией, для которой определенный интеграл легко подсчитывается по формулам численного интегрирования. Обычно отрезок [a, b] разбивается на m частей, к каждой из которых применяется соответствующая простая формула. Таким образом получают составные формулы численного интегрирования.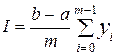
,
.
.
, где
,где
Для повышения точности интегрирования область интегрирования может быть разбита на несколько квадратов для каждого из которых проводятся аналогичные вычисления.
где P=(b-a)/2, R=(d-c)/2, .а узлы интерполяции расположены на расстоянии 
±KP и ±KR от осей, где К=Ö(1/3).