 ПОЗНАВАТЕЛЬНОЕ
| Вычисление несобственного интеграла 12
01 cls 03 defdbl a-z 05 print " Вычисление несобственного интеграла с бесконечным верхним пределом с заданной точностью методом Гаусса" 10 input " введите нижний предел интегрирования a=",q 15 input " введите начальное приближение верхнего предела b0=",z 20 input " введите погрешность результата e=",n 25 m=1:k=0:b=z/2:t=sqr(0.6):u=0 30 b=b*2 35 m=m*2:a=q:i=0:h=(b-a)/m 40 for j=1 to m 45 c=a+h/2: d=h/2 50 e=d*5/9:l=d*8/9:d=d*t 55 x=c-d: gosub 150 60 i=i+e*f 65 x=c: gosub 150: 70 i=i+l*f 75 x=c+d: gosub 150 80 i=i+e*f 85 a=a+h 90 next j 95 l=k 100 k=i 105 if abs(i-l)>n*30 then goto 35 110 v=u:u=1 115 if abs(i-v)>n/2 then goto 30 120 print " Значение интеграла i=";i 130 end 140 rem задание подинтегральной функции 150 f=x*exp(-x): return
Вычисление двойного интеграла Методом Симпсона 01 cls 03 defdbl a-z 05 print " Вычисление двойного интеграла по простой формуле Симпсона" 10 input "Введите пределы интегрирования a,b,c,d ",a,b,c,d 20 s=0:h=(b-a)/2:k=(d-c)/2 25 x=a:y=c: gosub 140 30 s=s+f 35 x=b: gosub 140 40 s=s+f 45 x=a:y=d:gosub 140: s=s+f 50 x=b:gosub 140:s=s+f 55 x=a+h:y=c:gosub 140:s=s+4*f 60 y=d:gosub 140:s=s+4*f 65 x=a:y=c+k:gosub 140:s=s+4*f 70 x=b:gosub 140:s=S+4*f 75 x=a+h:gosub 140:s=s+16*f 80 i=s*h*k/9 85 print " Значение интеграла i=";i 90 end rem задание подынтегральной функции 140 1/(x*y):return
Методом Гаусса 01 cls 03 defdbl a-z 05 print " Вычисление двойного интеграла простым методом Гаусса" 10 s=0 15 input " Введите пределы интегрирования a,b,c,d ",a,b,c,d 20 o=(a+b)/2:p=(b-a)/2:q=(c+d)/2 25 r=(d-c)/2:k=sqr(1/3) 30 x=o+p*k:y=q+r*k:gosub 100 35 x=o-p*k:gosub 100 40 y=q-r*k: gosub 100 45 x=o+p*k:gosub 100 50 i=s*r*p 55 print " Значение интеграла i=";i 60 end 90 rem задание подынтегральной функции 100 f=1/(x*y):s=s+f:return
Методом Гаусса с повышенной точностью 01 cls 03 defdbl a-z 05 print " Вычисление двойного интеграла по методу Гаусса с повышенной точностью" 10 s=0 15 input " Введите пределы интегрирования a,b,c,d ",w,b,c,d 20 input " Введите количество интервалов разбиения m,n ",m,n 23 h=(b-w)/m:l=(d-c)/n:k=sqr(1/3) 25 for i=1 to n 27 q=(c+d)/2:r=l/2:a=w 29 for j=1 to m 32 b=a+h:o=(a+b)/2:p=h/2 30 x=o+p*k:y=q+r*k:gosub 100 35 x=o-p*k:gosub 100 40 y=q-r*k: gosub 100 45 x=o+p*k:gosub 100 50 a=b 55 next j 60 next i 65 i=s*h*l/4 70 print " Значение интеграла i=";i 75 end 90 rem задание подынтегральной функции 100 f=1/(x*y):s=s+f:return Программы для методов прямоугольников и трапеций необходимо разработать самостоятельно на основе анализа приводимых выше примеров и рассмотренного ранее теоретического описания! Задания для выполнения.
1.Вычислить приближенно методом прямоугольников и Симпсона следующий интеграл: Ответ: 1,398717474 2. Вычислить приближенно следующими методами с шагом h=1 интеграл a) правых прямоугольников, b) левых прямоугольников, c) центральных прямоугольников, d) трапеций, e) Симпсона.
5.Контрольные вопросы. 1. Пояснить получение простейших формул численного интегрирования (формулы правых, левых, центральных прямоугольников, формула трапеций, формула Симпсона), 2. Геометрическая иллюстрация, оценки погрешности простейших формул численного интегрирования.
6. Рекомендуемая литература
1. Тарасевич Ю. Ю. Математическое и компьютерное моделирование. –М.: Едиториал УРСС. 2001. – 144 с. 2. Самарский А.А., Михайлов А.П. Математическое моделирование: Идеи. Методы. Примеры. – М.: Физматлит, 2001. – 320 с. 3. Советов Б.Я., Яковлев С.А. Моделирование систем. – М.: Высш. шк., 1998. – 320 с. 4. Липай Б.Р., Маслов С.И. Компьютерное моделирование электромеха-нических систем: Учеб. пос. – М.: Изд. МЭИ, 2002. – 80 с. 5. Дьяконов В. Matlab 6: Учебный курс -СПб.: Питер, 2001. - 592 с. 6. Дьяконов В., Круглов В. Математические пакеты расширения Matlab. Специальный справочник. – Спб.: Питер, 2001. – 480 с. 7. Введение в математическое моделирование: Учебное пособие/ Ашихмин В.Н., Гитман М.Б., Келлер И.Э., Наймарк О.Б. и др.// М.: Логос, 2004. 8. Могилёв А.В., Пак Н.И., Хённер Е.К. Информатика.М.,ACADEMA, 2007. 9. Могилёв А.В., Пак Н.И., Хённер Е.К. Практикум по информатике. М.,ACADEMA,2007.
12 |



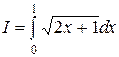
 и сравнить точность методов:
и сравнить точность методов: