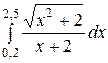 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Простейшие квадратурные формулы 12
Формулы прямоугольников.Как известно, определенный интеграл в силу своего построения есть предел интегральных сумм:
каждая, из которых соответствует некоторому разбиению Ограничиваясь конечным числом слагаемых в правой части равенства (22) и принимая в качестве набора
Пример 1: С помощью формул левых и правых прямоугольников вычислить Зная приделы интегрирования a = 1 и b = 9, находим шаг
Если вычисление определенного интеграла произвести по формуле (24), то получим:
Наиболее часто используемой формулой, основанной на идее представления определенного интеграла в виде интегральной суммы, является формула прямоугольников, где в качестве
где Выражение для остаточного члена квадратурной формулы (25):
Таким образом, оценку погрешности квадратурной формулы (25) можно представить в следующем виде:
где Суммарная вычислительная погрешность
Эта погрешность не зависит от числа разбиений отрезка интегрирования, а пропорциональна только его длине. Пример 2: Вычислить с помощью формулы прямоугольников интеграл По заданным пределам интегрирования и числу разбиений n определим шаг:
Вычислив необходимые значения функции с тремя верными в узком смысле знаками
Погрешность метода оценим по формуле (27), для чего предварительно найдем максимум абсолютной величины второй производной подынтегральной функции:
Таким образом, погрешность метода есть
Пользуясь формулой (28), найдем вычислительную погрешность:
Следовательно за полную погрешность приближенного вычисления интеграла можно принять Формула трапеций.Перейдем теперь к другому способу построения квадратурных формул, связанному с аппроксимацией подынтегральной функции интерполяционным многочленом. Рассмотрим простейший случай аппроксимации многочленом первой степени с узлами в точках a и b:
Интегрируя правую и левую части этого равенства и используя вторую теорему о среднем значении функции при интегрировании последнего слагаемого правой части, находим:
Таким образом, предполагая, что отрезок интегрирования мал, получаем квадратурную формулу, называемую формулой трапеций:
с остаточным членом
Используя выражение (27) для остаточного члена, опенку погрешности квадратурной формулы (29) можно представить в виде
где Полученные выражения для остаточного члена (30) и погрешности (31) показывают, что квадратурная формула (29) является точной для всех линейных функций, поскольку вторая производная таких функций равна нулю, а, следовательно, равны пулю остаточный член и погрешность. Пример 3: Вычислить с помощью формулы трапеций интеграл На основании формулы (29) имеем
Вычислив необходимые значения функции, получим
Погрешность метода оценим по формуле (31), используя значение М=2:
Вычислительная погрешность, очевидно, равна нулю, так как значения функции и Итак, окончательно имеем Отметим, что в примере 3 получилось гораздо менее точное решение, чем в примере 2. Однако использование в примере 3 формулы трапеций имеет свои преимущества. Во-первых, если подынтегральная функция задана в виде таблицы ее значений в узлах Ценность квадратурной формулы определяется не только формой ее остаточного члена (или погрешности), но и другими факторами, например временем счета. 3. Объекты исследования, оборудование, материалы и наглядные пособия Объектом исследования данной лабораторной работы являются система линейных алгебраических уравнений и методы ее численного решения. Для выполнения работы необходимы ПК и соответствующее программное обеспечение: - MS WINDOWS; - Delphi (любая другая оболочка языка высокого уровня); - MS Office (для оформления отчета).
4. Задание на работу (рабочее задание) Разработать программное обеспечение для численного расчета: 1) Первой и второй производных функции, заданной таблично; 2) с помощью формул левых, правых, центральных прямоугольников и формулы трапеции определенного интеграла.
Варианты:
12 |
, (22)
: 
отрезка 
и произвольному набору точек 
для каждого разбиения; 
.
те или иные значения аргумента из отрезков 
, можно получить различные формы приближенного интегрирования. Так, принимая в качестве набора 
:
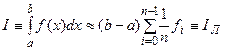, (23)
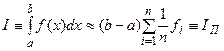. (24)
, полагая n = 4.
; тогда точками разбиения служат 
, 
, 
, 
, 
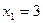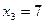, а значения подынтегральной функции 
в этих точках таковы:
Далее найдем числовое значение интеграла, пользуясь формулой (23):
эта формула имеет следующий вид:
, (25)
; 
; 
.
(26)
(27)
составит
(28)
, полагая n = 4. Оценить погрешность полученного приближенного значения.
. далее на основании формулы (25) имеем
, получим
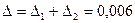, а окончательный ответ записать в виде 
Для сравнения приведем несколько знаков точного значения вычислительного интеграла: 
.
; 
.
; 
.
(29)
; 
, (31)
.
.
.
.
, найдены абсолютно точно.
.
, то для использования формулы прямоугольников необходимо определить значения этой функции еще и в точках 
, что вносит дополнительные трудности и дополнительную погрешность. Во-вторых, в примере 3 значения подынтегральной функции были вычислены всего лишь в двух точках, в то время как в примере 2 - в четырех точках, что, естественно, потребовало большего времени.
