 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Постановка задачи численного дифференцирования и простейшие формулы численного дифференцирования 12
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение Высшего профессионального образования «Тульский государственный университет»
Политехнический институт
Кафедра "Автоматизированные станочные системы"
Методические указания к Лабораторной работе № 4 ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ
по дисциплине «ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА»
Направление подготовки: 230100 – «Информатика и вычислительная техника» Специальность: 230104 «Системы автоматизированного проектирования» Форма обучения: очная
Тула 2012
Методические указания к лабораторным работам составлены профессором Ямниковой О.А. и обсуждены на заседании кафедры «Автоматизированные станочные системы» механико-технологического факультета
протокол №1 от "31" августа 2011 г.
Зав. кафедрой ________________________ А.Н. Иноземцев
Методические указания к лабораторным работам пересмотрены и утверждены на заседании кафедры «Автоматизированные станочные системы» механико-технологического факультета
протокол №1 от "____" ___________20___ г.
Зав. кафедрой ________________________ А.Н. Иноземцев
1. Цель и задачи работы
Получить навык - построения расчетной интерполяционной формулы для нахождения производной и вычисления определенного интеграла функции, заданной таблично; - разработки программных средств для дифференцирования и интегрирования функции, заданной таблично. Теоретические положения
Постановка задачи численного дифференцирования и простейшие формулы численного дифференцирования Простейшие выражения для производных получаются в результате дифференцирования интерполяционных форм. Рассмотрим следующую задачу. На сетке Один из возможных способов решения этой задачи заключается в следующем. Построим для функции f по узлам
Продифференцируем правую и левую части соотношения (1) m раз и положим
Для достаточно гладких функций, т.е. для функций с ограниченными производными, необходимым количеством узлов и заданной точностью величиной, величина
Остановимся более подробно на получении расчетных формул для
Дифференцируя многочлен Стирлинга два раза по x и вычисляя значение второй производной в точке
Для вычисления производной точно в середине между узлами
Практический интерес представляют также так называемые формулы одностороннего дифференцирования, позволяющие вычислить Дифференцируя первый многочлен Ньютона по x и вычисляя значение производной в точке
Из соотношений (4), (6) и (8) имеем
Соотношения (11) и (13) соответственно дают
Пример. Вычислить Таблица
На основании формул (17) и (19) получаем:
12 |



 в узлах
в узлах  заданы значения
заданы значения  функции f, непрерывно дифференцируемой n+m+1 раз. Требуется вычислить производную
функции f, непрерывно дифференцируемой n+m+1 раз. Требуется вычислить производную  и оценить погрешность.
и оценить погрешность. интерполяционный многочлен с остаточным членом
интерполяционный многочлен с остаточным членом 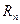 , так что
, так что . (1)
. (1) :
: . (2)
. (2) мала и
мала и  является хорошим приближенным для
является хорошим приближенным для  , так что можно положить
, так что можно положить . (3)
. (3)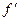 и
и  в узлах равномерной сетки. Для получения производных в узловых точках целесообразно использовать интерполяционный многочлен Стирлинга и его остаточный член. Так дифференцируя многочлен Стирлинга и его остаточный член по x и полагая
в узлах равномерной сетки. Для получения производных в узловых точках целесообразно использовать интерполяционный многочлен Стирлинга и его остаточный член. Так дифференцируя многочлен Стирлинга и его остаточный член по x и полагая  (
(  ), получим следующие выражения для производной:
), получим следующие выражения для производной: (k=1) (4)
(k=1) (4) (k=2) (5)
(k=2) (5) (k=1) (6)
(k=1) (6) (k=2) (7)
(k=2) (7)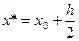 применяют многочлен Бесселя. В этом случае соответствующие формулы для производной имеют вид
применяют многочлен Бесселя. В этом случае соответствующие формулы для производной имеют вид (k=1) (8)
(k=1) (8) (k=2) (9)
(k=2) (9) по узлам
по узлам  (i=0,1,…,k,… или i=0,- 1,…,- k,…). Построение этих формул удобно провести с помощью первого и второго интерполяционных многочленов Ньютона.
(i=0,1,…,k,… или i=0,- 1,…,- k,…). Построение этих формул удобно провести с помощью первого и второго интерполяционных многочленов Ньютона. (t = 0) для k=1 и k=2 получим соответственно следующие формулы:
(t = 0) для k=1 и k=2 получим соответственно следующие формулы: (10)
(10) (11)
(11) (14)
(14) (15)
(15) (16)
(16) (17)
(17) (18)
(18) ,
, 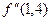 для функции f(x), заданной в виде таблицы.
для функции f(x), заданной в виде таблицы.