 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Динамика объектов. Динамические характеристики 12
Динамика изучает поведение объектов в неустановившихся (переходных) режимах. Неустановившийся режим автоматических систем возникает при нарушении равновесия между притоком и стоком (приходом и расходом) вещества, энергии или количества движения в любом звене. Он характеризуется изменением параметров звена и системы во времени . Динамические характеристики объектов отражают их реакцию на возмущения того или иного рода. Наиболее часто определяется реакция на типовые воздействия: а - ступенчатая (единичная) функция, б-прямоугольный импульс, в - прямоугольная волна, г -гармонические колебания, рис.2.5. Реакция объекта на ступенчатое (скачкообразное) воздействие называется переходной функцией (характеристикой).Часто это воздействие называют единичным, принимая изменение входной величины х в нулевой (начальный) момент времени, равным единице. Переходные функции широко используются для наглядного представления динамических свойств объектов.
Когда продолжительное отклонение входной величины от установившегося значения недопустимо по условиям работы объекта, рассматривают реакцию его на прямоугольный импульс. Она менее наглядна, но содержит всю информацию о динамических свойствах объекта. При аналитическом исследовании нередко используют импульсное воздействие 1(т), при котором в бесконечно малый промежуток времени на объект действует бесконечно большое по амплитуде возмущение с суммарным (интегральным) эффектом, равным единице. Подача прямоугольной волны на вход объекта позволяет избежать продолжительного отклонения выходной величины в одну сторону. Проявляются лишь небольшие отклонения ее в обе стороны, но они по-прежнему содержат полную информацию о динамических свойствах объекта. Гармонические колебания применяются для определения частотных характеристик объектов. При определении динамических характеристик объектов часто рассматривают лишь отклонения параметров от начальных установившихся значений, принимая последние равными нулю. Такой подход означает условное разделение нестационарного режима на установившийся режим и переходный процесс. Он вполне оправдан, если в переходном процессе изменения входных и выходных величин не превышают значений, при которых начинает заметно сказываться нелинейность объекта. Реальные промышленные объекты допускают накопление вещества, энергии или количества движения в нескольких аккумулирующих емкостях, между которыми имеются какие-то сопротивления. Подобные объекты называют многоемкостными. Характерной особенностью их является искривление начального участка переходной функции, т.е. замедленное изменение выходной величины в начале переходного процесса, рис.2.6. В объектах с самовыравниванием при ступенчатом входном воздействии выходная величина у с течением времени стремится к новому установившемуся значению, кривая 1. Выходная величина объектов без самовыравнивания при таком же воздействии по прошествии начального периода изменяется с постоянной скоростью, кривая 2. Для простых одноемкостных объектов без самовыравнивания постоянная скорость изменения выходной величины наступает сразу после нанесения ступенчатого воздействия
Динамические характеристики объектов могут быть определены как экспериментально, так и аналитически. Наиболее достоверные данные получаются на основе эксперимента, постановка которого требует значительных затрат времени и средств. Для сравнительно простых объектов, процессы в которых хорошо изучены, динамические характеристики определяют аналитически. Независимо от способа получения исходной информации для решения практических задач используются математические модели объектов, представленные в виде уравнений динамики. Уравнения динамики При аналитическом определении характеристик уравнения динамики объектов составляются по принципу: Приход - Расход = Скорость накопления. Этому принципу соответствуют законы сохранения вещества, энергии и количества движения. По существу, составление уравнений динамики заключается в последовательном применении указанных законов к каждой аккумулирующей емкости с учетом термических, гидравлических и иных сопротивлений. Для упрощения задачи обычно вводят те или иные допущения, т.к. реальный объект всегда сложнее любой математический модели. Рассмотрим два простейших примера. 1.Сосуд, жидкость из которого откачивается насосом, является астатическим объектом, если объемные расходы на притоке Vn и оттоке V0 не зависят от уровня /г, рис.2.7 а. Предполагается, что жидкость однородная, сосуд открытый и находится при атмосферном давлении, изменения уровня в нем практически не влияют на производительность насоса. Данный объект имеет ояну аккумулирующую емкость. В соответствии с общим принципом записываем уравнение материального баланса:
При постоянной по высоте площади сечения сосуда F объем жидкости пропорционален ее уровню: (2.9) Если сосуд где vn, клонения расходов от установившихся значений. Полагая, что производительность насоса остается постоянной, после подстановки
Задаваясь несколькими значениями времени от начала переходного процесса строим переходную функцию, рис.2.7 б. Если ступенчато возрастает производительность насоса или уменьшается расход поступающей жидкости, то уровень снижается с постоянной скоростью, как показано пунктирной линией. Угол наклона на графике переходной функции зависит от значения ДК/F. Характерной особенностью является накопление жидкости, пропорциональное времени от начала переходного процесса. Подобные объекты относятся к интегрирующим. , относится к статическим объектам, рис.2.8 а. Дело в том, что расход вытекающей через патрубок или отверстие жидкости V0 зависит от ее уровня, рис.2.8 б. Эта зависимость близка к линейной. По крайней мере вблизи установившихся значений справедливо выражение:
где К] - коэффициент пропорциональности. Величину коэффициента К\ можно найти по графику упомянутой зависимости как тангенс угла наклона прямого участка вблизи рассматриваемой точки. Можно воспользоваться также отношением небольших приращений: K\=&.Vn Ih. Отсюда легко найти размерность коэффициента К\. Исходное уравнение динамики имеет прежний вид:
Нетрудно убедиться, что множитель при производной имеет размерность времени. Его называют постоянной времени и обозначают буквой T=F/Ki. Обозначив также К=1/К/, получим: (2.14) Решение
Задаваясь рядом значений текущего времени т, по этому выражению строим график переходной функции. Он имеет вид экспоненты, рис.2.8 в. С течением времени уровень жидкости приходит к новому установившемуся значению. Чтобы определить отклонение уровня в конце переходного процесса Ahic необязательно строить график. Достаточно в уравнении (2.14) производную приравнять нулю. Чем меньше постоянная времени Т, тем быстрее наступает новое состояние равновесия. Она является мерой инерционности
объекта. Подобные объекты считаются инерционными или апериодическими. 12 |
(2.8) те и - объем жидкости в сосуде.
имеет неодинаковую форму по высоте, то последнее выражение получается более сложным. Рассматривая малые отклонения уровня, даже при любой форме сосуда в первом приближении используют линейную зависимость (2.9). Расходы поступающей и откачиваемой жидкости являются независимыми параметрами. Их можно представить в виде двух слагаемых:
Vo - значения расходов в установившемся режиме; ДК„, ДК„ - от_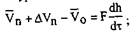
в уравнение (2.8) имеем:
(2.12)
данного дифференциального уравнения при нулевых на- . чальных условиях и ступенчатом входном воздействии по методу Эйлера принимает вид:
(2-15)